![\[ R_0 = f, R_1 = g, R_2, \ldots \ldots, R_N \]](form_90.png)
![$f (x), g (x) \in \mathbbm{K}[x]$](form_89.png) are sequences of polynomials defined as follows
are sequences of polynomials defined as follows
![\[ R_0 = f, R_1 = g, R_2, \ldots \ldots, R_N \]](form_90.png)
such that 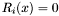 implies that for the first term such that
implies that for the first term such that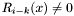 and
and 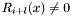 , we have
, we have 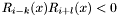 , we. One can chose for instance
, we. One can chose for instance
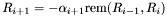
where 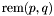 is the remainder in the Euclidean division of a polynomial
is the remainder in the Euclidean division of a polynomial 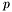 by
by 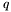 , and
, and 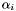 is a positive number.
is a positive number.
template<class C, class UPOL=UPolDse<C>, class SEQ=std::vector<UPOL> > SturmSeq
C, the type of coefficients of the polynomialsUPOL, the type of univariate polynomials. The default value is UPolDse<C>.SEQ, the type of the container used to store the sequence. The default value is std::vector<UPOL>.Here is an example of construction of a Sturm Habicht sequence of two polynomials:
UPolDse<ZZ> p,q; SturmSeq<ZZ> s(p,q,HABICHT());
synaps/upol/SturmSeq.hint variation(const SturmSeq<C,UPOL,S>& s, const R& x)
s at the value x.R.UPOLDAR::sign_at.![]()
![]()
#include <synaps/arithm/gmp.h> #include <synaps/upol.h> #include <synaps/upol/SturmSeq.h> typedef UPolDse<ZZ> upol_t; int main(int argc, char** argv) { upol_t p("x^3-234234*x^2+32332334554*x-12221118723"); SturmSeq<ZZ> s(p,diff(p),HABICHT()); std::cout<<s<<std::endl; //| [1*x^3-234234*x^2334554*x-12221118723,3*x^2-468468*x+334554, //| 109729126188*x+31626146871,-628213673160260696955282507] std::cout <<"Number of positive root(s): " <<variation(s,0)-variation(s,Infinity(1))<<std::endl; //| Number of positive root: 1 std::cout <<"Number of negative root(s): " <<variation(s,Infinity(-1))-variation(s,0)<<std::endl; //| Number of negative root: 0 }
 |