Structured matrices are parameterised by the internal representation:
template<class R> struct MatrStr<R>;
Structured matrices are two-dimensional arrays which can be represented by 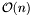 values, where
values, where 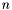 is the size of the matrix. This class provides classical arithmetic operations such as addition, substraction, multiplication by scalars, vectors, matrices . . . The product of two structured matrices is usually not a structured matrices (at least of the same type) and therefore is not implemented. The product of a structured matrices by a vector can usually be performed in almost linear time, ie. in
is the size of the matrix. This class provides classical arithmetic operations such as addition, substraction, multiplication by scalars, vectors, matrices . . . The product of two structured matrices is usually not a structured matrices (at least of the same type) and therefore is not implemented. The product of a structured matrices by a vector can usually be performed in almost linear time, ie. in 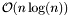 (or
(or 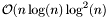 according to the field), using FFT.
according to the field), using FFT.
A matrix 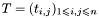 is a Toeplitz matrix if for all
is a Toeplitz matrix if for all 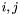 , the entry
, the entry 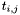 depends only on
depends only on 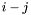 , that is if
, that is if 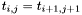 for all pairs of
for all pairs of 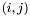 and
and 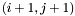 for which the entries
for which the entries 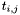 and
and 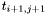 are defined. Associated with a Toeplitz matrix, we have the Toeplitz operator which is a projection composed with the multiplication operator by a univariate polynomial in
are defined. Associated with a Toeplitz matrix, we have the Toeplitz operator which is a projection composed with the multiplication operator by a univariate polynomial in ![$K [x]$](form_78.png) (see [BP94]). An interesting point of this definition is that the product of a
(see [BP94]). An interesting point of this definition is that the product of a 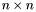 Toeplitz matrix by a vector is a subvector of the coefficient vector of the product of two polynomials of K[x]. This product can be done within
Toeplitz matrix by a vector is a subvector of the coefficient vector of the product of two polynomials of K[x]. This product can be done within 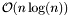 (or
(or 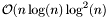 according to the field) operations using FFT.
according to the field) operations using FFT.
An implementation of such data-structure is available as
- See also:
synaps/linalg/toeplitz.h
A matrix 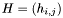 is a Hankel matrix if its entries
is a Hankel matrix if its entries 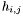 depends only on
depends only on 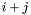 , that is, if
, that is, if 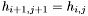 for all pairs
for all pairs 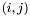 for which the entries are defined. To this kind of matrix, we can associate a Hankel operator which is defined as the projection of the multiplication by a fixed Laurent polynomial (a Laurent polynomial is a polynomial of
for which the entries are defined. To this kind of matrix, we can associate a Hankel operator which is defined as the projection of the multiplication by a fixed Laurent polynomial (a Laurent polynomial is a polynomial of ![$K [x, x^{- 1}]$](form_83.png) , that is a polynomial in both the variables
, that is a polynomial in both the variables 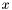 and
and 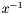 ). So we can compute the product of a
). So we can compute the product of a 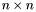 Hankel matrix by a vector as a subvector of the product of a fixed polynomial
Hankel matrix by a vector as a subvector of the product of a fixed polynomial 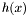 by a polynomial in
by a polynomial in 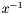 . This can also be done within
. This can also be done within 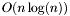 ops (or
ops (or 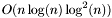 according to the field), using FFT. See [4].
according to the field), using FFT. See [4].
An implementation of such data-structure is available as
- See also:
synaps/linalg/hankel.h
#include <synaps/linalg/MatrStr.H>
#include <synaps/linalg/hankel.H>
typedef MatrStr<linalg::hankel<double> > mstr_t;
int main(int argc, char** argv)
{
double v[]={1,2,1,1,3,4,2,2,5,5,5,5,-2, 1,2,3,1, -2.8,-2.4,1,.2,5.8};
mstr_t A(4,4,v);
std::cout << A << std::endl;
![\[ A \assign \left(\begin{array}{cccc} 1 & 2 & 1 & 1\\ 2 & 1 & 1 & 3\\ 1 & 1 & 3 & 4\\ 1 & 3 & 4 & 5 \end{array}\right) \]](form_88.png)
- See also:
synaps/linalg/MatrStr.h
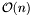 values, where
values, where 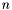 is the size of the matrix. This class provides classical arithmetic operations such as addition, substraction, multiplication by scalars, vectors, matrices . . . The product of two structured matrices is usually not a structured matrices (at least of the same type) and therefore is not implemented. The product of a structured matrices by a vector can usually be performed in almost linear time, ie. in
is the size of the matrix. This class provides classical arithmetic operations such as addition, substraction, multiplication by scalars, vectors, matrices . . . The product of two structured matrices is usually not a structured matrices (at least of the same type) and therefore is not implemented. The product of a structured matrices by a vector can usually be performed in almost linear time, ie. in 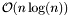 (or
(or 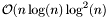 according to the field), using FFT.
according to the field), using FFT.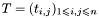 is a Toeplitz matrix if for all
is a Toeplitz matrix if for all 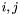 , the entry
, the entry 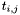 depends only on
depends only on 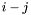 , that is if
, that is if 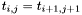 for all pairs of
for all pairs of 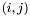 and
and 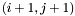 for which the entries
for which the entries 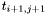 are defined. Associated with a Toeplitz matrix, we have the Toeplitz operator which is a projection composed with the multiplication operator by a univariate polynomial in
are defined. Associated with a Toeplitz matrix, we have the Toeplitz operator which is a projection composed with the multiplication operator by a univariate polynomial in ![$K [x]$](form_78.png) (see [BP94]). An interesting point of this definition is that the product of a
(see [BP94]). An interesting point of this definition is that the product of a 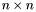 Toeplitz matrix by a vector is a subvector of the coefficient vector of the product of two polynomials of K[x]. This product can be done within
Toeplitz matrix by a vector is a subvector of the coefficient vector of the product of two polynomials of K[x]. This product can be done within 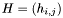 is a Hankel matrix if its entries
is a Hankel matrix if its entries 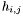 depends only on
depends only on 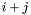 , that is, if
, that is, if 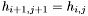 for all pairs
for all pairs ![$K [x, x^{- 1}]$](form_83.png) , that is a polynomial in both the variables
, that is a polynomial in both the variables 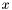 and
and 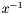 ). So we can compute the product of a
). So we can compute the product of a 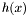 by a polynomial in
by a polynomial in 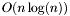 ops (or
ops (or 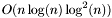 according to the field), using FFT. See [4].
according to the field), using FFT. See [4].![\[ A \assign \left(\begin{array}{cccc} 1 & 2 & 1 & 1\\ 2 & 1 & 1 & 3\\ 1 & 1 & 3 & 4\\ 1 & 3 & 4 & 5 \end{array}\right) \]](form_88.png)
