![\[ \left\{ \begin{array}{l} f_0 (\mathbf{x}, \mathbf{c}) = \sum_{j = 0}^{k_0} c_{0, j} \psi_{0, j} (\mathbf{x})\\ \vdots\\ f_n (\mathbf{x}, \mathbf{c}) = \sum_{j = 0}^{k_n} c_{n, j} \psi_{n, j} (\mathbf{x}) \end{array} \right. \]](form_210.png)
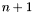 generic polynomials:
generic polynomials:
![\[ \left\{ \begin{array}{l} f_0 (\mathbf{x}, \mathbf{c}) = \sum_{j = 0}^{k_0} c_{0, j} \psi_{0, j} (\mathbf{x})\\ \vdots\\ f_n (\mathbf{x}, \mathbf{c}) = \sum_{j = 0}^{k_n} c_{n, j} \psi_{n, j} (\mathbf{x}) \end{array} \right. \]](form_210.png)
where
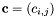 are the parameters,
are the parameters,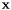 is a point of the variety
is a point of the variety 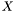 of dimension,
of dimension,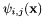 are polynomial functions on
are polynomial functions on 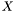 .
.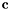 , such that this system has a root in
, such that this system has a root in 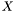 . In the case, we are considering, there exists a polynomial
. In the case, we are considering, there exists a polynomial 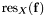 in the parameters {{c}}, such that
in the parameters {{c}}, such that
![\[ \tmop{res}_X (\mathbf{f}) = 0 \]](form_217.png)
iff the previous system has a solution in 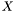 . This polynomial is called the resultant of
. This polynomial is called the resultant of 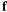 on
on 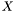 . Different constructions of resultants are presented hereafter.
. Different constructions of resultants are presented hereafter.
template<class R,class L,class LM> R matrix_of(const L& l, char t='N'); template<class R,class L,class LM> R matrix_of(const L& l, const LM & lm, char t='N');
The use of such functions is done by specifying the output of matrices:
MAT m = matrix_of<MAT>(l);
MAT m = matrix_of<MAT>(l,'T');
l is a list of multivariate polynomials, MAT the type of output matrix that we want to compute, and 'T' specifies if the transposed matrix is computed.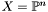 and
and 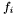 is a generic polynomial of degree
is a generic polynomial of degree 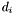 ,
, 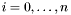 . The construction used is the one described by F.S. Macaulay.
. The construction used is the one described by F.S. Macaulay. MAT m = macaulay<MAT>(l);
MAT mt = macaulay<MAT>(l,'T');
l is a list of 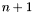 multivariate polynomials in
multivariate polynomials in 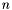 variables,
variables, MAT the type of output matrix that we want to compute, and 'T' specifies if the transposed matrix is computed or not.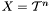 is the toric variety associated to the Minkowsky sum of polytopes
is the toric variety associated to the Minkowsky sum of polytopes 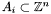 and
and 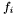 is a generic polynomial of support in
is a generic polynomial of support in 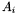 ,
, 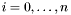 . The construction used is the one described in [CaEm93].
. The construction used is the one described in [CaEm93].
synaps/mpol/Toric.h (affine) polynomials
(affine) polynomials 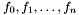 in the variables
in the variables 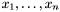 .
.
synaps/mpol/bezoutian.h#include <synaps/mpol.h> #include <synaps/mpol/macaulay.h> #include <synaps/mpol/bezoutian.h> #include <synaps/mpol/Toric.h> typedef MatrDse<double> matr_t; typedef MPol<double> mpol_t; using std::cout; using std::endl; int main () { mpol_t p0("t+x+2*y"), p1("x^2+y^2-1"), p2("y^2+x*y-1"); vector<mpol_t> l; l.push_back(p0); l.push_back(p1); l.push_back(p2); cout<< macaulay<matr_t>(l)<<endl;
cout<< m_bezout<matr_t>(l)<<endl;
cout<< toric<matr_t>(l)<<endl;
}
 |