The methods of this family are based on a test which answers either
- there is no root in the domain,
If we are in the first case, we remove the interval. Otherwise, the interval is splitted into two subintervals, to which we apply the test recursively, until a given precision is reached. Consequently, the remaining sub-domains might contain a root, but not guaranty is provided at this step.
The test implemented in thi exclusion solver uses the function
![\[ \Delta_f (x_0, t) = |f (x_0) | - \sum_{i = 0}^{\deg (f)} \frac{|f^{(k)} (x_0) |}{k!} t^k . \]](form_190.png)
We check that if 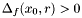 , the interval
, the interval ![$[x_0 - r, x_0 + r]$](form_192.png) does not contain a root of
does not contain a root of 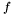 , and thus can be removed. The corresponding function is
, and thus can be removed. The corresponding function is
It returns a sequence of type Seq<C>, where C is the type of the interval bounds a,b.
- See also:
synaps/usolve/Exclusion.h
![\[ \Delta_f (x_0, t) = |f (x_0) | - \sum_{i = 0}^{\deg (f)} \frac{|f^{(k)} (x_0) |}{k!} t^k . \]](form_190.png)
![\[ \Delta_f (x_0, t) = |f (x_0) | - \sum_{i = 0}^{\deg (f)} \frac{|f^{(k)} (x_0) |}{k!} t^k . \]](form_190.png)
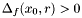 , the interval
, the interval ![$[x_0 - r, x_0 + r]$](form_192.png) does not contain a root of
does not contain a root of 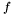 , and thus can be removed. The corresponding function is
, and thus can be removed. The corresponding function is