H. Khalil
This section describes an algorithm, which uses generalized eigenvalues and eigenvectors, for solving a system of two bivariate polynomials 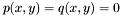 , with
, with ![$p, q \in \mathbb{R} [x, y]$](form_229.png) . It treats multiple roots, which are usually considered as obstacles for numerical linear algebra techniques. The numerical difficulties are handled with the help of singular value decomposition (SVD) of the matrix of eigenvectors associated to each eigenvalue. The extension to
. It treats multiple roots, which are usually considered as obstacles for numerical linear algebra techniques. The numerical difficulties are handled with the help of singular value decomposition (SVD) of the matrix of eigenvectors associated to each eigenvalue. The extension to  equations could be treated similarly.
equations could be treated similarly.
Let 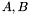 be two square matrices of size
be two square matrices of size 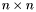 . A {generalized eigenvalue} of
. A {generalized eigenvalue} of 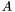 and
and 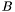 is a value in the set
is a value in the set
![\[ \lambda (A, B) : =\{\lambda \in \mathbb{C} ; \det (A - \lambda B) = 0\}. \]](form_231.png)
A vector 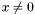 is called a {generalized eigenvector} associated to the eigenvalue
is called a {generalized eigenvector} associated to the eigenvalue 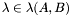 if
if 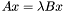 . The matrices
. The matrices 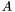 and
and 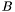 have
have 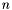 generalized eigenvalues if and only if
generalized eigenvalues if and only if 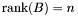 . If
. If 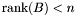 , then
, then 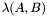 can be finite, empty, or infinite. Note that if
can be finite, empty, or infinite. Note that if 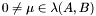 then
then 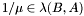 . Moreover, if
. Moreover, if 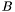 is invertible then
is invertible then 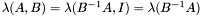 , which is the ordinary spectrum of
, which is the ordinary spectrum of 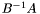 .\
.\
Recall that an 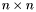 matrix
matrix 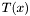 with polynomial coefficients can be equivalently written as a polynomial with
with polynomial coefficients can be equivalently written as a polynomial with 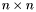 matrix coefficients. If
matrix coefficients. If 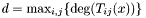 , we obtain
, we obtain 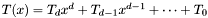 , where
, where 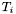 are
are 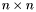 matrices.
matrices.
And we have the following interesting property :
|
Proposition: With the above notation, the following equivalence holds:
![\[ \hspace{1em} T^t (x) v = 0 \Leftrightarrow (A - xB) \left( \begin{array}{c} v\\ xv\\ \vdots\\ x^{d - 1} v \end{array} \right) = 0. \]](form_247.png)
|
From now on we will assume that 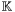 is an algebraically closed field and suppose given two bivariate polynomials
is an algebraically closed field and suppose given two bivariate polynomials  and
and 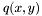 in
in ![$\mathbbm{K} [x, y]$](form_250.png) . Our aim will be to study and compute their common roots. This problem can be interpreted more geometrically. Polynomials
. Our aim will be to study and compute their common roots. This problem can be interpreted more geometrically. Polynomials 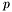 and
and 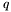 actually define two algebraic curves in the affine plane
actually define two algebraic curves in the affine plane 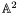 (having coordinates
(having coordinates 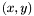 ) and we would like to know their intersection points.
) and we would like to know their intersection points.
Hereafter we will consider systems 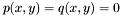 having only a {finite} number of roots. This condition is not quite restrictive since it is sufficient (and necessary) to require that polynomials
having only a {finite} number of roots. This condition is not quite restrictive since it is sufficient (and necessary) to require that polynomials 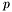 and
and 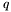 are coprime in
are coprime in ![$\mathbbm{K} [x, y]$](form_250.png) (otherwise one can divide them by their
(otherwise one can divide them by their 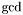 ).
).
In the case where one of the curve is a line, i.e. one of the polynomial has degree 1, the problem is reduced to solving a univariate polynomial. Indeed, one may assume e.g. that 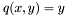 and thus we are looking for the roots of
and thus we are looking for the roots of 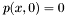 . Let us denote them by
. Let us denote them by 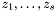 . Then we know that
. Then we know that
![\[ p (x, 0) = c (x - z_1)^{\mu_1} (x - z_2)^{\mu_2} \cdots (x - z_s)^{\mu_s}, \]](form_257.png)
where the 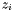 's are assumed to be distinct and
's are assumed to be distinct and 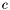 is a non-zero constant in
is a non-zero constant in 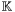 . The integer
. The integer 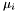 , for all
, for all 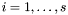 , is called the {multiplicity} of the root
, is called the {multiplicity} of the root 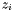 , and it turns out that
, and it turns out that 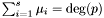 if
if  do not vanish at infinity in the direction of the
do not vanish at infinity in the direction of the 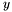 -axis (in other words, if the homogeneous part of
-axis (in other words, if the homogeneous part of 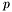 of highest degree do not vanish when
of highest degree do not vanish when 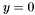 ). This later condition can be avoid in the projective setting: let
). This later condition can be avoid in the projective setting: let 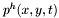 be the homogeneous polynomial obtained by homogenizing
be the homogeneous polynomial obtained by homogenizing  with the new variable
with the new variable 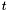 , then we have
, then we have
![\[ p (x, 0, t) = c (x - z_1 t)^{\mu_1} (x - z_2 t)^{\mu_2} \cdots (x - z_s t)^{\mu_s} t^{\mu_{\infty}}, \]](form_267.png)
where 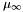 is an integer corresponding to the multiplicity of the root at infinity, and
is an integer corresponding to the multiplicity of the root at infinity, and 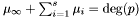 . Moreover, it turns out that the roots
. Moreover, it turns out that the roots 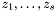 and their corresponding multiplicities can be computed by eigenvalues and eigenvectors computation.
and their corresponding multiplicities can be computed by eigenvalues and eigenvectors computation.
In the sequel we will generalize this approach to the case where 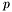 and
and 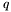 are bivariate polynomials of arbitrary degree. For this we first need to recall the notion of multiplicity in this context. Then we will show how to recover the roots from multiplication maps.
are bivariate polynomials of arbitrary degree. For this we first need to recall the notion of multiplicity in this context. Then we will show how to recover the roots from multiplication maps.
Let 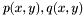 be two coprime polynomials in
be two coprime polynomials in ![$\mathbbm{K} [x, y]$](form_250.png) ,
, 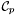 and
and 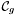 the corresponding algebraic plane curves,
the corresponding algebraic plane curves, 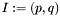 the ideal they generate in
the ideal they generate in ![$\mathbbm{K} [x, y]$](form_250.png) and
and ![$\mathcal{A} : = \mathbbm{K} [x, y] / I$](form_274.png) the associated quotient ring. We denote by
the associated quotient ring. We denote by 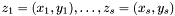 the distinct intersection points in
the distinct intersection points in 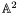 of
of 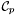 and
and 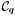 (i.e. the distinct roots of the system
(i.e. the distinct roots of the system 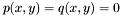 ).
).
A modern definition of the intersection multiplicity of 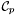 and
and 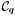 at a point
at a point 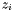 is (see [Ful84])
is (see [Ful84])
![\[ i (z_i, \mathcal{C}_p \cap \mathcal{C}_q) : = \dim_{\mathbbm{K}} \mathcal{A}_{z_i} < \infty, \]](form_277.png)
where the point 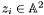 is here abusively (but usually) identified with its corresponding prime ideal in
is here abusively (but usually) identified with its corresponding prime ideal in ![$\mathbbm{K} [x, y]$](form_250.png) ,
, 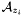 denoting the ordinary localization of the ring
denoting the ordinary localization of the ring 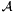 by this prime ideal. As a result, the finite
by this prime ideal. As a result, the finite 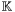 -algebra
-algebra 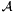 (which is actually finite if and only if
(which is actually finite if and only if  and
and 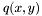 are coprime in
are coprime in ![$\mathbbm{K} [x, y]$](form_250.png) ) can be decomposed as the direct sum
) can be decomposed as the direct sum
![\[ \mathcal{A} = \mathcal{A}_{z_1} \oplus \mathcal{A}_{z_2} \oplus \cdots \oplus \mathcal{A}_{z_s} \]](form_281.png)
and consequently 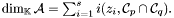
The intersection multiplicities can be computed using a resultant. The main idea is to project ``algebraically'' the intersection points on the 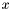 -axis. To do this let us see both polynomials
-axis. To do this let us see both polynomials 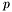 and
and 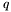 in
in ![$A [y]$](form_283.png) where
where ![$A : = \mathbbm{K} [x]$](form_284.png) , that is to say as univariate polynomials in
, that is to say as univariate polynomials in 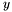 with coefficients in the ring
with coefficients in the ring 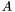 which is a domain; we can rewrite
which is a domain; we can rewrite
![\begin{equation} \label{A[x]} p (x, y) = \sum_{i = 0}^{d_1} a_i (x) y^i, \hspace{.2cm} q (x, y) = \sum_{i = 0}^{d_2} b_i (x) y^i . \end{equation}](form_285.png)
Their resultant (with respect to 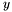 ) is an element in
) is an element in 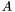 which is non-zero, since
which is non-zero, since 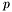 and
and 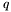 are assumed to be coprime in
are assumed to be coprime in ![$A [y]$](form_283.png) , and which can be factorized, assuming that
, and which can be factorized, assuming that 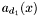 and
and 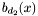 do not vanish simultaneously, as
do not vanish simultaneously, as
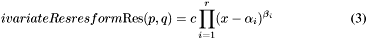
where the 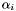 's are distinct elements in
's are distinct elements in 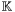 and
and 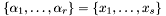 (as sets). For instance, if all the
(as sets). For instance, if all the 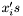 are distinct then we have
are distinct then we have 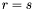 and
and 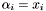 for all
for all 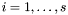 . Moreover, we have (see e.g. [Ful84] (S)):
. Moreover, we have (see e.g. [Ful84] (S)):
Proposition: For all 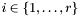 , the integer , the integer 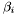 equals the sum of all the intersection multiplicity of equals the sum of all the intersection multiplicity of 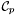 and and 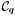 at the points at the points 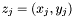 such that such that 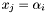 . . |
As a corollary, if all the 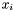 's are distinct (this can be easily obtained by a linear change of coordinates
's are distinct (this can be easily obtained by a linear change of coordinates  ) then
) then 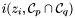 is nothing but the valuation of
is nothing but the valuation of 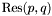 at
at 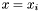 . Another corollary of this result is the well-know Bezout theorem for algebraic plane curves, which is better stated in the projective context. Let us denote by
. Another corollary of this result is the well-know Bezout theorem for algebraic plane curves, which is better stated in the projective context. Let us denote by 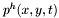 and
and 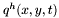 the homogeneous polynomials in
the homogeneous polynomials in ![$\mathbbm{K} [x, y, t]$](form_302.png) obtained from
obtained from 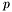 and
and 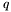 by homogenization with the new variable
by homogenization with the new variable 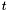 .
.
Proposition: [Bezout theorem] If 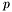 and and 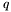 are coprime then the algebraic projective plane curves associated to are coprime then the algebraic projective plane curves associated to 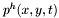 and and 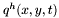 intersect in intersect in 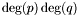 points in points in 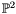 , counted with multiplicities. , counted with multiplicities. |
{proof} It follows straightforwardly from the previous proposition and the well-known fact that 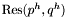 is a homogeneous polynomial in
is a homogeneous polynomial in ![$\mathbbm{K} [x, t]$](form_306.png) of degree
of degree 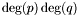 (see e.g. [Lang02], [VWe48II]). {proof}
(see e.g. [Lang02], [VWe48II]). {proof}
We take again the notation of A[x]} and [*] . We denote by  the Sylvester matrix of
the Sylvester matrix of  and
and 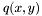 seen in
seen in ![$A [y]$](form_283.png) (assuming that both as degree at least one in
(assuming that both as degree at least one in 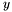 ); thus
); thus 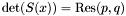 . From [*] , we deduce immediately that
. From [*] , we deduce immediately that 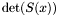 vanishes at a point
vanishes at a point 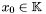 if and only if either there exists
if and only if either there exists 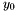 such that
such that 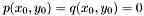 , or either
, or either 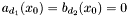 (in which case the intersection point is at infinity). Therefore one may ask the following question : being given a point
(in which case the intersection point is at infinity). Therefore one may ask the following question : being given a point 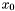 such that
such that 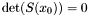 , how to recover all the possible point
, how to recover all the possible point 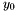 such that
such that 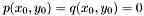 ?
?
Suppose given such a point 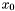 and assume that
and assume that 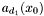 and
and 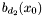 are not both zero. If
are not both zero. If 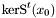 is of dimension one, then it is easy to check that there is only one point
is of dimension one, then it is easy to check that there is only one point 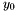 such that
such that 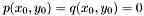 and moreover any element in
and moreover any element in 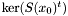 is a multiple of the vector
is a multiple of the vector ![$[1, y_0, \cdots, y_0^{d_1 + d_2 - 1}]$](form_319.png) . Therefore to compute
. Therefore to compute 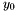 , we only need to compute a basis of
, we only need to compute a basis of 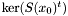 and compute the quotient of its second coordinate by its first one. In case of multiple roots, this construction can be generalized as follows:
and compute the quotient of its second coordinate by its first one. In case of multiple roots, this construction can be generalized as follows:
Proposition: Let 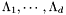 be any basis of the kernel be any basis of the kernel 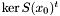 , , 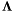 be the matrix whose be the matrix whose 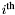 row is the vector row is the vector 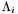 , , 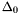 be the be the 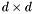 -submatrix of -submatrix of 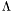 corresponding to the first corresponding to the first 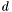 columns and columns and 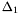 be the be the 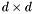 -submatrix of -submatrix of 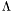 corresponding to the columns number corresponding to the columns number 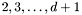 . Then . Then 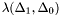 is the set of roots of the equations is the set of roots of the equations 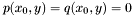 (i.e. the set of (i.e. the set of 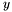 -coordinates of the intersection points of -coordinates of the intersection points of 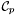 and and 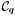 above above 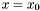 . . |
In this theorem, observe that the construction of 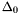 and
and 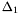 is always possible because we assumed that both polynomials
is always possible because we assumed that both polynomials 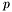 and
and 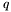 depend on the variable
depend on the variable 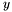 , which implies that the number of rows in the matrix
, which implies that the number of rows in the matrix 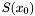 is always strictly greater than the
is always strictly greater than the 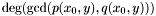 .
.
The previous theorem shows how to recover the 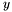 -coordinates of the roots of the system
-coordinates of the roots of the system 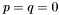 from the Sylvester matrix. However, instead of the Sylvester matrix we can use the Bezout matrix to compute
from the Sylvester matrix. However, instead of the Sylvester matrix we can use the Bezout matrix to compute ![$\tmop{Res} (p, q) \in A [x]$](form_336.png) (see section [*] ). This matrix have all the required properties to replace the Sylvester matrix in all the previous results, except in proposition [*] . Indeed, the Bezout matrix being smaller than the Sylvester matrix, the condition given in remark [*] is not always fulfilled; using Bezout matrix in proposition [*] requires that for all roots
(see section [*] ). This matrix have all the required properties to replace the Sylvester matrix in all the previous results, except in proposition [*] . Indeed, the Bezout matrix being smaller than the Sylvester matrix, the condition given in remark [*] is not always fulfilled; using Bezout matrix in proposition [*] requires that for all roots 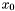 of
of 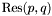 ,
,
![\[ \max (\deg (p (x_0, y), \deg (q (x_0, y)) > \deg (\gcd (p (x_0, y), q (x_0, y)) . \]](form_337.png)
This condition may failed: take for instance 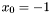 in the system
in the system
![\[ \left\{ \begin{array}{l} p (x, y) = x^2 y^2 - 2 y^2 + xy - y + x + 1\\ q (x, y) = y + xy \end{array} \right. \]](form_339.png)
Note that the use of the Bezout matrix gives, in practice, a faster method because it is a smaller matrix than the Sylvester matrix, even if its computation takes more time (the save in the eigen-computations is greater).
We are now ready to describe our resultant-based solver. According to proposition [*] , we replace the computation of the resultant, its zeroes, and the kernel of 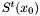 (or the Bezout matrix) for each root
(or the Bezout matrix) for each root 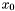 by the computation of generalized eigenvalues and eigenvectors of the associated companion matrices
by the computation of generalized eigenvalues and eigenvectors of the associated companion matrices 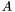 and
and 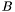 . This computation can be achieved with the QZ algorithm [GLVL96]. Here are some numerical problems which might occur: {enumeratealpha}
. This computation can be achieved with the QZ algorithm [GLVL96]. Here are some numerical problems which might occur: {enumeratealpha}
- In order to compute the
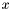 -coordinates of intersection points, it is necessary to compute the real generalized eigenvalues of
-coordinates of intersection points, it is necessary to compute the real generalized eigenvalues of 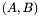 . Numerically, some of these values can contain a nonzero imaginary part. Generally such a problem is encountered for multiple eigenvalues.
. Numerically, some of these values can contain a nonzero imaginary part. Generally such a problem is encountered for multiple eigenvalues.
- What does it mean by a numerical multiple
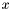 -coordinate?
-coordinate?
- How do we choose the linearly independent vectors among the computed eigenvectors? {enumeratealpha} For difficulty ``a'' we choose
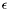 , and any eigenvalue whose imaginary part is of absolute value less than
, and any eigenvalue whose imaginary part is of absolute value less than 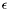 will be considered real.
will be considered real.
For difficulty ``b'', we choose possibly a different 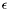 and gather the points which lay in an interval of size
and gather the points which lay in an interval of size 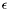 . According to the following proposition, the algorithm remains effective.
. According to the following proposition, the algorithm remains effective.
Proposition: Assume that 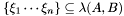 with corresponding generalized eigenvectors with corresponding generalized eigenvectors 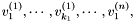 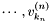 with with 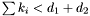 . We define . We define 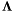 the matrix whose its rows are the matrix whose its rows are 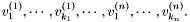 Then, if Then, if 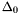 is the first left is the first left 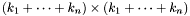 block of block of 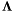 and and 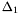 the second the second 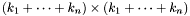 block, then the generalized eigenvalues of block, then the generalized eigenvalues of 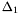 and and 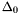 give the set of ordinates of the intersections above give the set of ordinates of the intersections above 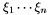 ; i.e. this algorithm can be used to gather clusters of ; i.e. this algorithm can be used to gather clusters of 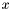 -coordinates and regarding them as the projection of only one point. -coordinates and regarding them as the projection of only one point. |
For difficulties ``c'', it is necessary to use the singular value decomposition: If 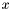 a generalized eigenvalue of
a generalized eigenvalue of 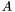 and
and 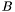 , and
, and 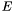 the matrix of the associated eigenvectors, then the singular value decomposition of
the matrix of the associated eigenvectors, then the singular value decomposition of 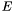 is
is
![\[ E = U \Sigma V^t, \tmop{with} \Sigma = \left( \begin{array}{cccccc} \sigma_1 & & & & & \\ & \ddots & & & & \\ & & \sigma_r & & & \\ & & & 0 & & \\ & & & & \ddots & \\ & & & & & 0 \end{array} \right) \hspace{1em} \]](form_351.png)
and 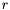 is the rank of
is the rank of 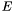 . Let
. Let
![\[ E' = E \cdot V = U \cdot \Sigma = [\sigma_1 u_1 \cdots \sigma_r u_r \hspace{0.25em} 0 \cdots 0] = [e'_1 \cdots e'_r \hspace{0.25em} 0 \cdots 0] . \]](form_352.png)
The matrix 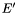 is also a matrix of eigenvectors, because the changes are done on the columns, and V is invertible. Hence
is also a matrix of eigenvectors, because the changes are done on the columns, and V is invertible. Hence 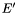 and
and 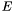 have the same rank
have the same rank 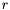 , and
, and ![$E'' = [e'_1 \cdots e'_r]$](form_354.png) is a matrix of linearly independent eigenvectors. Consequently
is a matrix of linearly independent eigenvectors. Consequently 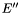 can be used to build
can be used to build 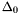 and
and 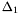 .
.
This leads to the following complete algorithm:
{Algorithm { {Numerical approximation of the root of a square bivariate system} {{-0.3cm}}
{Input:} Two bivariate polynomials ![$p (x, y), q (x, y) \in \mathbbm{R} [x, y] .$](form_356.png)
- {{Compute the Bezout matrix
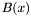 of
of 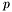 and
and 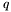 , and compute the matrices
, and compute the matrices 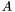 and
and 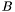 ;}}
;}}
- {{Compute the generalized eigenvalues and eigenvectors of
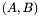 to get the
to get the 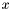 coordinates of the roots;}}
coordinates of the roots;}}
- {{Eliminate the imaginary eigenvalues and the values at infinity, and gather the close points (with the input
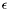 );}}
);}}
- For each of {{all the close points represented by
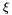 , take the matrix
, take the matrix 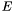 of the associated eigenvectors. If their number
of the associated eigenvectors. If their number 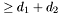 then
then 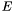 gives a basis of
gives a basis of 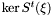 ;}}
;}}
- Compute a singular value decomposition of
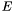 ;
;
- {{Compute the rank of
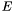 by testing the
by testing the 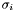 until
until 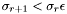 is found (the rank is thus determined to be
is found (the rank is thus determined to be 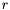 );}}
);}}
- {{Let
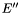 be the
be the 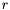 first columns of
first columns of 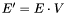 . Define
. Define 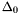 as the first
as the first 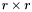 block in
block in 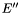 , and
, and 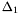 as the second
as the second 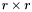 block in
block in 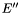 ;}}
;}}
- {{Compute the generalized eigenvalues of
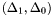 to get the
to get the 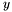 coordinates;}}
coordinates;}}
{Output:} an approximation of the real roots of 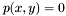 ,
, 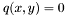 . }}{}
The function which implement this algorithm is
. }}{}
The function which implement this algorithm is
- See also:
synaps/resultant/bivariate_res.h.


#include <synaps/msolve/projection/EigenRes.h>
#ifdef SYNAPS_WITH_LAPACK
using std::cout;
using std::cin;
using std::endl;
typedef MPol<double> mpol_t;
int main(int argc, char **argv)
{
mpol_t p1("16*x0^4-160*x0^2*x1^2+400*x1^4-32*x0^3+160*x0*x1^2+6*x0^2-50*x1^2+10*x0+1.5625"),
p2("x0^2-x0*x1+x1^2-1.2*x0-0.0625");
cout<<"p1="<<p1<<endl;
cout<<"p2="<<p2<<endl;
Seq<VectDse<double> > res;
Seq<int> mux,muy;
res= solve(p1,p2, EigenRes<double>(1e-3));
res= solve(p1,p2,mux, EigenRes<double>(1e-6));
res= solve(p1,p2,mux,muy, EigenRes<double>(1e-7));
cout<<"Intersection points:"<<endl;
for(unsigned i=0;i<res.size();++i)
std::cout<<"("<<res[i][0]<<","<<res[i][1]<<") of multiplicity "<<mux[i]<<" "<<muy[i]<<std::endl;
}
#else
#include <iostream>
int main()
{
std::cout <<" LAPACK is not connected"<<std::endl;
return(77);
}
#endif //SYNAPS_WITH_LAPACK
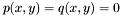 , with
, with ![$p, q \in \mathbb{R} [x, y]$](form_229.png) . It treats multiple roots, which are usually considered as obstacles for numerical linear algebra techniques. The numerical difficulties are handled with the help of singular value decomposition (SVD) of the matrix of eigenvectors associated to each eigenvalue. The extension to
. It treats multiple roots, which are usually considered as obstacles for numerical linear algebra techniques. The numerical difficulties are handled with the help of singular value decomposition (SVD) of the matrix of eigenvectors associated to each eigenvalue. The extension to 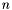 equations could be treated similarly.
equations could be treated similarly.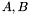 be two square matrices of size
be two square matrices of size 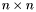 . A {generalized eigenvalue} of
. A {generalized eigenvalue} of 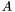 and
and 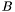 is a value in the set
is a value in the set ![\[ \lambda (A, B) : =\{\lambda \in \mathbb{C} ; \det (A - \lambda B) = 0\}. \]](form_231.png)
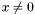 is called a {generalized eigenvector} associated to the eigenvalue
is called a {generalized eigenvector} associated to the eigenvalue 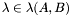 if
if 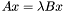 . The matrices
. The matrices 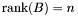 . If
. If 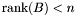 , then
, then 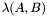 can be finite, empty, or infinite. Note that if
can be finite, empty, or infinite. Note that if 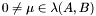 then
then 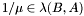 . Moreover, if
. Moreover, if 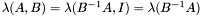 , which is the ordinary spectrum of
, which is the ordinary spectrum of 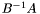 .\
.\ with polynomial coefficients can be equivalently written as a polynomial with
with polynomial coefficients can be equivalently written as a polynomial with 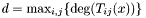 , we obtain
, we obtain 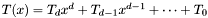 , where
, where 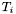 are
are ![\[ \begin{array}{c} A = \left( \begin{array}{cccc} 0 & I & \cdots & 0\\ \vdots & \ddots & \ddots & \vdots\\ 0 & \cdots & 0 & I\\ T_0^t & T_1^t & \cdots & T_{d - 1}^t \end{array} \right), \hspace{0.25em} B = \left( \begin{array}{cccc} I & 0 & \cdots & 0\\ 0 & \ddots & & \vdots\\ \vdots & & I & 0\\ 0 & \cdots & 0 & - T_d^t \end{array} \right) \end{array} . \]](form_246.png)
![\[ \hspace{1em} T^t (x) v = 0 \Leftrightarrow (A - xB) \left( \begin{array}{c} v\\ xv\\ \vdots\\ x^{d - 1} v \end{array} \right) = 0. \]](form_247.png)
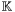 is an algebraically closed field and suppose given two bivariate polynomials
is an algebraically closed field and suppose given two bivariate polynomials  and
and 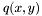 in
in ![$\mathbbm{K} [x, y]$](form_250.png) . Our aim will be to study and compute their common roots. This problem can be interpreted more geometrically. Polynomials
. Our aim will be to study and compute their common roots. This problem can be interpreted more geometrically. Polynomials 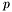 and
and 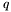 actually define two algebraic curves in the affine plane
actually define two algebraic curves in the affine plane 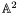 (having coordinates
(having coordinates 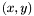 ) and we would like to know their intersection points.
) and we would like to know their intersection points.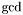 ).
).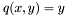 and thus we are looking for the roots of
and thus we are looking for the roots of 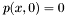 . Let us denote them by
. Let us denote them by 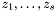 . Then we know that
. Then we know that ![\[ p (x, 0) = c (x - z_1)^{\mu_1} (x - z_2)^{\mu_2} \cdots (x - z_s)^{\mu_s}, \]](form_257.png)
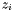 's are assumed to be distinct and
's are assumed to be distinct and 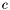 is a non-zero constant in
is a non-zero constant in 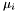 , for all
, for all 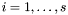 , is called the {multiplicity} of the root
, is called the {multiplicity} of the root 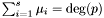 if
if 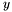 -axis (in other words, if the homogeneous part of
-axis (in other words, if the homogeneous part of 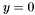 ). This later condition can be avoid in the projective setting: let
). This later condition can be avoid in the projective setting: let 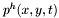 be the homogeneous polynomial obtained by homogenizing
be the homogeneous polynomial obtained by homogenizing 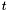 , then we have
, then we have ![\[ p (x, 0, t) = c (x - z_1 t)^{\mu_1} (x - z_2 t)^{\mu_2} \cdots (x - z_s t)^{\mu_s} t^{\mu_{\infty}}, \]](form_267.png)
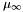 is an integer corresponding to the multiplicity of the root at infinity, and
is an integer corresponding to the multiplicity of the root at infinity, and 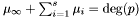 . Moreover, it turns out that the roots
. Moreover, it turns out that the roots 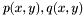 be two coprime polynomials in
be two coprime polynomials in 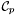 and
and 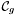 the corresponding algebraic plane curves,
the corresponding algebraic plane curves, 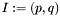 the ideal they generate in
the ideal they generate in ![$\mathcal{A} : = \mathbbm{K} [x, y] / I$](form_274.png) the associated quotient ring. We denote by
the associated quotient ring. We denote by 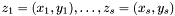 the distinct intersection points in
the distinct intersection points in 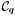 (i.e. the distinct roots of the system
(i.e. the distinct roots of the system ![\[ i (z_i, \mathcal{C}_p \cap \mathcal{C}_q) : = \dim_{\mathbbm{K}} \mathcal{A}_{z_i} < \infty, \]](form_277.png)
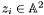 is here abusively (but usually) identified with its corresponding prime ideal in
is here abusively (but usually) identified with its corresponding prime ideal in 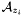 denoting the ordinary localization of the ring
denoting the ordinary localization of the ring 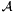 by this prime ideal. As a result, the finite
by this prime ideal. As a result, the finite ![\[ \mathcal{A} = \mathcal{A}_{z_1} \oplus \mathcal{A}_{z_2} \oplus \cdots \oplus \mathcal{A}_{z_s} \]](form_281.png)
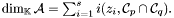
 -axis. To do this let us see both polynomials
-axis. To do this let us see both polynomials ![$A [y]$](form_283.png) where
where ![$A : = \mathbbm{K} [x]$](form_284.png) , that is to say as univariate polynomials in
, that is to say as univariate polynomials in ![\begin{equation} \label{A[x]} p (x, y) = \sum_{i = 0}^{d_1} a_i (x) y^i, \hspace{.2cm} q (x, y) = \sum_{i = 0}^{d_2} b_i (x) y^i . \end{equation}](form_285.png)
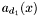 and
and 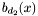 do not vanish simultaneously, as
do not vanish simultaneously, as 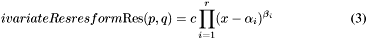
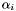 's are distinct elements in
's are distinct elements in 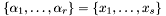 (as sets). For instance, if all the
(as sets). For instance, if all the 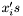 are distinct then we have
are distinct then we have 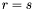 and
and 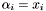 for all
for all 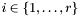 , the integer
, the integer 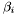 equals the sum of all the intersection multiplicity of
equals the sum of all the intersection multiplicity of 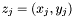 such that
such that 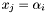 .
. 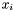 's are distinct (this can be easily obtained by a linear change of coordinates
's are distinct (this can be easily obtained by a linear change of coordinates 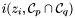 is nothing but the valuation of
is nothing but the valuation of 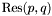 at
at 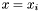 . Another corollary of this result is the well-know Bezout theorem for algebraic plane curves, which is better stated in the projective context. Let us denote by
. Another corollary of this result is the well-know Bezout theorem for algebraic plane curves, which is better stated in the projective context. Let us denote by 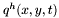 the homogeneous polynomials in
the homogeneous polynomials in ![$\mathbbm{K} [x, y, t]$](form_302.png) obtained from
obtained from 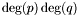 points in
points in 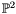 , counted with multiplicities.
, counted with multiplicities. 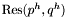 is a homogeneous polynomial in
is a homogeneous polynomial in ![$\mathbbm{K} [x, t]$](form_306.png) of degree
of degree 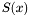 the Sylvester matrix of
the Sylvester matrix of 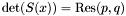 . From [*] , we deduce immediately that
. From [*] , we deduce immediately that 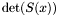 vanishes at a point
vanishes at a point 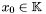 if and only if either there exists
if and only if either there exists 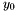 such that
such that 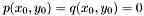 , or either
, or either 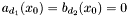 (in which case the intersection point is at infinity). Therefore one may ask the following question : being given a point
(in which case the intersection point is at infinity). Therefore one may ask the following question : being given a point 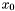 such that
such that 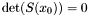 , how to recover all the possible point
, how to recover all the possible point 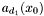 and
and 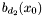 are not both zero. If
are not both zero. If 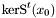 is of dimension one, then it is easy to check that there is only one point
is of dimension one, then it is easy to check that there is only one point 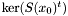 is a multiple of the vector
is a multiple of the vector ![$[1, y_0, \cdots, y_0^{d_1 + d_2 - 1}]$](form_319.png) . Therefore to compute
. Therefore to compute 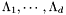 be any basis of the kernel
be any basis of the kernel 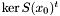 ,
, 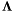 be the matrix whose
be the matrix whose 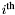 row is the vector
row is the vector 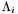 ,
, 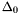 be the
be the 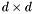 -submatrix of
-submatrix of 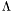 corresponding to the first
corresponding to the first 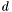 columns and
columns and 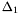 be the
be the 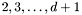 . Then
. Then 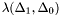 is the set of roots of the equations
is the set of roots of the equations 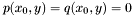 (i.e. the set of
(i.e. the set of 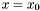 .
. 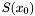 is always strictly greater than the
is always strictly greater than the 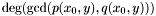 .
.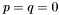 from the Sylvester matrix. However, instead of the Sylvester matrix we can use the Bezout matrix to compute
from the Sylvester matrix. However, instead of the Sylvester matrix we can use the Bezout matrix to compute ![$\tmop{Res} (p, q) \in A [x]$](form_336.png) (see section [*] ). This matrix have all the required properties to replace the Sylvester matrix in all the previous results, except in proposition
(see section [*] ). This matrix have all the required properties to replace the Sylvester matrix in all the previous results, except in proposition ![\[ \max (\deg (p (x_0, y), \deg (q (x_0, y)) > \deg (\gcd (p (x_0, y), q (x_0, y)) . \]](form_337.png)
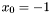 in the system
in the system ![\[ \left\{ \begin{array}{l} p (x, y) = x^2 y^2 - 2 y^2 + xy - y + x + 1\\ q (x, y) = y + xy \end{array} \right. \]](form_339.png)
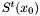 (or the Bezout matrix) for each root
(or the Bezout matrix) for each root 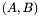 . Numerically, some of these values can contain a nonzero imaginary part. Generally such a problem is encountered for multiple eigenvalues.
. Numerically, some of these values can contain a nonzero imaginary part. Generally such a problem is encountered for multiple eigenvalues.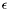 , and any eigenvalue whose imaginary part is of absolute value less than
, and any eigenvalue whose imaginary part is of absolute value less than 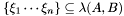 with corresponding generalized eigenvectors
with corresponding generalized eigenvectors 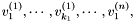
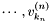 with
with 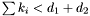 . We define
. We define 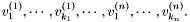 Then, if
Then, if 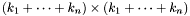 block of
block of 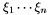 ; i.e. this algorithm can be used to gather clusters of
; i.e. this algorithm can be used to gather clusters of 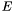 the matrix of the associated eigenvectors, then the singular value decomposition of
the matrix of the associated eigenvectors, then the singular value decomposition of ![\[ E = U \Sigma V^t, \tmop{with} \Sigma = \left( \begin{array}{cccccc} \sigma_1 & & & & & \\ & \ddots & & & & \\ & & \sigma_r & & & \\ & & & 0 & & \\ & & & & \ddots & \\ & & & & & 0 \end{array} \right) \hspace{1em} \]](form_351.png)
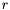 is the rank of
is the rank of ![\[ E' = E \cdot V = U \cdot \Sigma = [\sigma_1 u_1 \cdots \sigma_r u_r \hspace{0.25em} 0 \cdots 0] = [e'_1 \cdots e'_r \hspace{0.25em} 0 \cdots 0] . \]](form_352.png)
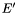 is also a matrix of eigenvectors, because the changes are done on the columns, and V is invertible. Hence
is also a matrix of eigenvectors, because the changes are done on the columns, and V is invertible. Hence ![$E'' = [e'_1 \cdots e'_r]$](form_354.png) is a matrix of linearly independent eigenvectors. Consequently
is a matrix of linearly independent eigenvectors. Consequently 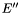 can be used to build
can be used to build ![$p (x, y), q (x, y) \in \mathbbm{R} [x, y] .$](form_356.png)
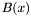 of
of 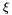 , take the matrix
, take the matrix 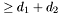 then
then 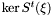 ;}}
;}}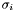 until
until 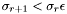 is found (the rank is thus determined to be
is found (the rank is thus determined to be 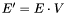 . Define
. Define 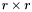 block in
block in 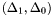 to get the
to get the 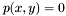 ,
, 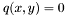 . }}{}
. }}{}