
Pascal Cachier and David Rey
INRIA Sophia - Epidaure Project
2004 Route des Lucioles BP 93
06902 Sophia Antipolis Cedex, France
{Pascal.Cachier, David.Rey}@sophia.inria.fr

Non-rigid registration of two images I and J consists in finding a transformation between the two sets of points of both images. If we make the assumption that every point of an image has an homologous point in the other, and that the topology has been conserved, the result of the algorithm should be a smooth homeomorphic transformation T(I, J), going from I to J.
Among non-rigid registration algorithms, intensity-based algorithms
are driven by a similarity energy Esim (e.g. the sum of square
differences (SSD)) that attracts both images toward each other using
their intensity values [1]. At the same time, the
transformation T(I,J) is kept smooth either by constraining T(I,J)to belong to some space
![]() of regular transformations (e.g.
splines with few control points [2]), or by choosing a
regularization energy Ereg (e.g. the linear elastic energy), or
both [3]. This energy Ereg can be minimized with
Esim in a weighted sum
of regular transformations (e.g.
splines with few control points [2]), or by choosing a
regularization energy Ereg (e.g. the linear elastic energy), or
both [3]. This energy Ereg can be minimized with
Esim in a weighted sum
![]() [4,5], or minimized alternatively with
Esim [6]. See [7] for a review of
registration techniques.
[4,5], or minimized alternatively with
Esim [6]. See [7] for a review of
registration techniques.
Without any other prior knowledge, the registration problem is symmetric and we expect to obtain the inverse transformation if we exchange I and J: T(J, I) = [T(I, J)]-1. However, this symmetry is usually broken in practice, giving birth to the terminology ``reference'' or ``template'' image and ``study'' or ``floating'' image (here T(I, J) goes from the reference image Ito the study image J). Most, if not all, of the energies used in medical image non-rigid registration leads to asymmetrical registration. This includes the usual similarity energies and quadratic regularization energies such as linear elastic or thin plate energies. Even the general, non-linear elasticity is conceptually asymmetric since one of the images is supposed to be in a no-stress state and not the other; see [8] for an example showing the importance of this consideration.
The first obvious problem with asymmetry is that we have to choose arbitrarily a reference image, and thus the results of measures relying on this registration depend on how the reference image is chosen.
However, there can be a more subtle problem than the previous one. Indeed, using standard similarity measures and quadratic regularization energies will lead to systematically biased solutions: they will smooth the transformation on expanding regions more than on shrinking regions. Both T(I, J) and T(J, I) will have more difficulty to describe a local growth than a local shrink.
6.2cm
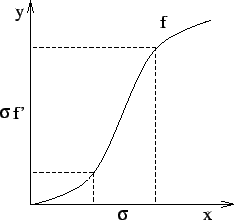
|
![[*]](cross_ref_motif.gif) , the same
smoothing is approximately obtained on f-1 if it is convolved
with a kernel of size
, the same
smoothing is approximately obtained on f-1 if it is convolved
with a kernel of size This explains why the detection of evolving brain lesions using non-rigid registration has appeared easier on shrinking lesions than on expanding lesions in our previous work [9]. We thus detected expanding and shrinking regions by working on shrinking regions of both T(I, J) and T(J, I).
We have found that the asymmetry of intensity-based non-rigid registration is due to one or several of the following reasons:
1. Order non-preservation of the energies: An energy E (I, J, T) being used for registration, we may have E(I, J, T1) < E(I, J, T2) but not E(J, I, T1-1) < E( J,I, T2-1) for two estimates T1 and T2 of the transformation.
2. Non-stable transformation space: The space of allowed
transformation
![]() may not be a group and thus not stable
by inversion, i.e. we may have
may not be a group and thus not stable
by inversion, i.e. we may have
![]() but not
but not
![]() .
.
3. Local Minima: The optimization algorithm may get stuck in different local minima of the energy when the images are exchanged.
A previous work on the symmetrization of the registration has been done by Christensen [5]. In his work, two asymmetric registrations are made simultaneously, but are constrained to be close to the inverse of each other. This constraint is efficient at smoothing the registration. However, the algorithm is only asymptotically symmetric when the weight of this constraint tends towards infinity. Also, it relies on the computation of an inverse transformation whose existence is not ensured by linear elasticity. This work is nice but we felt that the symmetrization could be handled theoretically in a more efficient way.
In this paper, we propose to tackle the first point of the previous
list and to ensure that the minima of the energy are invariant when
exchanging the images, by forcing the similarity energy Esim and
the smoothness energy Ereg to be symmetric, i.e. invariant if we
exchange I and J and invert the transformation:
![]() .
This is close to a very recent work by Trouvé and
Younes [10] where the authors consider distances of two
parametric closed curves verifying some properties, including this
kind of symmetry.
.
This is close to a very recent work by Trouvé and
Younes [10] where the authors consider distances of two
parametric closed curves verifying some properties, including this
kind of symmetry.
In section ![[*]](cross_ref_motif.gif) we present a way to construct symmetric
energies. In section
we present a way to construct symmetric
energies. In section ![[*]](cross_ref_motif.gif) we present two
optimization procedures, depending on whether we compute the inverse
transformation or not. We illustrate the theory with a synthetic
example in section
we present two
optimization procedures, depending on whether we compute the inverse
transformation or not. We illustrate the theory with a synthetic
example in section ![[*]](cross_ref_motif.gif) , and in section
, and in section
![[*]](cross_ref_motif.gif) we show the interest of this method to detect
and segment evolving lesions in multiple sclerosis.
we show the interest of this method to detect
and segment evolving lesions in multiple sclerosis.
Let
![]() be a point of I, and let
be a point of I, and let
![]() be the n-th
differential tensor of T at
be the n-th
differential tensor of T at
![]() .
Let
Ereg(T) be a regularization
energy that can be written as an integral of some function e2 of
the differentials of T:
.
Let
Ereg(T) be a regularization
energy that can be written as an integral of some function e2 of
the differentials of T:
Ereg is symmetric (or inversion invariant) if
Ereg(T) =
Ereg(T-1). If we change variables in
Ereg(T-1)
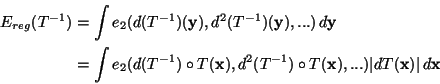
it appears that a sufficient condition for Ereg to be symmetric is
that
There are many such symmetric energies. Among them, we are more
particularly interested in energies that are somehow linked to the
asymmetric energies we are used to. There are several possibilities to
symmetrize an asymmetric energy. Among them, the most natural is
perhaps to take the mean of
e2(dT, d2T, ...) and
![]() ,
i.e. the
symmetrization Ereg* of a regularization energy Ereg can be
defined by
,
i.e. the
symmetrization Ereg* of a regularization energy Ereg can be
defined by
The trick is that
![]() can
be calculate (more or less easily) from the derivatives of T. Thus,
E*reg(T) is indeed of the form (
can
be calculate (more or less easily) from the derivatives of T. Thus,
E*reg(T) is indeed of the form (![[*]](cross_ref_motif.gif) ) and can be computed
without inverting T. For example, let us consider the following
quadratic energy in 2D:
) and can be computed
without inverting T. For example, let us consider the following
quadratic energy in 2D:
![]() .
Since
.
Since
![]() ,
we find that the symmetrization of
this energy using eq. (
,
we find that the symmetrization of
this energy using eq. (![[*]](cross_ref_motif.gif) ) is:
) is:
Note that the integrand tends to ![]() when dT tends to 0: in
practice, this will force the transformation to be one-to-one.
when dT tends to 0: in
practice, this will force the transformation to be one-to-one.
Similarity measures can be symmetrized using the same technique. If
Esim(I, J, T) is a similarity energy, a symmetric
similarity energy can be deduced by setting:
Here again, changing the variables inside
Esim(J, I, T-1)usually eliminates T-1 from the formulas, and therefore the
inversion of T can be avoided. For example, if
![]() is the standard SSD criterion between two
images, then its symmetrization using (
is the standard SSD criterion between two
images, then its symmetrization using (![[*]](cross_ref_motif.gif) ) is
) is
Our first implementation uses the fact that the symmetric energies can
be computed and optimized without inverting the displacement field. To
produce the results presented in the next section, we have minimized
in 2D
the symmetric energy (![[*]](cross_ref_motif.gif) ) which is the symmetrization of (
) which is the symmetrization of (![[*]](cross_ref_motif.gif) ):
):
In our experiences, the accuracy of the symmetry has been very sensitive to the discretization of the continuous optimization problem. We found out that results were significantly better using a finite element discretization of the energy rather than a finite difference scheme. A triangularization of the rectangular grid defined by the pixels is used. The images as well as the transformation are defined as piecewise linear functions on this triangularization. To minimize the energy, we use a simple gradient descent coupled with a multiresolution scheme.
We encountered two types of problems with the previous algorithm:
![[*]](cross_ref_motif.gif) ) with respect to T uses the derivative of
J and not the derivative of I. This hampers a perfect symmetry
of the result.
) with respect to T uses the derivative of
J and not the derivative of I. This hampers a perfect symmetry
of the result.
These last problems can be avoided if we compute the inverse
transformation. Our second method uses a very simple yet efficient
alternated-minimization method: instead of minimizing
E*(I, J, T) =
E(I, J, T) + E(J, I, T-1), we minimize alternatively the
asymmetric energies
E(I, J, T) and
E(J, I, T-1) (given by eq.
(![[*]](cross_ref_motif.gif) )) using respectively I and J as the reference
image. This requires an inversion of the transformation every time we
change of reference image.
)) using respectively I and J as the reference
image. This requires an inversion of the transformation every time we
change of reference image.
For a better comparison with the previous algorithm in 2D we have used the same finite element discretization. However, it is not necessary, which is one advantage of this method: faster optimizations are possible with the same quality of symmetry.
The inverse transformation is computed by finding the zero of
![]() using a Newton scheme.
Interpolation of the transformation is necessary; we have used a bi-
or trilinear interpolation. The inverse is found with an error
usually less than 0.1 voxel. Note that we cannot have an
arbitrarily small error because the inverse of a piecewise
bi/trilinear transformation is not piecewise bi/trilinear.
using a Newton scheme.
Interpolation of the transformation is necessary; we have used a bi-
or trilinear interpolation. The inverse is found with an error
usually less than 0.1 voxel. Note that we cannot have an
arbitrarily small error because the inverse of a piecewise
bi/trilinear transformation is not piecewise bi/trilinear.
We have to be careful with the computation of the inverse. Indeed, E(I, J, T) does not guarantee that the transformations is invertible. Forcing the corrections brought at each iteration to be small, and/or smoothing them, often helps the transformation to be invertible at every iteration, especially during the first iterations at full resolution when only a small number of points are moving. Furthermore, imposing small corrections seems to give more symmetrical results.
In this synthetic example we have two
![]() images
containing two discs, one multiplying its radius by 2 and the other
shrinking symmetrically (fig.
images
containing two discs, one multiplying its radius by 2 and the other
shrinking symmetrically (fig. ![[*]](cross_ref_motif.gif) ). We have registered these
images using the asymmetric energy (
). We have registered these
images using the asymmetric energy (![[*]](cross_ref_motif.gif) ) (Asym
algorithm), and using the algorithms described in sec.
) (Asym
algorithm), and using the algorithms described in sec. ![[*]](cross_ref_motif.gif) (Sym1) and sec.
(Sym1) and sec. ![[*]](cross_ref_motif.gif) (Sym2).
(Sym2).
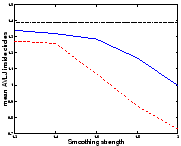
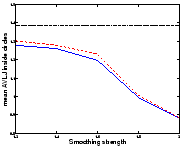
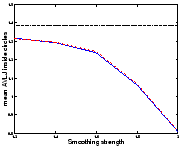
![[*]](cross_ref_motif.gif) that shrinkage is more
easily recovered than growth. We can analyse it using the absolute
value of the logarithm of the Jacobian (AVLJ) of the transformation,
which expresses the local increase or decrease of area and we used for
the detection of brain evolution in [9]. If the growth and
the shrinkage were recovered equally, we would find equal AVLJ inside
both circles, and if they were furthermore exactly recovered, these
numbers would be equal to
that shrinkage is more
easily recovered than growth. We can analyse it using the absolute
value of the logarithm of the Jacobian (AVLJ) of the transformation,
which expresses the local increase or decrease of area and we used for
the detection of brain evolution in [9]. If the growth and
the shrinkage were recovered equally, we would find equal AVLJ inside
both circles, and if they were furthermore exactly recovered, these
numbers would be equal to
![[*]](cross_ref_motif.gif) ). This shortcoming is reduced with
Sym1, and virtually eliminated with Sym2. We have
also registered the images in both directions and computed
). This shortcoming is reduced with
Sym1, and virtually eliminated with Sym2. We have
also registered the images in both directions and computed
![[*]](cross_ref_motif.gif) ) and confirm the
previous results.
) and confirm the
previous results.
We would like to emphasize that for the same amount of smoothing, Sym1 and Sym2 do not find a solution closer to the real transformation than the asymmetric algorithm for both circles: the small circle is registered better but the big circle is less shrinked. The distance to the real transformation is not uniformally decreased; errors are just shared more equitably.


 |
In this section we would like to show that the method described in this paper can significantly improve results in the detection and segmentation of evolving lesions in multiple sclerosis [11,9]. In a previous article [9] we explain that small expanding lesions can be difficult to detect with temporal analysis of apparent deformations: if there is an important expansion locally between images I and J, we would need a one to many mapping due to limited resolution of the image. To avoid this, we considered only shrinking regions from I to J, and then shrinking regions from J to I. By thresholding shrinking areas we obtained the sought segmentations.
However it is possible to avoid the computation of 2 vector fields
(direct and reverse) between images I and J, by computing only one
vector field thanks to a symmetrical approach. Here, we have used the
alternated minimization method (sec. ![[*]](cross_ref_motif.gif) ), without using a
finite element scheme but the fast scheme of [6].
), without using a
finite element scheme but the fast scheme of [6].
We have made some experiments on an evolving lesion extracted from two
T2-weighted MRI of a patient with multiple sclerosis. Time between the
two acquisitions is 8 weeks. The resolution of the images is really
poor as we can see on the first two columns of figure ![[*]](cross_ref_motif.gif) (voxel size is
(voxel size is
![]() mm3). We have computed four
vector fields for our experiment: asymmetric and symmetric fields from
I to J, and asymmetric and symmetric fields from 2 to 1. We
compute the Jacobian on each field, and we manually search for the
Jacobian isovalue (in red on fig.
mm3). We have computed four
vector fields for our experiment: asymmetric and symmetric fields from
I to J, and asymmetric and symmetric fields from 2 to 1. We
compute the Jacobian on each field, and we manually search for the
Jacobian isovalue (in red on fig. ![[*]](cross_ref_motif.gif) ) that segments the
lesion. As explained in [9], it does not exist any efficient
automatic method to find the best threshold at the moment.
) that segments the
lesion. As explained in [9], it does not exist any efficient
automatic method to find the best threshold at the moment.
 |
![[*]](cross_ref_motif.gif) manual
segmentations were done independently. Values are not inverse in the
case of asymmetrical computation, and inverse in the case of
symmetrical approach. Furthermore, the segmentation of evolving areas
seems to better correspond to reality as we can see in figure
manual
segmentations were done independently. Values are not inverse in the
case of asymmetrical computation, and inverse in the case of
symmetrical approach. Furthermore, the segmentation of evolving areas
seems to better correspond to reality as we can see in figure
![[*]](cross_ref_motif.gif) .
.
In this paper we have listed the reasons of the asymmetry of intensity-based registration algorithms. We have shown that asymmetry may hamper the equal retrieval of expanding and shrinking areas, perturbing registration-based detection of evolving processes. To reduce the asymmetry of registration, we have introduced inversion-invariant similarity and smoothness energies, and a way to symmetrize the widely used asymmetric energies.
We have worked on a particular asymmetric energy E* that is easily expressed as a function of the transform T. We have minimized E*with and without computation of the inverse transform. On a synthetic example, we have shown that the use of a symmetric energy was reducing considerably the shortcomings of asymmetric energies, and that the computation of the inverse transform, if it exists, is helpful. Finally, a symmetric approach improves segmentation results and simplify the methodology of registration-based detection of evolving lesions, especially in the case of small lesions and/or poor resolution.
http://www.inria.fr/RRRT/RR-3706.html.
http://www.inria.fr/RRRT/RR-3559.html.
For a better comprehension, we develop the mathematics for obtaining
the symmetric energies (![[*]](cross_ref_motif.gif) ) and (
) and (![[*]](cross_ref_motif.gif) ). If
). If
![]() is a diffeomorphic 2D transformation, we can
compute its Jacobian matrix at a point
is a diffeomorphic 2D transformation, we can
compute its Jacobian matrix at a point
![]()
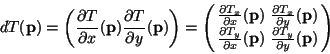
![[*]](cross_ref_motif.gif) ),
),
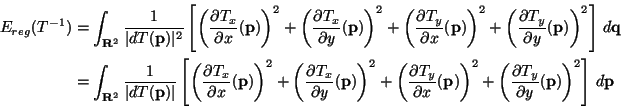
![[*]](cross_ref_motif.gif) )).
)).
Similarly, if
![]() ,
,
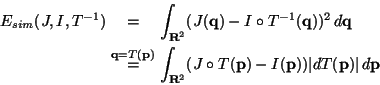
![[*]](cross_ref_motif.gif) ) by summing this last equation to
Esim(T).
) by summing this last equation to
Esim(T).