Back to the main documentation of CtCoq

In this page, we present a tool that uses the mouse to quicken some frequent operations on mathematical formulas. This tool uses a paradigm of object dragging to replace expressions by provably equivalent formulas, using the Coq command Rewrite. We give an overview of its use, with a short example, and we show how this mechanism can be adapted to the mathematical domain of your choice. This parametrisation uses behavior rules, we will show how these rules can be obtained from certain classes of theorems and how these rules can also be edited manually.

Introduction: Making some rewriting operations easy.

To perform rewriting in CtCoq, users must normally construct a Rewrite command where they must provide a theorem, the parameters for its instantiation, and the position where the rewriting occurs. In the tool we present here, these three kinds of parameters are determined simply when the user "drags" an expression with the mouse, by clicking on it, moving the mouse, and releasing the button (with the <Ctrl> key depressed and the left button of the mouse). The drag movement can convey some intuitive information, when the replacement has the effect of moving one piece of data from one place to the other.

In general, the drag movement is used to express one of several kinds of operations:

1. The combination of two expressions on the screen, like the two x's in the expression "x - x" (and replace it by "0", this will be expressed by taking one of the x's and dragging to the other one) or the + and the * in the expression "x * ( y + z)" (and replace it by "x * y + x * z", this will be expressed by taking the + and dragging it to the *).
2. The movement of some expression with respect to other expressions, like when one wants to replace "x + y" by "y + x" or "x + (y + z)" by "y + (x + z"). In both cases this will be expressed by taking the x and moving it to the y.
3. The cancellative effects of several operations together, "-(-x)" which can be replaced by "x". This will be expressed by taking one of the "-" signs and moving it to the other.
4. The permutation of operators like in "-(1/x)" which can be replaced by "1/(-x)". This will be expressed by taking the "-" sign and moving it on the "1/" sign.
5. The rearrangement of complex structures like associative patterns of the form "(x + y) + z", which can be replaced by "x + (y + z)". This will be expressed by taking the parentheses and and moving them to the second "plus" sign, to express that we want the parentheses around the second sum.

An animated example

In this example, an arrow appears when the user is depressing the left button of the mouse while also depressing the <Ctrl> key of the keyboard. The pink and green colors appear in the normal behavior of the tool. They give some visual feedback to the user.

This animation shows four actions provoked by the user. The first one permutes two instances of x and y, the second one cancels the expression z - z, the third one cancels a neutral element, and the fourth one permutes two other expressions. Each of these actions would actually produce a command to insert in the Command window and, when the Auto do-it flag is on, this command would be directly executed, giving a result very close in speed to this animation.

The default behavior

We give here the list of all the theorems that can be triggered by the default behavior of our drag-and-drop mechanism.

Combination theorems

Permutation theorems

Extending the drag-and-drop algorithm

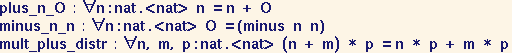
We have devised a language of drag-and-drop behavior rules, where each possible reaction performed by the drag-and-drop tool is described by a separate behavior rule. To ensure the validity of each operation, each rule rests on a rewriting theorem whose proof should be done separately. Behavior rules can be edited manually, using an interactive editor. We also provide automatic tools that directly infer simple behavior patterns from the form of rewriting theorem statements, when these theorems belong to well known classes of theorems.