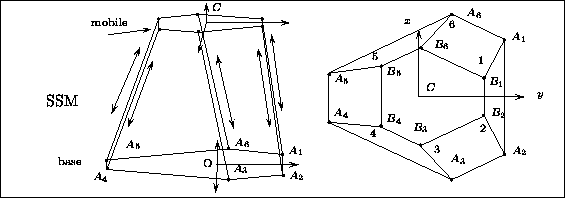
Figure 1: The geometry of the robot
FK-ssm enables to compute all the solutions of the forward kinematics of a Gough platform parallel robot, with special constraints on the positions of the joint's centers.
Free source codes are available under Free Software Society conventions through anonymous ftp (download here).
This software is provided "as is" without warranty of any kind. In no event shall INRIA be liable for any loss of profits, loss of business, loss of use or data, interruption of business, or for indirect, special, incidental, or consequential damages of any kind, arising from any error in this software.
Window system: none
Type: sources
Language: C
Number of lines: 3000
Size of binary: 1.73 Mo
Output: solutions of the forward kinematics
History:
version 0.1:8/6/1995
version 0.2:10/10/1996 patched on 25/3/1997
FK-ssm enables to compute all the solutions of the forward kinematics of a Gough platform parallel robot, with special constraints on the positions of the joint's centers.
The general geometry of the robot is presented in figure 1.

Figure 1: The geometry of the robot
The forward kinematics problem is to find the position/orientation of the moving platform for a given set of leg lengths.
If xai,yai,zai denote the coordinates of the centers of the joints on the base they should fulfill the following constraints:
The geometry of such a robot is defined in a file in which the 12x3 coordinates of the centers are given, first for the base, then for the platform. For example a valid file is:
-9.758000 9.098000 0.0 9.758000 9.098000 0.0 12.758000 3.902000 0.0 3.000000 -13.000000 0.0 -3.000000 -13.000000 0.0 -12.758000 3.902000 0.0 -3.000000 7.300000 0.0 3.000000 7.300000 0.0 7.821800 -1.052000 0.0 4.821800 -6.248000 0.0 -4.821800 -6.248000 0.0 -7.821800 -1.052000 0.0in which the 6 first lines define the coordinates of the base joints, and the 6 last lines the coordinates of the platform joint.
This program is an implementation of the algorithm described in [2],[1]. To run the program use the command:
FK-ssm [mechanism file]The program will then ask you:
Acknowledgment: I am indebted to Imme Ebert-Uphoff which has found a bug in this program, leading to the implementation of version 0.2