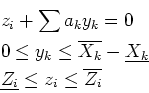
 Next: 20 Opérateurs d'unicité
Up: 19 Les opérateurs rétractant
Previous: 19.5 Newton intervalle multivariable
Soit un système
Next: 20 Opérateurs d'unicité
Up: 19 Les opérateurs rétractant
Previous: 19.5 Newton intervalle multivariable
Soit un système
![$f_i(x_1,x_2,\ldots,x_n)=0, i \in [1,m]$](img92.png) et
et
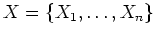
Posons
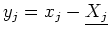 et supposons que les
et supposons que les 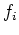 contiennent
au moins un terme linéaire dans un des
contiennent
au moins un terme linéaire dans un des 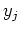 . On a
. On a
où les 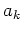 sont des constantes et les
sont des constantes et les 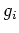 représente la partie
non-linéaire de
représente la partie
non-linéaire de 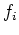 . Posons
. Posons 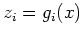 et
et 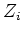 l'évaluation
par intervalle de
l'évaluation
par intervalle de 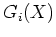 . On a alors:
. On a alors:
un système linéaire d'égalités et d'inégalités dans les
variables 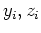
On peut alors utiliser la méthode du simplex pour:
- déterminer s'il existe une région faisable pour ce système
(sinon pas de solution)
- déterminer le minimum
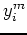 et le maximum
et le maximum 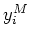 des
des 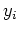 :
:
- si
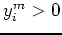 , alors
, alors
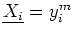
- si
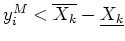 , alors
, alors
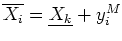
- la mise à jour d'une variable implique de recalculer
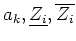

 Next: 20 Opérateurs d'unicité
Up: 19 Les opérateurs rétractant
Previous: 19.5 Newton intervalle multivariable
Jean-Pierre Merlet
Next: 20 Opérateurs d'unicité
Up: 19 Les opérateurs rétractant
Previous: 19.5 Newton intervalle multivariable
Jean-Pierre Merlet
2007-05-18
![]() et supposons que les
et supposons que les ![]() contiennent
au moins un terme linéaire dans un des
contiennent
au moins un terme linéaire dans un des ![]() . On a
. On a