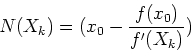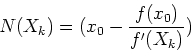
 Next: 19.5 Newton intervalle multivariable
Up: 19 Les opérateurs rétractant
Previous: 19.3 Consistance: méthode B
Soit
Next: 19.5 Newton intervalle multivariable
Up: 19 Les opérateurs rétractant
Previous: 19.3 Consistance: méthode B
Soit
où 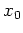 appartient à l'intervalle
appartient à l'intervalle 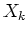 (par exemple
(par exemple
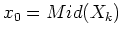 )
)
alors:
-
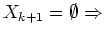 pas de solution de
pas de solution de 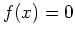 dans
dans
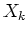
- s'il existe un zéro de
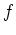 dans
dans 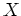 alors il appartient
aussi à
alors il appartient
aussi à 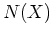
- si
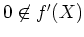 alors il existe
alors il existe 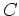 tel que
tel que
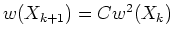
- si
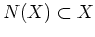 alors il existe un zéro de
alors il existe un zéro de 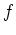 dans
dans
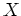
- si
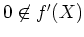 et il existe un zéro de
et il existe un zéro de 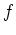 dans
dans
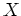 , alors ce zéro est unique dans
, alors ce zéro est unique dans 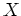

 Next: 19.5 Newton intervalle multivariable
Up: 19 Les opérateurs rétractant
Previous: 19.3 Consistance: méthode B
Jean-Pierre Merlet
Next: 19.5 Newton intervalle multivariable
Up: 19 Les opérateurs rétractant
Previous: 19.3 Consistance: méthode B
Jean-Pierre Merlet
2007-05-18