



Next: Function involving determinants
Up: Equations, Gradient and Hessian
Previous: MakeF, MakeJ, MakeH
Contents
Improving the efficiency of the code
It may happen that the evaluation of an expression involves many time the
evaluation of a sub-expression. Clearly evaluating only once these
sub-expressions will speed up the code.
This may be done through a user-provided Maple procedure that must
be called ALIAS_FSIMPLIFY. This procedure takes as input a
file descriptor
and an expression expr. It will be first called right after the creation
of the evaluation file with a string: detecting that expr is a string
allow to write some initialization. Then it will be called before writing
any equation to allow for simplification.
For example assume that an expression that will be treated by the
Make[FJH] procedure involves numerous time the evaluation of the
sine and cosine of the first variable x (whose name in ALIAS-C++ is
v_IS(1)).The ALIAS_FSIMPLIFY procedure may be written as:
ALIAS_FSIMPLIFY:=proc(fid,expr)
local aux:
if type(expr,string) then
fprintf(fid,"INTERVAL SS,CC;\n"):
fprintf(fid,"SS=Sin(v_IS(1));\n"):
fprintf(fid,"CC=Cos(v_IS(1));\n"):
RETURN(0):
fi:
aux:=expr:
aux:=subs(sin(x)=SS,cos(x)=CC,aux):
RETURN(aux):
end:
This procedure will be first called with a string for expr and a
consequence is that at the beginning of the evaluation file fid
the interval variable SS,CC will be defined and then assigned to
the value of
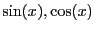 . Then the procedure will be called for
each expression that will be assigned to expr: each occurrence of
the sine and cosine of
. Then the procedure will be called for
each expression that will be assigned to expr: each occurrence of
the sine and cosine of 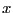 in the expression will be substituted by
SS, CC.
in the expression will be substituted by
SS, CC.
The procedure Math_Func, see section 9.4, may be
used to identify mathematical functions occurring in an expression and
the list provided by this function may be used to write a generic
ALIAS_FSIMPLIFY procedure that will automatically compute only
once the more complex components of an expression. The procedure Auto_Diff, see section 2.3.2, may also be used to speed up
the interval evaluation of an expression. Note also that a similar
mechanism exists for expression involving determinants of matrices.




Next: Function involving determinants
Up: Equations, Gradient and Hessian
Previous: MakeF, MakeJ, MakeH
Contents
Jean-Pierre Merlet
2012-12-20