Function involving determinants

A determinant of a matrix A may appear in an equation using one of the syntax:

 
Fast_Determinant(A)  Medium_Determinant(A)  Slow_Determinant(A)

the differences between the syntax being only in the computation time (from the fastest to the slowest) and in the width of the interval evaluation (from the largest to the narrowest). If you are interested in determining if a determinant may cancel you may also use Slow_NonZero_Determinant which is faster than Slow_Determinant.

Note that if determinants are present in the equations there are different ways to compute the determinant:

1. by using Gaussian elimination. This method will be used only if the flag `ALIAS/use_gaussian_elim_det` is set to 1
2. either by computing only the intervals for each component of the matrix and using a row or column expansion to determine the interval evaluation of the determinant
3. same as above but the gradient of the coefficients are used to improve their interval evaluation
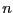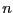4. by computing symbolically every minors of dimension $n$ of the matrix and using the interval evaluation of these expressions to compute the interval evaluation of the determinant. The value of $n$ is given by `ALIAS/minor22 (default value: 2)
5. a mix of method 2 and 3

or pre-computing an interval expression for all the dimension 2 minors (thereby using, for example, either the Fast_Determinant or the Fast_Determinant22 procedures. The second procedure will, in general, lead to better interval evaluation but Maple may take some time to produce the corresponding source code. You may choose one of these ways by setting the flag `ALIAS/det22` to 0, 1, 2 or 3 (default value: 0). Clearly the values 2 and 3 should be avoided for large matrix as the Maple computation time and the size of the generated code may be large. If the determinant of minors is used, then the expansion will be done according either to the row or to the column according to the value of `ALIAS/row22`. A value of 0 (the default value means that the expansion will done along the rows and for any other value according to the column).

Note that you may speed up the interval evaluation of functions including determinant of matrices (which are often computer intensive) by defining intermediate interval variables and substituting these variables in the expression. For example assume that the coefficients of a matrix A involve a large number of sine and cosine depending upon the unknown 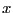$x$, the first unknown in our list of unknowns: you first define a Maple procedure intro_A that return an array of strings that contain all the definition of the intermediate variables. In our case the procedure is:

 
intro_A=proc()
local h;
h:=["INTERVAL SX;SX=Sin(v_IS(1));","INTERVAL SY;SY=Cos(v_IS(1));"]
RETURN(h);
end:

Note that the name of the unknowns in the code generated by ALIAS is v_IS. The two strings of the array h will be automatically inserted in the C++ procedure generated by ALIAS. Hence the intermediate variable SX, SY will contain the value of the interval evaluation of 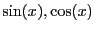$\sin(x), \cos(x)$. You may then write the simplification procedure that will substitute every occurrence of Sin(v_IS(1)) and Cos(v_IS(1)) by SX and CX. The name of this procedure must be simplify_A and is written as:

 
simplify_A:=proc(eq)
local eq1;
eq1:=subs(Sin(v_IS(1))=SX,Cos(v_IS(1)=CX,eq):
RETURN(eq1);
end: