



Next: Roots simplification procedures
Up: Filtering simplification procedures
Previous: The SimplexConsistency procedure
Contents
This procedure allows one to take into account the specific structure
of the system to solve when using the interval Newton method. In this
method the classical algorithm, for example used by default in GradientSolve or HessianSolve, computes numerically for a box 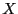 the interval evaluation
of
the interval evaluation
of
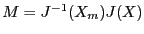 where
where 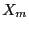 is the mid-point of
is the mid-point of 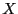 . This
numerical calculation does not allow to to take into account the
dependency between the elements of
. This
numerical calculation does not allow to to take into account the
dependency between the elements of 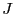 when computing
when computing 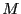 . This
procedure compute symbolically the matrix
. This
procedure compute symbolically the matrix 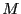 and re-arrange its
elements (with MinimalCout) in order to reduce the dependency
problem.
and re-arrange its
elements (with MinimalCout) in order to reduce the dependency
problem.
The syntax of this procedure is
IntervalNewton(func,nfunc,funcproc,njfunc,Jfuncproc,typemid,grad,grad3B,incl,vars,procname)
where
- func: the list of equations,
- nfunc: the number of equations that will be evaluated by
funcproc. It may not be the same than the number of equations in
func
- funcproc: the name of the procedure that is used to evaluate
the equations. It may be the name of a procedure designed by the
end-user with MakeF or the name of the procedure that will be
used by the solving algorithm (usually "F")
- njfunc: the number of equations that will be used when
computing the derivatives. It may not be the same than the number of equations in
func
- Jfuncproc: the name of the procedure that is used to evaluate
the derivative of the equations. It may be the name of a procedure designed by the
end-user with MakeJ or the name of the procedure that will be
used by the solving algorithm (usually "J")
- typemid: the interval Newton method uses a conditioning
matrix. This flag will indicate which type of conditioning matrix is
used. If 0 we use
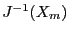 , if 1
, if 1
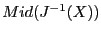 ,
if 2 both above conditioning matrices will be used
,
if 2 both above conditioning matrices will be used
- grad, grad3B: it is possible to use the derivatives of
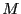 to improve the interval evaluation. If grad is set to 1 this
will be used for all boxes in the algorithm. If grad3B is set to
1 it will also be used for the sub-boxes that are considered when
using the 3B method
to improve the interval evaluation. If grad is set to 1 this
will be used for all boxes in the algorithm. If grad3B is set to
1 it will also be used for the sub-boxes that are considered when
using the 3B method
- incl: a list. If the end-user uses a specific procedure to
compute the interval evaluation of func, then incl[1]
should be set to 1. Similarly if it uses its own procedure to compute
the derivatives of func, then incl[2] should be set to 1.
- vars: the list of variables. All
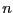 unknowns in the
unknowns in the 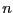 elements of func
must appear first in this list
elements of func
must appear first in this list
- ProcName: the name of the simplification procedure that
will be created in the file ProcName.C




Next: Roots simplification procedures
Up: Filtering simplification procedures
Previous: The SimplexConsistency procedure
Contents
Jean-Pierre Merlet
2012-12-20
![]() the interval evaluation
of
the interval evaluation
of
![]() where
where ![]() is the mid-point of
is the mid-point of ![]() . This
numerical calculation does not allow to to take into account the
dependency between the elements of
. This
numerical calculation does not allow to to take into account the
dependency between the elements of ![]() when computing
when computing ![]() . This
procedure compute symbolically the matrix
. This
procedure compute symbolically the matrix ![]() and re-arrange its
elements (with MinimalCout) in order to reduce the dependency
problem.
and re-arrange its
elements (with MinimalCout) in order to reduce the dependency
problem.