



Next: Non 0-dimensional system
Up: Linear algebra
Previous: The LinearMatrixConsistency procedure
Contents
Any ALIAS maple procedure involved in the calculation on eigenvalues
of a matrix A may use the Gerschgorin circles methods that states that
all the eigenvalues of a matrix are enclosed in the union of a set of
circles (in the complex plane) whose center and radii are calculated as
functions of the coefficients of the matrix.
The purpose of the GerschgorinConsistency procedure is to
generate the C++ code for a simplification
procedure that may be used by the ALIAS-Maple procedures doing
calculation on the eigenvalues of a square matrix.
The syntax is:
GerschgorinConsistency(Func,Vars,Gradient,n,procname)
where:
- Func: list of constraints (equation or inequality), the
last element must be the matrix.
- Vars: list of parameters name including as first element
an auxiliary name that will be the name of the unknown in the
characteristic polynomial name
- Gradient: a flag that indicates if the derivatives of the
matrix coefficients with respect to the unknowns may be used (1) or not (0)
- n: an integer, the order of the method, see below
- procname: the name of the simplification procedure. The
name of the created file will be procname.C
Here we try to improve the bounds given by the Gerschgorin method using
the fact that for any diagonal matrix D with positive components the
eigenvalues of 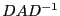 are the same than the eigenvalues of A. The method
is not able to determine D such that the Gerschgorin circles are minimal
(i.e. give the best bounds) and only try a set of at most
are the same than the eigenvalues of A. The method
is not able to determine D such that the Gerschgorin circles are minimal
(i.e. give the best bounds) and only try a set of at most 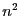 different D
where n is the order of the method.
different D
where n is the order of the method.
To check only if the eigenvalues lie in the interval provided by the C++
procedure without modifying this interval use a negative n




Next: Non 0-dimensional system
Up: Linear algebra
Previous: The LinearMatrixConsistency procedure
Contents
Jean-Pierre Merlet
2012-12-20