



Next: The GerschgorinConsistency procedure
Up: Linear algebra
Previous: The SpectralRadiusConsistency procedure
Contents
This procedure should be used in conjunction with RegularMatrix.
It should be used only if the matrix includes rows or columns in which
a variable appears with degree 1 in at least 2 elements of a row
or a column. Its syntax is:
LinearMatrixConsistency(A,VAR,vars,row,context,rohn,
Func,FuncKA,FuncAK,name)
The parameters are:
- A: the considered matrix
- VAR: a list of the variable name that appears in the
matrix
- vars: a list of variable names that appears linearly in
the row or column of A
- row: 1 if the procedure look at the row of A, 2
for the column
- context: see description
- rohn: 1 if the Rohn consistency procedure is used in the
program
- Func, FuncKA, FuncAK: the name of C++ procedures to
compute respectively the matrix, the left conditioned matrix and the
right conditioned matrix. If this procedure is used in conjunction with
RegularMatrix these names are we have
Func="F", FuncKA="AKA", FuncAK="AAK".
- name: the name of the C++ procedure that will be created
in the file name.C
Linearity has to be understood in a very loose sense. For example if a
row of the matrix is
x xy x+y
this row may be considered as linear in x in which case we have
3 linear elements in the row. If the row is considered as linear in
y we have 2 linear elements in the row.
Note that the linearity is checked according to the order provided in
Vars.
This procedure may be used for the matrix A,
the conditioned matrix KA or the conditioned matrix AK.
Context is used to indicate the choice according to the following
code:
- 0: for A only
- 1: for KA only
- 2: for AK only
- 3: for A, KA, KA
- 4: for AK, KA
- 5: for A, KA
- 6: for A, AK
The complexity of this procedure is approximately
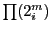 where
where 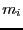 is is the number of linear terms in
the elements of row or column i of A. Hence it should not be
be used with a large Vars. The use of Rohn matrix may also
be expensive as it requires to calculate
is is the number of linear terms in
the elements of row or column i of A. Hence it should not be
be used with a large Vars. The use of Rohn matrix may also
be expensive as it requires to calculate 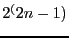 scalar
determinant, with
scalar
determinant, with 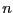 the dimension of the matrix A.
the dimension of the matrix A.
For example we may use
LinearMatrixConsistency(A,[x,y],[x],1,5,"F","AKA","","Simp"):
In this example we will consider the row of matrix A and its
elements that are linear in x. The procedure will be used for
both the matrix A and the conditioned matrix KA (hence
this procedure should be used with the parameter cond of RegularMAtrix set to 1 or 3.
Note that we assume here that the conditioning matrix is
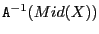 .
.




Next: The GerschgorinConsistency procedure
Up: Linear algebra
Previous: The SpectralRadiusConsistency procedure
Contents
Jean-Pierre Merlet
2012-12-20