



Next: Solving univariate polynomial numerically
Up: Implementation
Previous: Implementation
Contents
Example
The program Test_Solve_UP is a general test program which
enable to solve univariate polynomial whose coefficients are given in
a file by increasing power of the unknown.
We use as example the Wilkinson polynomial of degree  where
where 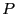 :
:
It is well known that this polynomial is extremely
ill-conditioned. For 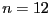 the coefficient of
the coefficient of 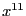 is 78. But if
we modify this coefficient by
is 78. But if
we modify this coefficient by 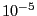 there is a big change in the
roots, 4 of them becoming complex [4].
The general procedure leads to reasonable
accurate result up to
there is a big change in the
roots, 4 of them becoming complex [4].
The general procedure leads to reasonable
accurate result up to 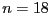 . At
. At 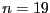 although Kantorovitch theorem has determined interval solutions that
indeed contain all the solutions,
Newton method is unable to provide an
accurate estimate of this root due to numerical errors.
although Kantorovitch theorem has determined interval solutions that
indeed contain all the solutions,
Newton method is unable to provide an
accurate estimate of this root due to numerical errors.
For 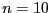 and if we are looking for the roots in the interval
[0,2] the computation time is 90ms, for
and if we are looking for the roots in the interval
[0,2] the computation time is 90ms, for 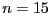 190ms and 330ms for
190ms and 330ms for 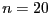 .
For the fast algorithm these times are: 10ms, 20ms, 30 ms
Note that the best classical solving algorithm start to give
inaccurate results for
.
For the fast algorithm these times are: 10ms, 20ms, 30 ms
Note that the best classical solving algorithm start to give
inaccurate results for 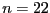 (between 12.5 and 18.5 the interval
analysis algorithm finds the roots
13.424830, 13.538691, 15.477653, 15.498664, 17.554518, 17.553513)
and give imaginary roots for
(between 12.5 and 18.5 the interval
analysis algorithm finds the roots
13.424830, 13.538691, 15.477653, 15.498664, 17.554518, 17.553513)
and give imaginary roots for 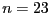 .
.




Next: Solving univariate polynomial numerically
Up: Implementation
Previous: Implementation
Contents
Jean-Pierre Merlet
2012-12-20
![]() where
where ![]() :
:
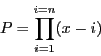
![]() and if we are looking for the roots in the interval
[0,2] the computation time is 90ms, for
and if we are looking for the roots in the interval
[0,2] the computation time is 90ms, for ![]() 190ms and 330ms for
190ms and 330ms for ![]() .
For the fast algorithm these times are: 10ms, 20ms, 30 ms
Note that the best classical solving algorithm start to give
inaccurate results for
.
For the fast algorithm these times are: 10ms, 20ms, 30 ms
Note that the best classical solving algorithm start to give
inaccurate results for ![]() (between 12.5 and 18.5 the interval
analysis algorithm finds the roots
13.424830, 13.538691, 15.477653, 15.498664, 17.554518, 17.553513)
and give imaginary roots for
(between 12.5 and 18.5 the interval
analysis algorithm finds the roots
13.424830, 13.538691, 15.477653, 15.498664, 17.554518, 17.553513)
and give imaginary roots for ![]() .
.