



Next: Improving the evaluation using
Up: Mathematical background
Previous: Mathematical background
Contents
Using the monotonicity
For a given box we will compute the jacobian matrix using
interval analysis. Each row 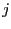 of this interval matrix enable to get some
information of the corresponding function
of this interval matrix enable to get some
information of the corresponding function 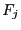 .
.
- if the i-th column of the j-th row is an interval which is
strictly negative or strictly positive, then
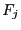 is monotonic with
respect to the unknowns
is monotonic with
respect to the unknowns 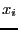
- if the i-th column of the j-th row is equal to 0, then function
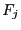 does not depend on the variable
does not depend on the variable 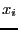
In the first case the minimal and maximal value of 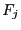 will be
obtained either for
will be
obtained either for
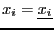 or
or
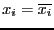 and we are able to define the value of
and we are able to define the value of 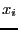 to get
successively the minimal and maximal value as we know the sign of the
gradient. But this procedure has to be implemented recursively. Indeed
we have previously computed the jacobian matrix for
to get
successively the minimal and maximal value as we know the sign of the
gradient. But this procedure has to be implemented recursively. Indeed
we have previously computed the jacobian matrix for
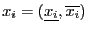 but now
but now
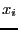 have a fixed value: hence a component
have a fixed value: hence a component 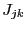 of the j-th row which
for
of the j-th row which
for
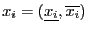 was such that
was such that
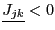 and
and
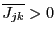 may now be a strictly positive or negative
intervals. Consequently the minimal and maximal value will be obtained
for some combination of
may now be a strictly positive or negative
intervals. Consequently the minimal and maximal value will be obtained
for some combination of 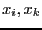 in the two sets
in the two sets
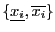 and
and
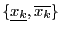 . Bus as
. Bus as 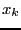 has now a fixed value
some other component of
has now a fixed value
some other component of 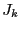 may become strictly negative or
positive...
may become strictly negative or
positive...
The algorithm for computing a sharper evaluation of 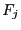 is:
is:
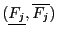 =Evaluate
=Evaluate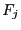 (
(
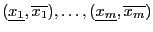 )
)
- compute
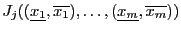
- let
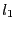 be the number of components of
be the number of components of 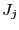 such that
such that
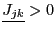 or
or
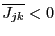 and let
and let
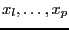 be the variables for which this occur
be the variables for which this occur
- if
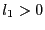
loop:
for all combination of
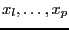 in the set
in the set
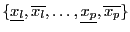 :
:
- if
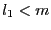
- compute
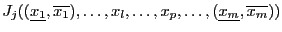
- let
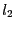 be the number of components of
be the number of components of 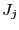 such that
such that
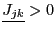 or
or
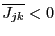
- if
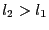 , then
, then
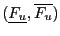 =Evaluate
=Evaluate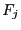 (
(
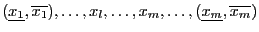 )
)
- otherwise
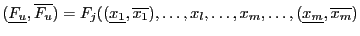 )
)
- if this is the first estimation of
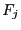 then
then 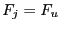
- otherwise
- otherwise
-
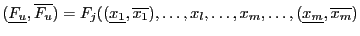 )
)
- if this is the first estimation of
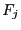 then
then 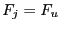
- otherwise
- end loop:
- otherwise
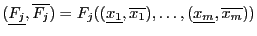
- return
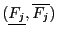
This procedure has to be repeated for each 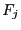 .
.




Next: Improving the evaluation using
Up: Mathematical background
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20
![]() of this interval matrix enable to get some
information of the corresponding function
of this interval matrix enable to get some
information of the corresponding function ![]() .
.
![]() is:
is:
![]() =Evaluate
=Evaluate![]() (
(
![]() )
)