Example 3

Next: Example 4 Up: Examples and Troubleshooting Previous: Example 2

La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de COPRIN

COPRIN home page

La page "Présentation" de l'INRIA

INRIA home page

Example 3

This example is derived from example 2. We notice that in the three functions of example 2 the second degree terms of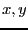

are for all functions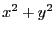

. Thus by subtracting the first function to the second and third we get a linear system in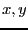

. This system is solved and the value of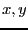

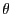are substituted in the first function. We get thus a system of one equation in the unknown $\theta$ (see section 15.1.2). The roots of this equation are 0,-0.806783438. The test program is Test_Solve_General2. The IntervalFunction is written as:

 
INTERVAL_VECTOR IntervalTestFunction (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL_VECTOR xx(1);
xx(1)=11092.0+(-25912.0+(19660.0-4840.0*Cos(in(1)))*Cos(in(1)))*Cos(in(1))+(
-508.0+(3788.0-1600.0*Cos(in(1)))*Cos(in(1)))*Sin(in(1));
return xx;
}

This program is implemented under the name Test_Solve_General2. With epsilonf=0 and epsilon=0.001 we get the solution intervals, using 32 boxes:

$\begin{displaymath} \theta=[-0.0007669904,0]~~~ \theta=[-0.8068739,-0.8061069] \end{displaymath}$

for whatever order. If we use epsilon=0 and epsilonf=0.1 we get, using 50 boxes:

$\begin{eqnarray*} && \theta=[-0.806784012741056,-0.806781016684830]\\ && \theta=[-4.793689962142628e-05,0] \end{eqnarray*}$

In both cases the solution intervals contain the roots of the equation.