Box reduction

Let Sol be a solution of a system that has been found in the box B while the algorithm was processing a list of boxes BOX. It is of interest to treat the box and the list of boxes in such way that Sol is no more included in the set of boxes i.e. to have in the list of boxes only the complementary of each box with respect to the box Sol. Note that for a problem with 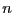$n$ unknowns this complementary may be described by up to 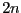$2n$ boxes.

This may be obtained by using:

int Sol_Reduction(int Dimension,int Dimension_Eq,
                INTERVAL_MATRIX &BOX,
               INTERVAL_VECTOR &B, INTERVAL_VECTOR &Sol,
               int *nb,int type,
               int (* Simp_Proc)(INTERVAL_VECTOR &))

where

• nb: the total number of boxes in the list BOX
• type: allow to create at most type new boxes that will be appended to BOX
• Simp_Proc: a simplification procedure for the system

This algorithm will return -1 if the solution box covers completely the box B. Note that this algorithm may create new boxes but only ALIAS_Allows_N_New_Boxes are allowed to be created (with a default value of 2). A similar procedure exists when gradient boxes have also to be stored:

 
int Sol_Reduction(int Dimension_Var,int Dimension_Eq,
  INTERVAL_MATRIX &BBOX,
  INTERVAL_MATRIX &GBBOX,
  INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &), 
  INTERVAL_VECTOR &P, INTERVAL_VECTOR &PP1,
  int current_box,int *nb_box,
  int nb_max_box,int type,
  int (* Simp_Proc)(INTERVAL_VECTOR &))

where

• GBBOX: the gradient boxes
• current_box: the number of the current box
• nb_box: the total number of boxes
• nb_max_box: the maximal number of new boxes that can be created
• type: if nb_max_box is lower than 2Dimension_Var then the full complementary boxes cannot be generated. Hence the boxes that will be generated will still have an intersection with PP1. But the set of generated boxes will depend on the order in which the variables are considered when generating the new boxes. type allows one to specify this order. If set to 1 the algorithm will consider the variables according to the width of their range, the largest first. If set to 2 it will consider the variable according to their influence in the sense of the smear function (see section 2.4.1.3. For any other value the variables will be considered in the order of their definition.

Note that in the Solve_General_Gradient_Interval and Solve_General_JH_Interval we use for nb_max_box the value of ALIAS_Allows_N_New_Boxes (with a default value of 2) and for type the value of ALIAS_Type_N_New_Boxes (default value of 0)