



Next: Example 2
Up: Examples
Previous: Examples
Contents
Consider the equation:
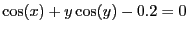 which defines a curve in the
which defines a curve in the 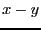 plane on which you want to
determine the closest point to the origin when
plane on which you want to
determine the closest point to the origin when 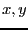 lie in the range
lie in the range
![$[-\pi,\pi]$](img275.png) . This leads to trying to
find the minimum of the function
. This leads to trying to
find the minimum of the function 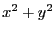 under the constraint
under the constraint
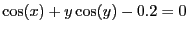 .
.
The procedure for the interval evaluation of the 2 functions will be
written as:
INTERVAL_VECTOR IntervalTestFunction (int l1,int l2,INTERVAL_VECTOR & in)
// interval valued test function
{
INTERVAL x,y;
INTERVAL_VECTOR xx(2);
x=in(1);
y=in(2);
if(l1==1)
xx(1)=Cos(x)+y*Sqr(Cos(y))-0.2;
if(l1<=2 && l2>=2)
xx(2)=Sqr(x)+Sqr(y);
return xx;
}
while the main program may be written as:
int main()
{
int Iterations, Dimension,Dimension_Eq,Num,i,j,precision;
double Accuracy,Accuracy_Variable;
INTERVAL_MATRIX SolutionList(2,2);
INTERVAL_VECTOR TestDomain(2),F(2),P(2),H(2);
INTEGER_VECTOR Type(2);
INTERVAL Optimum;
REAL pi;
pi=Constant::Pi;
Dimension_Eq=2;Dimension=2;
TestDomain(1)=INTERVAL(-pi,pi);TestDomain(2)=INTERVAL(-pi,pi);
cerr << "Number of iteration = "; cin >> Iterations;
cerr << "Accuracy on Function = "; cin >> Accuracy;
Type(1)=0;Type(2)=-2;
Accuracy=0;
Num=Minimize_Maximize(Dimension,Dimension_Eq,Type,
IntervalTestFunction,TestDomain,Iterations,Accuracy_Variable,
Accuracy,0,Optimum,SolutionList);
if(Num<0)
{
cout << "The procedure has failed, error code:"<<Num<<endl;
return 0;
}
cout<<"Optimum:"<<Optimum<<" obtained at"<<endl;
for(i=1;i<=Num;i++)
{
cout << "x=" << SolutionList(i,1) <<endl;
cout << "y=" << SolutionList(i,2) <<endl;
}
return 0;
}
The Minimize_Maximize
and Minimize_Maximize_Gradient procedures will return the
same numerical results but the number of boxes will change.
The
results obtained for a full bisection,
the MAX_MIDDLE_FUNCTION_ORDER
and according to the accuracy epsilonf and the storage mode
(either direct (DSM) or reverse (RSM), see section 2.3.1.2) are
presented in the
following table (the number of boxes for the
Minimize_Maximize_Gradient procedure is indicated in
parenthesis):
| epsilonf |
Minimum |
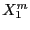 |
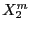 |
boxes |
|
0.01, DSM |
[1.12195667, 1.12195667] |
[-0.944932,-0.4786] |
[-0.944932,-0.4786] |
76 (36) |
|
0.01, RSM |
[1.12195667, 1.12195667] |
[-0.944932,-0.4786] |
[-0.944932,-0.4786] |
59 (37) |
|
0.001, DSM |
[1.1401661,1.1401661] |
[-0.954903,-0.477835] |
[-0.954903,-0.477835] |
201 (75) |
|
0.001, RSM |
[1.1401661,1.1401661] |
[-0.954903,-0.477835] |
[-0.954903,-0.477835] |
148 (67) |
|
0.000001, DSM |
[1.14223267,1.14223267] |
[-0.957596,-0.474596] |
[-0.957596,-0.474596] |
5031 (2041) |
|
0.000001, RSM |
[1.14223267,1.14223267] |
[-0.957596,-0.474596] |
[-0.957596,-0.474596] |
4590 (2164) |




Next: Example 2
Up: Examples
Previous: Examples
Contents
Jean-Pierre Merlet
2012-12-20