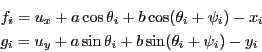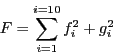Next: Examples
Up: Implementation
Previous: General principle
Contents
The variable table
Assume now that you have chosen a mixed bisection in which the
bisection is applied on 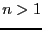 variables. The procedure will choose the
bisected variables using, for example, the smear function. But in some
cases it may be interesting to guide the bisection: for example if we
know that subsets of the variables have a strong influence
on the extremal value of the
optimum function it may be interesting to indicate that as soon as the
smear function has led to bisecting one variable in a given subset it
may be good to bisect also the other variables in the subset. For
example consider the following functions:
variables. The procedure will choose the
bisected variables using, for example, the smear function. But in some
cases it may be interesting to guide the bisection: for example if we
know that subsets of the variables have a strong influence
on the extremal value of the
optimum function it may be interesting to indicate that as soon as the
smear function has led to bisecting one variable in a given subset it
may be good to bisect also the other variables in the subset. For
example consider the following functions:
where
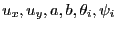 are unknowns and
are unknowns and 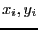 are given. Consider now the optimum function
are given. Consider now the optimum function 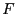 :
:
which has 24 unknowns. But clearly each subset
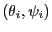 has a strong influence on the minimum of
has a strong influence on the minimum of 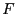 . Hence if one of the
. Hence if one of the
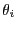 is bisected it may be interesting to bisect also
is bisected it may be interesting to bisect also
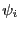 . This may be done by setting the flag
ALIAS_Guide_Bisection to 1
and using the
variables table:
for a problem with
. This may be done by setting the flag
ALIAS_Guide_Bisection to 1
and using the
variables table:
for a problem with 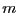 unknowns the variables table
unknowns the variables table 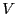 is an array of
size
is an array of
size 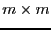 and a 1 in
and a 1 in 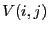 indicates that if the variable
indicates that if the variable
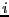 is bisected then the variable
is bisected then the variable 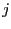 should be also bisected. In
ALIAS the variables table is implemented under the name
ALIAS_Bisecting_Table.
It is the responsibility of the user to
clear this array and update it as in the following example:
should be also bisected. In
ALIAS the variables table is implemented under the name
ALIAS_Bisecting_Table.
It is the responsibility of the user to
clear this array and update it as in the following example:
Resize(ALIAS_Bisecting_Table,24,24);
Clear(ALIAS_Bisecting_Table);
ALIAS_Bisecting_Table(1,2)=1;
ALIAS_Bisecting_Table(2,1)=1;
ALIAS_Bisecting_Table(3,4)=1;
ALIAS_Bisecting_Table(4,3)=1;




Next: Examples
Up: Implementation
Previous: General principle
Contents
Jean-Pierre Merlet
2012-12-20
![]() variables. The procedure will choose the
bisected variables using, for example, the smear function. But in some
cases it may be interesting to guide the bisection: for example if we
know that subsets of the variables have a strong influence
on the extremal value of the
optimum function it may be interesting to indicate that as soon as the
smear function has led to bisecting one variable in a given subset it
may be good to bisect also the other variables in the subset. For
example consider the following functions:
variables. The procedure will choose the
bisected variables using, for example, the smear function. But in some
cases it may be interesting to guide the bisection: for example if we
know that subsets of the variables have a strong influence
on the extremal value of the
optimum function it may be interesting to indicate that as soon as the
smear function has led to bisecting one variable in a given subset it
may be good to bisect also the other variables in the subset. For
example consider the following functions: