Next: The variable table
Up: Order
Previous: Order
Contents
During the bisection process new boxes will be created and
stored in the list. But we want to order these new boxes so
that the procedure will consider first the most promising box.
The ordering is based on an evaluation index, the new boxes
being stored using an increasing order of the index (the
box with the lowest index will be stored first).
The flag Order indicate which index is used:
indexMAXCONSTRAINTFUNCTION@MAX_CONSTRAINT_FUNCTION
- MAX_FUNCTION_ORDER: let
![$[\underline{F_i},\overline{F_i}]$](img740.png) be the interval evaluation of
the optimum equation
be the interval evaluation of
the optimum equation 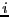 . The index is obtained as
. The index is obtained as
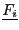 for a minimization problem
and
for a minimization problem
and
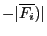 for a maximization problem,
for a maximization problem,
- MAX_CONSTRAINT_FUNCTION: same than MAX_FUNCTION_ORDER if there is only one equation in the system.
Otherwise:
- if there are equality constraints use the
MAX_FUNCTION_ORDER index
- if there are only inequality constraints and if they all
hold for all the new boxes, then the index is the lower bound
of the optimum function for a minimization problem and the upper bound
for a maximization problem.
- if there are only inequality constraints and none of the
new boxes satisfied them all: the index is the upper bound
of the inequality for the constraint of type
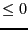 and the absolute
value of the lower bound for the constraint of type
and the absolute
value of the lower bound for the constraint of type 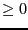
- if there are only inequality constraints and they are all
verified only for some of the new boxes, then the index will be
calculated in such way that the boxes
satisfying the constraints will be stored first according to the value
of the lower or upper bound of the optimum function. Then will be
stored the boxes not satisfying the constraints according to
the index described in the previous item
- MAX_MIDDLE_FUNCTION_ORDER: let
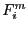 be the value of
the function
be the value of
the function 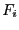 computed for the middle point of the box.
The index is the absolute value of
computed for the middle point of the box.
The index is the absolute value of 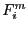




Next: The variable table
Up: Order
Previous: Order
Contents
Jean-Pierre Merlet
2012-12-20
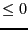 and the absolute
value of the lower bound for the constraint of type
and the absolute
value of the lower bound for the constraint of type