



Next: Implementation
Up: Optimization
Previous: Definition of a minimum
Contents
A first method to find all the solutions of an optimum problem
is to consider the system of derivative equations and find its root
(eventually under the given constraints): this may be done with the
solving procedures described in a previous chapter. Hence we have
implemented an alternative method which is able to work even if the
optimum function has, globally or locally, no derivatives.
This method is implemented as a special case of the general
solving procedures. The only difference is that the procedure maintains
a value for the current optimum: during the bisection process we
evaluate the optimum function for each new box and reject those
that are not compatible with the current optimum.
Two types of method enable to solve
an optimization problem:
- a method which need only a procedure for evaluating
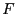 ,
,
- a method which need a procedure for evaluating
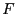 and a
procedure for evaluating its gradient,
and a
procedure for evaluating its gradient,
Note that with the first method none of the function needs to be
differentiable while for the other one not all the functions in the
set 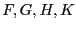 must be differentiable: only one function in the set
has to be differentiable.
must be differentiable: only one function in the set
has to be differentiable.
For the first method
we update the current optimum by computing the optimum
function value at the middle point of the box. For the
method with the gradient a local optimizer based on the steepest
descent
method is also used if there is
only one equation to be minimized or if there are only inequalities
constraints. The local optimizer works in 2 steps: first a rough
optimization and then a more elaborate procedure if the result of the
first step is better than a fixed threshold defined by the global
variable ALIAS_Threshold_Optimiser
whose default value is 100.
Additionally if an extremum 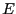 has been already determined
the local optimizer (which may computer intensive)
is called only if the function value
has been already determined
the local optimizer (which may computer intensive)
is called only if the function value 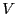 at the middle
point is such that for a maximum
at the middle
point is such that for a maximum
 and
and
 for a minimum, where ALIAS_LO_A and ALIAS_LO_B are global variables with default
value 0.9 and 1.1.
for a minimum, where ALIAS_LO_A and ALIAS_LO_B are global variables with default
value 0.9 and 1.1.




Next: Implementation
Up: Optimization
Previous: Definition of a minimum
Contents
Jean-Pierre Merlet
2012-12-20
![]() has been already determined
the local optimizer (which may computer intensive)
is called only if the function value
has been already determined
the local optimizer (which may computer intensive)
is called only if the function value ![]() at the middle
point is such that for a maximum
at the middle
point is such that for a maximum
![]() and
and
![]() for a minimum, where ALIAS_LO_A and ALIAS_LO_B are global variables with default
value 0.9 and 1.1.
for a minimum, where ALIAS_LO_A and ALIAS_LO_B are global variables with default
value 0.9 and 1.1.