



Next: Implementation
Up: Regularity of matrix with
Previous: Regularity of matrix with
Contents
Let assume that a parametric matrix has rows (or columns) in which
some elements depend linearly on some of the unknowns. Let consider
the set 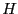 of
interval matrices obtained as follows:
of
interval matrices obtained as follows:
- for row
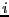 let
let 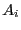 be the elements that depend linearly on
the unknowns
be the elements that depend linearly on
the unknowns
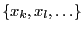 (called the linear unknowns)
(called the linear unknowns)
- construct all possible rows for row
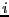 by fixing the linear
unknowns either to their minimum or maximum
by fixing the linear
unknowns either to their minimum or maximum
- construct the set
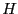 by taking all possible combinations of all
rows
by taking all possible combinations of all
rows
It can be then shown that if all the matrices in 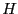 have their
determinants of the same sign, then the set of parametric matrices
does not include any singular matrix. This test is more powerful than
the test proposed by Rohn (see section 7.4.2) as it takes more
into account the structure of the parametric matrix.
have their
determinants of the same sign, then the set of parametric matrices
does not include any singular matrix. This test is more powerful than
the test proposed by Rohn (see section 7.4.2) as it takes more
into account the structure of the parametric matrix.
Jean-Pierre Merlet
2012-12-20