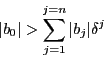Let ![]() be a polynomial and be maxroot the maximal modulus of
the root of
be a polynomial and be maxroot the maximal modulus of
the root of ![]() . From
. From ![]() we may derive a the unitary polynomial
we may derive a the unitary polynomial ![]() such that the
roots of
such that the
roots of ![]() have a modulus lower or equal to 1 and if
have a modulus lower or equal to 1 and if ![]() is a root
of
is a root
of ![]() then maxroot
then maxroot![]() is a root of
is a root of ![]() .
.
Let
![]() which may also be written as
which may also be written as
![]() where
where ![]() is some fixed point.
is some fixed point.
Let a range ![]() for
for ![]() and let
and let ![]() be the mid point of the
range. We consider the square in the complex plane centered at
be the mid point of the
range. We consider the square in the complex plane centered at ![]() and whose edge length is
and whose edge length is ![]() . Let
. Let ![]() be the length of the
half-diagonal of this square.
If
be the length of the
half-diagonal of this square.
If