



Next: Possible parameters values for
Up: Parametric polynomials and eigenvalues
Previous: Parametric polynomials and eigenvalues
Contents
Minimal and maximal real roots of a parametric polynomial
The purpose here is to determine the minimal and maximal values of the
set of real roots of the the set of polynomials, when the parameters
are bounded. There may be eventually also constraints on the
parameters.
The algorithm is implemented as:
int ALIAS_Min_Max_EigenValues(int Degree,
int Nb_Parameter,
INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &),
int Nb_Constraints,
INTEGER_VECTOR &Type_Eq,
int (* TheMatrix)(INTERVAL_VECTOR &, INTERVAL_MATRIX &),
int Has_Matrix,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
int *Has_Gradient,
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL & TheDomain,
INTERVAL_VECTOR & TheDomain_Parameter,
int Type,int Nb_Points,int Use_Solve,int rand,
int M,
double Accuracy_Variable,double Accuracy,double AccuracyM,
INTERVAL &Lowest_Root,INTERVAL &Highest_Root,
INTERVAL_MATRIX &Place,int Stop,double *Seuil,
int (* Solve_Poly)(double *, int *,double *),
int (* Simp_Proc)(INTERVAL_VECTOR &))
where the arguments are:
- Degree: degree of the polynomial
- Nb_Parameter: number of parameters appearing in the
coefficients
- TheCoeff: a procedure that take as input an interval
vector and returns the interval value of the coefficients of the
polynomial. The elements of the input interval vector are first a
range for the unknown in the polynomial, then the ranges for the Nb_Parameter parameters
- Nb_Constraints: the number of constraints expression that
constraints the parameters
- Type_Eq: type of the constraints expressions (0 for
equality, -1 for inequality of type
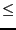 0, 1 for inequality of type
0, 1 for inequality of type
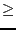 0)
0)
- TheMatrix: the polynomial may be the characteristic
polynomial of a matrix
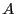 . This argument is a procedure that takes
as first argument the
same interval vector as TheCoeff and returns in the second
argument the interval component of
. This argument is a procedure that takes
as first argument the
same interval vector as TheCoeff and returns in the second
argument the interval component of 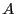 . This procedure must return 1
if the components have been successfully calculated, -1 otherwise
. This procedure must return 1
if the components have been successfully calculated, -1 otherwise
- Has_Matrix: this flag must be set to 0 except if the
polynomial is the the characteristic
polynomial of a matrix in which case it must be set to 1 (2 if the
matrix is symmetrical)
- IntervalFunction: a function which return the interval
vector evaluation of the constraints and of the polynomial, the last
component of the vector being the interval evaluation of the
polynomial. This procedure must be written in ALIAS standard form, see
note 2.3.4.3
- Has_Gradient: an array of integer that indicates if the
derivatives of the expression are available. Only the first element is
used for now with the following value:
- 0: no derivative available
- 1: only the derivatives of the constraints are
available, not the one of the polynomial
- 2: all derivatives are available
- Gradient:a procedure which returns the Jacobian matrix of
the expression for given values of the unknowns written in standard
ALIAS form (see note 2.4.2.2)
- TheDomain: range for the polynomial unknown. This range
must be large and is automatically adjusted during the calculation
- TheDomain_Parameter: the ranges for the parameters
- Type: 0 for finding only the minimum of the real root, 1
to find only the maximal root and 2 to find both
- Nb_Points: to estimate the minimal and maximal real root
the algorithm compute the root of the polynomial at some given points
for which the parameters have a fixed value. This value give the
number of points where this procedure is used, it must be at least 1.
- Use_Solve: if this parameter is 1 or 3, then for each box
we try to determine bounds for the real roots using algebraic
geometry. If it is 2 or 3 then for each box we solve numerically the
polynomial for
some specific values of the parameters to update the minimum and
maximum. If the value is 0 or 1 we will assume that a root of a
polynomial is obtained when the width of the box is lower than Accuracy_Variable and the width of the evaluation of the polynomial
is lower than Accuracy. If the confidence in the routine that
solve numerically a polynomial is low the best choice is 1 otherwise
the best choice is 3
- rand: every rand iteration the algorithm will
consider that the current box is the one in the list that has the
largest width. Such random permutation may allow to determine the
minimal and maximal real root more quickly. This number must be
neither
too low (otherwise the maximal memory available may be exceeded) nor
too large (otherwise the algorithm may focus on some part of the
search space while the optimum is located in another part). A good
compromise is 100.
- M: the maximum number of boxes which may be
stored. See the note 2.3.4.5
- accuracy_Variable: the maximal width of the range of the
polynomial unknown to be a solution, see the
note 2.3.4.6
- Accuracy: the maximal width of the polynomial evaluation for
a solution, see the
note 2.3.4.6
- AccuracyM: the accuracy with which the optimum is
determined. The absolute value of the difference between the real
optimum and the calculated one should not
exceed this value
- Lowest_Root, Highest_Root: point interval
giving the minimal and maximal
real root
- Place: the value of the parameters for which the optimum
is obtained: the first line is for the minimum and the second line for
the maximum
- Stop, Seuil: if Stop is set to 1
- when looking for a minimum only the procedure exit as
soon as a minimum lower than Seuil[0] has been found
- when looking for a maximum only the procedure exit as
soon as a maximum greater than Seuil[1] has been found
- when looking both for a minimum and a maximum the
procedure exit as a minimum lower than Seuil[0]
OR a maximum greater than Seuil[1] has been found
If Stop is set to 2 when looking both for a minimum and a maximum the
procedure exit as a minimum lower than Seuil[0]
AND a maximum greater than Seuil[1] has been found (otherwise as
the same behavior than 1)
- Solve_Poly: a procedure that compute the real roots of a
polynomial. It takes as argument the coefficients of the polynomial, a
pointer to an integer that is initially the degree of the polynomial
and the real roots are stored in the last argument. This
procedure returns the number of real roots or -1 if the computation
has failed. ALIAS provides as possible procedure ALIAS_Solve_Poly.
- Simp_Proc: a user-supplied procedure that take as input
the current box and may proceed to some reduction of
the width of the box or even determine that there is no
solution for this box, in which case it should return
-1.
The confidence in this procedure is at the same level than the
confidence in the numerical algorithm that solve a polynomial.
The return code is:
- 1: algorithm has succeeded
- 0: result is not guaranteed
- -1: algorithm has failed, not enough memory
- -2: largest root of the polynomial lower than the given lower
bound
- -3: smallest root of the polynomial larger than the given upper
bound
- -4: error in the type of the equations
- -5: error, more than one function to optimize
- -100: in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
- -150: ALIAS_Delta3B or
ALIAS_Max3B have not the right dimension Nb_Parameter+1
- -200: one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
- -300: one of the value of ALIAS_SubEq3B is not 0 or 1
- -1000: Single_Bisection has an incorrect value
- -1500: Degree is lower than 0
- -2000: Nb_Parameter is lower or equal to 0
- -3000: we use the full bisection mode and the problem has
more than 10 unknowns
- -3500: Nb_Constraints is lower than 0
- -4000: Type not between 0 and 2
- -4500: Stop_First_Sol not between 0 and 2
- -5000: Use_Solve not between 0 and 4
- -6000: Place has not 2 rows or Nb_Parameter+1
columns
- -6500: the initial estimate have incompatible lower and upper
bound
The possible bisection mode are:
- 1: if the polynomial parameter has a value that is better than
the current optimum, then this variable is bisected otherwise mode 1
of section 2.4.1.3
- 2: mode 1 of section 2.4.1.3 if the gradient is not available
- 3,4: mode 1 of section 2.4.1.3
- 5: mode 5 of section 2.4.1.3
For mode 2 if the gradient is available and if the polynomial parameter
has a value that is better than
the current optimum, then this variable is bisected otherwise we use
the smear function to determine the bisected variable.




Next: Possible parameters values for
Up: Parametric polynomials and eigenvalues
Previous: Parametric polynomials and eigenvalues
Contents
Jean-Pierre Merlet
2012-12-20