



Next: Implementation
Up: Sturm method
Previous: Sturm method
Contents
Let a polynomial  and define
and define 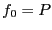 ,
, 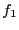 be the first derivative
of
be the first derivative
of  . Then define the sequence
. Then define the sequence
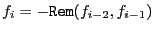 where Rem is the remainder of the division of
where Rem is the remainder of the division of 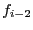 by
by
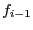 . If
. If  is the degree of
is the degree of  the last element in the
sequence will be
the last element in the
sequence will be 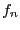 . Assume now that we are looking for the number
of distinct roots of
. Assume now that we are looking for the number
of distinct roots of  in the interval
in the interval ![$[a,b]$](img605.png) with
with
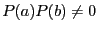 .
We build two sequences:
.
We build two sequences:
Let 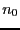 be the number of change of sign in the first sequence and
be the number of change of sign in the first sequence and
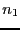 be the number of change of sign in the second sequence. Then the
number of distinct real roots of
be the number of change of sign in the second sequence. Then the
number of distinct real roots of  in the interval
in the interval ![$[a,b]$](img605.png) is
is
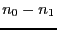 [14] if
[14] if
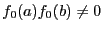 .
Note that a multiple roots count only for one root with this method.
.
Note that a multiple roots count only for one root with this method.
The drawback of Sturm method is that the absolute value of the
coefficients increase quickly when computing the sequence. Numerical
rounding errors may then affect the result. The alternate method of
Budan-Fourier (see section 5.5.2) is less sensitive to rounding
errors
although it provides less information than Sturm method.




Next: Implementation
Up: Sturm method
Previous: Sturm method
Contents
Jean-Pierre Merlet
2012-12-20