



Next: Implementation
Up: Budan-Fourier method
Previous: Budan-Fourier method
Contents
Budan-Fourier algorithm is a simple method which enable to determine
easily some information on the number of root of a given univariate
polynomial within a given interval. Let  the polynomial:
the polynomial:
and 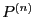 its n-th derivative. Let the interval
its n-th derivative. Let the interval
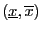 the
interval in which we are looking for roots. We assume that
the
interval in which we are looking for roots. We assume that
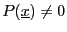 ,
,
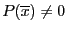 and
and 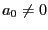 .
We construct the sequence
.
We construct the sequence
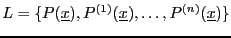 from which we exclude the 0 element. Similarly we construct the
sequence
from which we exclude the 0 element. Similarly we construct the
sequence
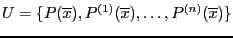 (a special treatment has to be applied for the zero element of
(a special treatment has to be applied for the zero element of 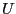 ,
see [13]). Let
,
see [13]). Let 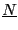 the number of change of sign
in
the number of change of sign
in 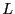 and
and 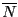 the number of change of sign in
the number of change of sign in 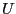 . Then
the number of real roots of
. Then
the number of real roots of  in
in
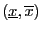 , counted with their order
of multiplicity, is
, counted with their order
of multiplicity, is
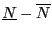 or lower than this number by an even
number.
or lower than this number by an even
number.
Jean-Pierre Merlet
2012-12-20