



Next: Implementation
Up: Miranda theorem
Previous: Miranda theorem
Contents
Let a system 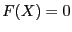 with
with
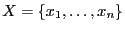 . Let us consider a
ball
. Let us consider a
ball
![${\cal B}=\{[\underline{x_1},\overline{x_1}],\ldots,[\underline{x_n},\overline{x_n}]$](img453.png) for
for 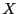 and define
and define
for 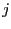 in
in ![$[1,n]$](img11.png) . If
. If
or if
then 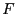 has at least one zero in
has at least one zero in 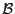 [15].
[15].
Jean-Pierre Merlet
2012-12-20
![]() with
with
![]() . Let us consider a
ball
. Let us consider a
ball
![]() for
for ![]() and define
and define
![\begin{eqnarray*}
&&[X]_j^+ = \{X \in {\cal B}~{\rm such~that}~x_j=\overline{x_j...
..._j^- = \{X \in {\cal B}~{\rm such~that}~x_j=\underline{x_j}\}\\
\end{eqnarray*}](img454.png)