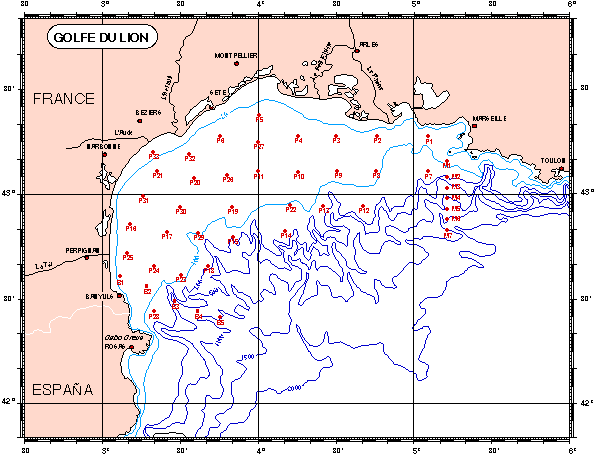
Figure II.1: Géographie et topographie du Golfe du Lion
Couplage d’un modèle hydrodynamique à un modèle de croissance algale pour décrire l’environnement d’une cellule phytoplanctonique
MEMOIRE DE FIN D’ETUDES - Ecole des Métiers de l’Environnement
MAUGUIN – Grégory
Introduction
La mission qui m’a été confiée s’inscrit dans le
cadre du projet SEMPO (Simulateur d’Environnement Marin Piloté par
Ordinateur). A long terme, le projet SEMPO ambitionne d’affiner l’estimation
des flux de Carbone à l’interface océan-atmosphère.
La quantification de ceux-ci inscrit ce projet au centre des grandes
problématiques liées à l’effet de serre dont
l’objectif global est d’estimer la vitesse d’élévation du
taux de Carbone dans l’atmosphère terrestre. La connaissance de
cette donnée permettrait alors de mesurer l’importance des modifications
climatiques qui pourraient se produire à l’échelle planétaire,
ainsi que la rapidité à laquelle de tels changements seraient
susceptibles de survenir.
La première étape d’un tel projet consistait à
développer un modèle informatique prenant en compte, les
aspects hydrodynamiques, mais aussi ceux liés à l’activité
biologique du phytoplancton, propres à l’écosystème
océan. Un modèle hydrodynamique (baptisé SYMPHONIE)
était utilisé et développé par le LOB; en partenariat
avec le laboratoire Océanologique de Villefranche sur mer, l’INRIA
avait mis au point un modèle biologique de croissance algale en
conditions de double limitation par l’Azote et la lumière; la réalisation
du couplage informatique de ces deux modèles marquait l’origine
de ma mission.
Le modèle résultant du couplage des deux modèles
sus cités devait faire par la suite l’objet de développements,
afin qu’il soit susceptible de fournir des données exploitables
et appropriées à la poursuite du projet SEMPO. L’ambition
finale de mes travaux était d’isoler et de caractériser (au
regard de l’évolution de paramètres physico-chimiques) des
trajectoires de cellules de phytoplancton qui soient représentatives
de l’ensemble de celles qu’il serait possible d’observer dans un milieu
marin aux propriétés hydrodynamiques et biologiques données.
Les informations collectées seraient alors utilisées pour
réaliser des cultures de cellules de phytoplancton, dans des chémostats
reproduisant les caractéristiques physico-chimiques du milieu marin
que les particules de phytoplancton seraient susceptibles de rencontrer
en évoluant au sein de l’écosystème océanique.
I. Présentation des structures d’accueil,
du projet, et de la mission confiée
I.A/ Les structures d’accueil
Le stage que j’ai effectué s’est déroulé au sein de deux instituts de recherche: le CNRS (Centre national de la recherche scientifique), à Marseille (13) et L’INRIA (Institut National de Recherche en Informatique et en Automatique), à Sophia Antipolis (06).
I.A.1. Le Laboratoire d’Océanographie et de Biogéochimie (LOB)
Le LOB se situe principalement sur le campus de Luminy, à Marseille (13): c’est une unité du Centre d’Océanologie de Marseille (COM), CNRS-Université de la Méditerranée.
Le COM est un observatoire de l’Institut National des Sciences de l’Univers, et compte parmi les membres du réseau national des stations marines. Le COM, dirigé par monsieur Ivan Dekeyser (professeur), regroupe environ 200 personnes, réparties sur deux centres: la station marine d’Endoume, et le campus de Luminy.
Les missions du COM sont multiples: par ses recherches (en biologie, physique, chimie), il contribue au progrès de la connaissance des mers et des océans; il acquiert des données d’observation et élabore les outils théoriques nécessaires à l’analyse de ces dernières; il fournit aux communautés nationales et internationales des services liés à son activité de recherche.
I.A.2. L’Institut National de Recherche en Informatique et en Automatique (INRIA)
I.A.2.1. Situation géographique et administrative
L’INRIA est implanté dans le pôle scientifique et technologique de Sophia Antipolis (06).
Cet institut est un établissement public à caractère scientifique et technologique placé, à l’origine, sous la double tutelle du ministère de la recherche, et du ministère de l’économie, des finances et de l’industrie. L’INRIA de Sophia Antipolis, créé en 1983, est sous la présidence de monsieur Michel Cosnard, et compte 400 employés.
Ses principales missions sont décrites par le décret du 2 août 1985. Notamment, il entreprend des recherches fondamentales et appliquées en informatique et en automatique.
I.A.2.2. L’équipe COMORE
Pour ma part, j’ai eu le plaisir de travailler dans le service du projet COMORE (Contrôle et Modélisation des Ressources Renouvelables). L’objectif global de COMORE est d’appliquer et de développer des méthodes de l’automatique (modélisation, identification, estimation, régulation, contrôle optimal, théorie des jeux) et de la théorie des systèmes dynamiques aux ressources vivantes exploitées (ressources renouvelables), afin d’en améliorer la gestion. Le cadre de pensée de cette équipe est celui de l’automatique: un système, décrit par des variables d’état, est soumis à des entrées (des actions sur ce système que l’on maîtrise ou non), et est décrit par des sorties (les mesures possibles sur le système). Dans le cas de l’équipe COMORE, le système est un écosystème, modélisé par un modèle mathématique (le plus souvent à base d’équations différentielles).
Les axes de recherche principaux intéressant le projet COMORE
sont les suivants:
| . dynamique et contrôle des pêches
et de
l’aquaculture |
. modélisation de la dynamique de la
forêt
. mathématiques de la modélisation en biologie |
| . modélisation et surveillance de la
croissance du
phytoplancton |
. logiciels à usage des modélisateurs
et des
biologistes |
| . modélisation, suivi et contrôle
des procédés de
traitement de l’eau |
. modélisation et contrôle des bioréacteurs |
I.B/ Le projet SEMPO: son contexte et ses motivations
I.B.1. Le contexte du projet auquel j’ai pris part
Ce projet nommé " Action Color Hydrobio " s’inscrit dans le cadre du projet SEMPO (Simulateur d’Environnement Marin Piloté par Ordinateurs). Il est mené en partenariat par trois équipes:
I.B.2. Les motivations du projet
L’évaluation de la production primaire océanique, ou quantité de matière produite par l’activité photosynthétique des algues planctoniques est un enjeu majeur de la recherche océanographique contemporaine, fortement motivée par les problématiques liées à l’effet de serre. A l’heure actuelle, les mesures satellitaires de la quantité de chlorophylle de surface constituent l’indicateur principal de la quantité de Carbone absorbée par le phytoplancton (majoritairement sous forme de CO2), à l’échelle planétaire. Ce calcul statistique ne prend aucunement en compte les aspects liés à la dynamique des organismes phytoplanctoniques.
Il est également d’ores et déjà possible d’estimer les flux de Carbone, à plus petite échelle, selon une approche qui s’appuie sur les modèles hydrodynamiques, pour calculer la circulation dans les océans ainsi que les conditions physico-chimiques associées (température, pH, salinité,...). L’activité biologique est alors estimée à l’aide de modèles qui associent une production à des conditions d’insolation et de sels nutritifs.
Cependant, la plupart des modèles utilisés se basent sur des observations effectuées en laboratoire sur des cultures de phytoplancton monospécifiques, dans des milieux stables, c’est à dire pour une température, une intensité lumineuse et des concentrations en sels nutritifs constantes. Ces environnements ne sont donc pas représentatifs des zones de forte activité biologique, qui sont des zones hydrodynamiquement actives, et dont les caractéristiques physico-chimiques sont modifiées en permanence.
Le projet mis en œuvre s’appuie sur des modèles de simulation hydrodynamiques et biologiques (qui seront couplés), afin d’obtenir des données représentatives sur les milieux océaniques de forte production primaire (upwelling, estuaires, zones frontales,...), et sur un dispositif expérimental fortement automatisé et informatisé (cultures en chémostats), dans lequel des organismes phytoplanctoniques seront cultivés dans un environnement reproduisant les conditions de température, d’éclairement et de concentrations en sels nutritifs, proches de celles rencontrées par le phytoplancton dans le milieu marin.
A long terme, les modèles développés et utilisés
devraient contribuer à améliorer les prédictions de
la quantité de Carbone fixée durant la production primaire,
et devraient autoriser par conséquent un affinement de l’estimation
des flux de Carbone à l’interface atmosphère–océan.
I.C/ Présentation du stage et de la mission confiée
I.C.1. La mission confiée
Le LOB utilise et développe un modèle d’hydrodynamique côtière: le modèle SYMPHONIE. Ce modèle permet d’effectuer un suivi Lagrangien de particules, dans deux types d’environnement marins: le golfe du Lion, et un milieu reconstituant un upwelling académique. Ce modèle ne prend en compte que des considérations d’ordre hydrodynamique; l’activité chimique ou biologique des particules n’intervient pas.
Par ailleurs, le LOV a mis au point un modèle de croissance du
phytoplancton (paramétrisé avec l’espèce Rhodomonas
salina), en conditions de limitation simultanée par l’Azote
et la lumière. Depuis peu, ce modèle prend également
en considération la variable température (notons cependant
que cette dernière évolution n’a pas fait l’objet d’une validation
expérimentale).
. L’upwelling académique : les programmes informatiques
écrits ainsi que les résultats des simulations menées
dans ce domaine ont été le point de départ de la deuxième
phase de mon stage, visant à fournir des conclusions qui seront
nécessaires à la poursuite du projet SEMPO.
Au regard de la classification effectuée, il sera possible d’isoler des " trajectoires types " révélatrices du cheminement probable des cellules de phytoplancton au sein d’un upwelling. Les conditions (tant physiques que biologiques) du milieu rencontrées par le phytoplancton au cours de sa progression au sein de la colonne d’eau seront ensuite recréées dans des chémostats (au laboratoire d’océanographie de Villefranche sur mer). Il sera par conséquent possible d’observer en laboratoire l’activité biologique de cellules de phytoplancton évoluant dans un milieu reconstituant un cas d’upwelling.
I.C.2. L’organisation du stage
Le stage " projet de fin d’études " que j’ai effectué s’est déroulé sur une durée de cinq mois et demi, du 18/03/02 au 31/08/02, et s’est reparti de la manière suivante:
Durant cette période, mon maître de stage était Monsieur Leredde.Y, Maître de conférence sur le campus de Luminy, et chercheur en océanographie physique.
Il était primordial que je prenne connaissance, dans un premier temps des aspects hydrodynamiques du projet auquel j’allais prendre part. En outre, le modèle hydrodynamique d’environnement marin que j’allais manipuler est utilisé et développé notamment par le LOB; les enseignements et conseils de Monsieur Leredde m’ont ainsi permis de me familiariser avec ce modèle.
Ces deux mois et demi passés au LOB avaient également pour objectifs de préciser mes connaissances en hydrodynamique appliquée à l’environnement marin, ainsi qu’en informatique (langages FORTRAN, MATLAB, environnement LINUX). Cet apprentissage était basé sur l’étude d’ouvrages, et grandement favorisé par les explications de Monsieur Leredde.
Il était également fondamental que j’étudie les fondements scientifiques principaux du modèle SYMPHONIE, ainsi que son organigramme informatique, afin d’être en mesure d’apporter des modifications et petits développements à certaines sous-routines.
Par ailleurs, la présence de biologistes au sein du LOB m’a permis de préciser quelque peu mes connaissances en biologie marine, et le contact avec des statisticiens m’a permis d’aborder des notions auxquelles je devais être amené à me référer par la suite.
I.C.2.2. La période à l’INRIA de Sophia Antipolis
A l’INRIA, mon maître de stage était Monsieur Bernard.O, chercheur, chargé de recherche dans le projet COMORE.
Cette période de travail à l’INRIA avait pour but de mettre en application les enseignements qui m’avaient été dispensés et de finaliser les recherches que j’avais effectuées au LOB. Mon travail était très régulièrement orienté par les différentes personnes prenant part au projet, et notamment par Monsieur Bernard, pour toutes les questions d’ordre mathématique et informatique.
La planification du projet a nécessité la réalisation
d’un diagramme de Gantt (fourni en Annexe 1). Initialement, celui-ci ne
prévoyait que la répartition des étapes majeures de
la réalisation du projet. Tout au long du stage, j’ai rédigé
des planifications détaillées à court terme (sur des
périodes d’environ quinze jours), afin de prendre en compte les
impératifs de chacune des personnes impliquées dans le projet.
Ces planifications détaillées ont été intégrées
à la version finale du diagramme de Gantt fourni en Annexe 1.
II. Bibliographie antérieure au stage
ou préalable à la réalisation du projet
II.A/ Les domaines de simulation du modèle SYMPHONIE
II.A.1. Le golfe du Lion
II.A.1.1 Géographie et topographie de la zone

Figure II.1: Géographie et topographie du Golfe du Lion |
Le golfe du Lion est un large plateau continental (jusqu’à 70 km) localisé dans le bassin nord occidental de la Méditerranée. Limite au nord-est parle cap Croisette et au sud-ouest par le cap de Creûs, ce plateau, d’une surface d’environ 1900 km2 se présente sous une forme semi-hémisphérique et est creusé de nombreux canyons [1] qui témoignent d’importantes variations du niveau des eaux en Méditerranée [2]. La géomorphologie du golfe du Lion constitue plutôt une singularité en Méditerranée dans la mesure où cette mer, à la différence des mers épicontinentales est caractérisée par une marge continentale étroite, des bassins séparés par des seuils et dont la profondeur est comprise entre 2500 mètres et 5000 mètres [3]. |
II.A.1.2. Hydrodynamisme de la zone
Le golfe du Lion doit être considéré comme une région complexe du point de vue de l’hydrodynamique, en raison de l’interaction, à cet endroit, d’une série de phénomènes hydrologiques et atmosphériques à la fois très intenses et très variables.
Les phénomènes hydrodynamiques dans cette zone se déterminent essentiellement selon deux échelles de temps et d’espace [4]: d’abord des processus à grande échelle (plusieurs centaines de km et quasi permanents) comme la circulation générale cyclonique dirigée du nord est vers le sud ouest suivant la pente continentale, ensuite des processus à méso-échelle (de l’ordre de la centaine de km, et d’une durée variant de quelques jours à quelques mois) telle la formation d’eau dense sur le plateau continental et au large, la variation saisonnière de la stratification, ou encore les tourbillons liés aux méandres de la circulation générale.
Le phénomène atmosphérique principal est le régime des vents principalement de N-NO (Mistral, Tramontane) et dans une moindre mesure les vents de S-SE. Le forçage par le vent induit en général des processus hydrodynamiques de petite échelle dont la durée de vie n’excède pas celle du coup de vent telles les remontées côtières d’eau profonde, ou bien les ondes inertielles [4].
II.A.1.3. La production primaire dans le golfe du Lion
Les premières études menées dans le bassin nord occidental ont montré que le golfe du Lion suivait un fonctionnement biogéochimique typique d’une zone océanique tempérée [5]: l’évolution saisonnière montre un système hivernal marqué par une colonne instable et homogène sur une grande profondeur, riche en sels nutritifs et dans laquelle l’activité biologique reste réduite, puis un système printanier où la stabilisation progressive de la colonne d’eau permet le développement massif et transitoire de l’activité biologique (efflorescence phytoplanctonique, consommation des sels nutritifs) caractéristique d’un système mésotrophe. Les systèmes estival et automnal montrent une colonne d’eau stratifiée, épuisée en sels nutritifs avec un réseau trophique adapté aux conditions d’un système typiquement oligotrophe [6].
Cependant, l’évolution saisonnière décrite précédemment doit être nuancée selon les zones considérées en raison du fonctionnement hydrodynamique complexe du golfe du Lion [7].
II.A.2. Le domaine reconstituant le phénomène d’upwelling
II.A.2.1. Définition d’un upwelling côtier et processus de formation
Un upwelling côtier est un processus physique qui crée sous l’action du vent un flux vertical ascendant à la côte. Ce flux prend naissance le long du talus côtier et se dirige vers la surface. Il apporte à la côte des eaux d’origines sub-superficielles. Ces eaux sont ensuite entraînées vers le large, en dehors de la zone de remontée, par la dérive de surface. La manifestation la plus évidente d’un upwelling côtier est la formation d’un gradient de température entre la côte et le large, les eaux issues de la résurgence étant plus froides que les eaux de surface adjacentes [8].
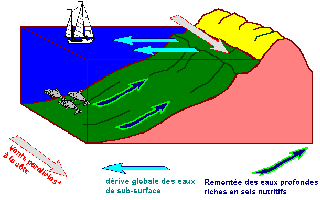
Figure II.2: schéma de formation d’un upwelling côtier
Un upwelling apporte dans la couche euphotique des éléments minéraux originaires des couches sub-superficielles. De fortes concentrations d’éléments minéraux " nouveaux " en surface sont également l’une des caractéristiques des upwellings côtiers. Cet apport d’éléments nutritifs dans la couche homogène va permettre de développer et de maintenir une forte production biologique dans la zone côtière. Ce potentiel productif est beaucoup plus important que celui existant dans les zones océaniques où la plus grande part des apports en sels minéraux provient de la régénération de la matière organique.
Un upwelling crée donc des structures physiques, chimiques et
biologiques originales qui diffèrent de celles rencontrées
habituellement dans les zones océaniques du large ou dans les écosystèmes
tempérés. Les processus qui se développent à
l’intérieur de ces structures, notamment grâce à l’apport
de sels minéraux, sont à l’origine de la forte productivité
biologique enregistrée dans les upwellings [8].
II.B/ Généralités sur les flux de matière dans l’écosystème océan
L’océan prend part au cycle global des éléments chimiques de notre planète. Il est en contact avec les autres grands réservoirs que sont l’atmosphère, la lithosphère et les couches internes du globe terrestre. Il interagit avec la biosphère continentale par l’intermédiaire de l’atmosphère et de la lithosphère.
Le schéma ci-après (Figure II.3) permet de visualiser les échanges de matière entre l’océan et les grands réservoirs terrestres.
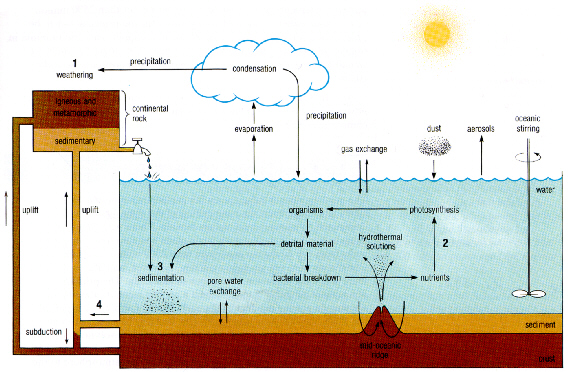
Figure II.3: Echanges de matière entre l’océan
et les grands réservoirs terrestres [ 9]
En première approximation, et sur une échelle de temps
de l’ordre de la centaine d’années, les flux de matière internes
à l’océan correspondent à un transport vertical depuis
la surface, où la matière est la plus abondante, vers les
sédiments.
Le processus de la photosynthèse permet au phytoplancton vivant dans la couche euphotique de synthétiser de la matière organique à partir des éléments présents sous forme dissoute dans l’eau de mer [10]. Une partie de cette matière reste en suspension, et une autre va être compactée par les mécanismes biologiques, tels que le broutage par le zooplancton, et par des mécanismes physiques de coagulation [11],[12],[13],[14]. Cela induit la formation d’agrégats dont la taille varie entre quelques dizaines de microns et plusieurs millimètres capables de sédimenter [15],[16]. Dans la couche euphotique, les particules en suspension et les agrégats sont recyclés plusieurs fois. Ils contribuent ainsi au maintien des écosystèmes de surface.
Une partie des agrégats quitte finalement la couche euphotique
et chute avec des vitesses allant de quelques mètres par jour à
plus de 1000 mètres par jour dans la colonne d’eau [17],[18],[19].
Lors du transfert vers les sédiments, les particules subissent encore
d’importants remaniements. Des processus physiques liés aux mouvements
des masses d’eau induisent l’agrégation et la désagrégation
des particules. Des réactions chimiques de dissolution, désorption,
d’adsorption et de précipitation interviennent également.
Les mécanismes biologiques jouent encore un rôle non négligeable
malgré la profondeur: les particules peuvent être consommées
par des organismes pélagiques et elles sont le siège d’une
activité microbienne intense [20]. Ces remaniements entraînent
la formation de particules en suspension et le transfert vers la phase
dissoute d’une partie du matériel particulaire [21]. Ce recyclage
permet d’alimenter la couche de surface en nutriments et éléments
sous forme de traces lors de remontées d’eau profonde [22].
Le schéma II.4 permet de visualiser l’origine et la distribution
des particules au sein de l’océan

Il a été mis en évidence que la variabilité temporelle des flux de particules à travers la colonne d’eau, en Méditerranée notamment, est étroitement liée au cycle annuel de la production primaire dans les eaux de surface [23].
L’activité biologique des eaux superficielles contrôle donc l’export de matière vers la colonne d’eau. Dans la majeur partie de l’océan, la disponibilité des nutriments dans la couche de surface est relativement faible et limite la production de plancton. Dans ces zones dites oligotrophes, le flux de matière est de l’ordre de quelques dizaines de mg par m2 et par jour [24]. A l’opposé, dans les zones côtières et de remontée d’eau (les upwellings notamment), les transports verticaux alimentent efficacement la couche de surface en nutriments, et la croissance du plancton n’est pas limitée. Dans ces zones eutrophes, les flux de matière peuvent être supérieurs à 1000 mg par m2 et par jour [25]. Les régions dont la productivité est intermédiaire sont qualifiés de mésotrophes.
Plus récemment, on a observé que la relation entre la
productivité des eaux de surface et l’exportation de matière
particulaire est variable, et qu’elle dépend de la composition des
communautés phytoplanctoniques [26].
Dans les régions où le flux de poussières minérales est important c’est à dire à proximité des régions arides de la planète (Afrique du nord, est asiatique et proche orient), ce dernier peut influencer significativement le cycle des particules dans la colonne d’eau [27]. En effet, la matière organique est peu dense et les agrégats sont très poreux [28]. La sédimentation des agrégats dépend donc de la présence d’exo-squelettes ou de restes de carbonate de calcium de certaines espèces planctoniques, telles que les foraminifères [17]. Par contre, les particules minérales sont également de petite taille (quelques ?m au maximum), mais elles sont denses. Elles sont incorporées dans des particules biogéniques dans la couche de surface, par collision, ou sont ingérées par des organismes filtreurs (salpes et copépodes), puis rejetées dans les pelotes fécales. De cette façon, elles augmentent la densité des agrégats, et par conséquent leur vitesse de chute. L’efficacité de ce processus augmenterait au cours de la chute des particules, au fur et à mesure du recyclage de la matière organique [29].
Les particules collectées dans la colonne d’eau sont composées
da quatre constituants majeurs. Les carbonates proviennent majoritairement
d’exo-squelettes phytoplanctoniques, tels que ceux des coccolites, et de
restes zooplanctoniques, tels que ceux des foraminifères et des
ptéropodes. L’opale (silice biogénique) provient des exo-squelettes
de diatomées ou des restes de radiolaires. Le troisième constituant
majeur est la matière organique, et le dernier correspond au matériel
terrigène. La proportion des différents constituants varie
fortement d’une région à l’autre. Dans l’océan ouvert,
la fraction biogène représente au moins 60% du flux [30].
A cause du recyclage important qu’ils subissent dans la colonne d’eau,
le flux des constituants biogènes diminue avec la profondeur [31].
II.C/ Biologie du phytoplancton
II.C.1. Généralités sur le phytoplancton utilisé pour paramétriser les modèles biologiques
Le modèle de croissance du phytoplancton utilisé au cours de ce projet a été paramétrisé avec l’espèce Rhodomonas salina, appartenant à la classe des Cryptophyceae. Cette précision n’est pas fondamentale, mais on ne peut cependant la qualifier d’anecdotique. En effet, les constantes du modèle ont été calibrées, puis optimisées, ce qui a permis de minimiser les écarts entre les sorties du modèle et les données expérimentales obtenues en chémostats, sur des cultures de l’espèce Rhodomonas salina.
II.C.1.1. Caractères généraux des Cryptophyceae
Les Cryptophyceae sont principalement des organismes unicellulaires, mobiles et pigmentés, mais il existe également des stades palmelloïdes, cocoïdes ou symbiontes et parfois des formes dépourvues de pigments (hétérotrophes). Les cellules ont une forme ovoïde et présentent un aplatissement dorso-ventral correspondant à l’insertion de deux flagelles. Ceux-ci sont de tailles équivalentes et émergent de la région vestibulaire, généralement près de la partie antérieure de la cellule. La région vestibulaire est une simple dépression de la paroi cellulaire (ou périplaste) où se vide la vacuole contractile lorsqu’elle existe. Puis la paroi s’invagine en un sillon ventral non fermé pour se terminer en un canal plus ou moins profond, le cytopharynx. Le plériplaste contient des plaques fines de nature protéique (et/ou rattachées à la membrane plasmique par des protéines) arrangées en rangs réguliers qui entourent entièrement la cellule jusqu’à la région vestibulaire. Des trichocystes de petite taille (0,1?m) sont situés à l’angle des plaques, d’autres de plus grande taille (0,5?m) bordent la région vestibulaire et le cytopharynx [32],[33].
Une caractéristique importante des Cryptophyceae est l’existence
d’un compartiment périplastidial délimité par quatre
membranes dont deux sont propres au chloroplaste, et deux appartiennent
au réticulum endoplasmique. Ce compartiment englobe le ou les deux
chloroplaste(s), plus ou moins lobé(s), le pyrénoïde,
les grains d’amidon (qui sont extra-plastidiaux) et un organite spécifique
des cryptophytes: le nucléomorphe. Le chloroplaste contient de la
chlorophylle a, de la chlorophylle c2, un seul type de phycobiline
spécifique à l’espèce, et des caroténoïdes
tels que l’alloxanthine (qui est un marqueur taxonomique des Cryptophyceae),
le ?-carot?ne, la monadoxanthine
et la crocoxanthine [34].
II.C.1.2. Rhodomonas salina
Rhodomonas salina (anciennement appelée Cryptomonas salina ou encore Chroomonas salina) présente des caractéristiques utiles à sa détermination: les plaques du périplaste sont de forme rectangulaire, les cellules possèdent un unique chloroplaste bilobé et la phycobiliprotéine présente est la phycoerythrine.
La morphologie de cette espèce semble être relativement variable. Huit formes différentes ont été recensées. Les cellules ayant fait l’objet d’études font entre 8 ?m et 16 ?m de long, 4 ?m à 8 ?m de hauteur et entre 3,5 ?m et 7 ?m de largeur [35]. Le complexe vestibule-cytopharynx est doublé avec deux rangs de 6 à 8 trichocystes. Les deux lobes du chloroplaste occupent les marges latérales des cellules. Un pyrenoïde unique est situé à la jonction des lobes et est entouré d’une couronne d’amidon.
Rhodomonas salina est une espèce très commune des eaux saumâtres et marines, présente toute l’année.
II.C.2. Activité biologique du phytoplancton
II.C.2.1. Généralités
La plupart des algues phytoplanctoniques sont des organismes unicellulaires, soit solitaires, soit organisées en groupes. Dans les cellules des eucaryotes, on distingue diverses structures dans lesquelles ont lieu les réactions anaboliques (synthèse de molécules organiques), et cataboliques (dégradation des molécules organiques).
Les structures des cellules eucaryotes intéressant principalement cet exposé sont les suivantes:
Le processus de photosynthèse se déroule en deux phases:
La production d’énergie sous forme d’ATP est assurée dans la cellule par divers processus dont le plus important et le plus efficace est la respiration. La respiration suit le processus de glycolyse, qui a lieu dans le cytosol. La glycolyse transforme une molécule de glucose en deux molécules de pyruvate en gagnant deux ATP et deux NADH (Nicotinamide Adénine dinucléotide réduit). La glycolyse peut être suivie d’un processus anaérobie: la fermentation. Il existe plusieurs types de fermentation (alcoolique, homolactique,...); toutes servent essentiellement à reconstituer le stock de NAD+, indispensable pour la glycolyse. Un autre processus peut suivre la glycolyse: la respiration, qui a lieu dans les mitochondries. Les molécules de pyruvate sont amenées dans la mitochondrie, organite dans lequel se déroulent toutes les réactions chimiques de la respiration, et sont intégrées dans le cycle de Krebs, également appelé cycle de l’acide citrique. Ce cycle permet de récupérer l’énergie du pyruvate et forme des transporteurs d’électrons comme le FADH2 (Flavine Adénine Dinucléotide réduit), NADH, et du CO2, qui est rejeté hors de la cellule.
Les transporteurs d’électrons produits lors de la glycolyse et dans le cycle de Krebs (FADH2, NADH) vont être utilisés lors de la phosphorylation oxydative. Celle-ci permet la synthèse d’ATP. Pendant le cycle de Krebs, l’énergie est emmagasinée dans NADH et FADH2; cette dernière va être utilisée pour transférer des protons H+ dans l’espace intermembranaire de la mitochondrie. Le gradient de protons ainsi créé va servir à l’ATPsynthétase pour réaliser la réaction suivante: ADP + PI ? ATP. [36]
![]()
II.C.2.4. Le métabolisme de l’Azote
L’Azote est un élément indispensable à la cellule. Il entre dans la fabrication de nombreuses molécules dont les acides aminés. L’incorporation de l’Azote dans le réseau trophique se fait par les organismes autotrophes, le plus souvent sous forme de nitrate, mais aussi sous forme de nitrite, ammoniac, ammonium d’Azote organique ou même sous forme d’Azote gazeux. L’incorporation et l’assimilation de l’Azote dans la cellule coûtent de l’énergie et nécessitent des processus particuliers. Les nitrates, une fois incorporés, sont réduits en nitrites par la nitrate réductase, lesquels sont ensuite réduits en ammonium par la nitrite réductase. L’ammonium est alors utilisé pour la fabrication des molécules organiques. [36]
II.C.3. Influence de la température, de l’intensité lumineuse, et de la concentration en Azote sur l’activité biologique du phytoplancton
II.C.3.1. Influence de la température
Globalement, on observe une augmentation de l’activité biologique du phytoplancton à mesure que la température croît, et ce jusqu’à ce que la température atteigne une valeur optimale, avant qu’une diminution rapide de l’activité ne soit constatée, provoquée par la dénaturation des molécules.
II.C.3.1.1. Répercussions sur l’activité photosynthétique du phytoplancton
La photosynthèse augmente progressivement à mesure que la température croît suivant un Q10 voisin de 2, jusqu’à ce qu’une température optimale soit atteinte (" Q " désigne le quota chlorophyllien; " Q10 = 2 " signifie que ce quota est multiplié par 2 pour toute augmentation de 10°C de la température). L’activité photosynthétique diminue ensuite rapidement [37]. Une faible température limite le transport des électrons et diminue la capacité de l’algue à utiliser l’énergie lumineuse qui se trouve en excès. Cet excès de lumière provoque une photo-inhibition, d’où la diminution de la concentration en chlorophylle a.
La réponse de la photosynthèse à haute température est affectée par la photorespiration. Etant donné que la RUBISCO fixe préférentiellement l’O2 lorsque la température est élevée, la photorespiration diminue l’efficacité de la photosynthèse. C’est pourquoi on assiste à un plafonnement de l’activité photosynthétique, puis à une chute, accélérée par la dénaturation des protéines [37].
II.C.3.1.2. Répercussions sur l’activité respiratoire du phytoplancton
L’influence de la température sur la respiration est moins traitée par la littérature. La respiration fait intervenir des processus enzymatiques dans le cycle de Krebs et des transporteurs d’électrons qui sont influencés par la température. L’activité respiratoire du phytoplancton est par conséquent liée à la température du milieu [36].
II.C.3.1.3. Répercussions sur le métabolisme de l’Azote
Le métabolisme de l’Azote est également affecté
par la température. Cette variation est certainement due à
une modification de l’activité de la nitrate réductase quand
la température varie [38]. En effet, la réduction
du nitrate en nitrite est une phase critique du métabolisme de l’Azote
[39]. Notons surtout que, dans la cellule le rapport ![]() (nommé
quota en Azote total) diminue lorsque la température croît.
(nommé
quota en Azote total) diminue lorsque la température croît.
En fait, l’activité de la nitrate réductase augmente jusqu’à une température optimale, puis diminue [38]. Une hypothèse actuellement retenue est que lorsque la température croît, l’activité de l’enzyme qui dégrade la nitrate réductase augmente. Un accroissement de la température aurait donc pour conséquence la diminution de la concentration en nitrate réductase, d’ou une baisse de l’activité de la réduction des nitrates, une fois un certain seuil de température atteint.
II.C.3.2. Influence des limitations simultanées en Azote et en intensité lumineuse sur l’activité biologique du phytoplancton
II.C.3.2.1. Présentation du processus de photoacclimatation
Une caractéristique fondamentale des organismes photosynthétiques est leur capacité à faire varier la quantité des pigments collectant la lumière en fonction de la quantité d’énergie reçue. Généralement, une pigmentation accrue se manifeste quand l’intensité de la lumière ambiante est réduite. Ce phénomène est appelé photoacclimatation.
La photoacclimatation n’implique pas de changement de la structure génétique
de la population, contrairement à la photoadaptation. La photoacclimatation
se manifeste typiquement par une réduction graduelle du contenu
en pigments photosynthétiques, en réponse à une intensité
lumineuse accrue, mais ce processus implique aussi des changements dans
les composants de la chaîne de transfert des électrons [40],
et au niveau des enzymes du cycle de Calvin-Benson [41]. Ces changements
de la composition macromoléculaire et de l’ultrastructure de l’appareil
photosynthétique caractérisent la photoacclimatation en condition
constante d’apports en nutriments [42].
II.C.3.2.1.1. Photoacclimatation en conditions saturantes en Azote
Le phénomène de photoacclimatation en conditions de saturations en N se traduit par une diminution des conditions intracellulaires en Chlorophylle a et en phycoérythrine pour des intensités lumineuses croissantes [43].
II.C.3.2.1.2. Photoacclimatation en conditions de limitation en Azote
Des mesures en chémosats ont mis évidence l’existence d’une relation non linéaire négative entre les concentrations intracellulaires en pigments et l’intensité lumineuse imposée. La limitation par la lumière induit une augmentation significative de la concentration intracellulaire en pigments. A chaque niveau d’intensité lumineuse, la concentration intracellulaire en pigments diminue avec l’intensification de la limitation par l’Azote. L’augmentation de la pente observée aux plus faibles niveaux lumineux traduit un effet moindre de la réduction de l’intensité lumineuse sur l’augmentation des pigments intracellulaires quand la croissance est limitée par l’Azote [43].
En d’autres termes, la limitation de la croissance par l’Azote réduit les capacités de la photoacclimatation.
II.C.3.2.2. Influence de la limitation en Azote sur l’absorption et l’utilisation de l’énergie lumineuse
II.C.3.2.2.1. Variations de la section efficace d’absorption
II.C.3.2.2.1.1. Définition de la section efficace d’absorption
La section efficace de l’absorption in vivo normalisée par la chlorophylle a représente la probabilité pour un photon d’être absorbé par une cellule dont le contenu en chlorophylle est connu. Comme le spectre d’absorption des algues n’est pas plat, cette probabilité dépend de la longueur d’onde du photon considéré [44].
La normalisation par la concentration en Carbone peut être perçue comme une représentation abstraite de la section efficace d’absorption par le Carbone cellulaire, l’absorption de photons par le Carbone n’ayant pas de réalité biologique [45]. La section efficace de l’absorption spécifique du Carbone renseigne sur la probabilité d’absorption d’un photon, associée à une certaine composition cellulaire.
II.C.3.2.2.1.2. La section efficace normalisée par la chlorophylle a (notée s Chla)
La section efficace d’absorption spécifique de la chlorophylle a est peu sensible au flux de photons et d’Azote. Il ressort tout de même que s Chla augmente légèrement avec l’intensité lumineuse, et s’accroît nettement lors d’une forte limitation par l’Azote (à intensité lumineuse constante). s Chla est donc sous une influence relative du taux de croissance et par conséquent, la probabilité d’absorption d’un photon par unité de pigment n’est pas strictement constante. [43]
II.C.3.2.2.1.3. La section efficace normalisée par le Carbone (notée s C)
En conditions d’Azote non limitant, la probabilité d’absorber un photon par unité de Carbone aux intensités lumineuses moyennes (IM) est significativement plus forte qu’aux intensités plus élevées (IE). Cette tendance se retrouve lorsque la croissance est limitée par l’Azote pour un flux donné de nitrates. Les valeurs de s C aux plus faibles intensités lumineuses se trouvent alors à un niveau intermédiaire, situé entre IM et IE.
La probabilité d’absorption d’un photon par unité de carbone est donc sous l’influence conjuguée de la lumière et de l’Azote. Cette probabilité est maximale aux intensités lumineuses moyennes, à saturation en Azote. Une même composition en pigments peut donc refléter des probabilités différentes d’absorption de la lumière par unité de Carbone autotrophe. [43]
Cette différence de comportement entre la section efficace spécifique de la Chlorophylle a, relativement stable, et celui de la section spécifique du Carbone, variable, provient notamment de la variabilité du rapport (Chl a) / (C), en fonction de la lumière et de l’Azote. Elle traduit la variabilité de l’efficacité de conversion de l’énergie lumineuse en production de Carbone sous l’influence des limitations simultanées par l’Azote et la lumière. Ainsi, la probabilité plus forte d’absorber un photon par unité de Carbone aux intensités lumineuses moyennes serait le reflet d’une meilleure conversion de l’énergie lumineuse en énergie chimique [43].
II.C.3.2.2.2. Rendement quantique de la production nette en Carbone
II.C.3.2.2.2.1. Définition du rendement quantique de la production nette
Le rendement quantique de la photosynthèse (noté f ) considère classiquement le rapport des photons absorbés à la masse de Carbone fixée par la photosynthèse, c’est à dire la production brute. Des données récentes ont permis de calculer le rendement quantique pour la production brute (noté f ’), qui intègre tous les processus allant de l’absorption des photons à la production de Carbone particulaire, incluant la respiration [43]. Ce rendement met en relation un flux incident de photons avec un flux sortant de Carbone organique.
II.C.3.2.2.2.2. Influence de la densité de flux de photons
Le rendement quantique de la production nette en Carbone, à l’instar du rendement quantique de la photosynthèse, suit une tendance générale de décroissance en fonction de l’intensité lumineuse incidente en conditions de saturation en Azote.
Aux intensités lumineuses moyennes, le rendement quantique est très élevé, et proche des valeurs du rendement quantique maximum pour la fixation de Carbone. Quand l’intensité lumineuse augmente, les cellules apparaissent moins efficaces, proportionnellement à la quantité d’énergie reçue. [43]
II.C.3.2.2.2.3. Influence de la limitation par l’Azote
La dispersion des valeurs de f ’ peut être attribuée à la limitation par l’Azote. En effet, pour une intensité lumineuse donnée, alors que f ’ reste stable pour une grande gamme de concentration en Azote, le rendement quantique chute pour de faibles valeurs de cette concentration [43].
La conversion de l’énergie en terme de production nette est donc
sous l’influence conjuguée de l’Azote et de la lumière.
II.D/ Quelques recherches antérieures ayant porté sur l’étude de trajectoires de cellules de phytoplancton
II.D.1. Les travaux de WOODS J.D & ONKEN R (1982) [46]
II.D.1.1. Objectifs
L’objectif principal de cette recherche était de simuler un bloom
phytoplanctonique, en partant de conditions initiales inspirées
de celles observées in situ durant les quatre saisons de l’année.
II.D.1.2. Méthode
Leurs travaux ont porté sur le couplage d’un modèle hydrodynamique à un modèle biologique, à une dimension (suivant la profondeur).
II.D.1.2.1. Les particularités du modèle
Cent " groupements " de cellules de phytoplancton étaient initialement répartis au sein de la colonne d’eau (un " regroupement" contenant un nombre de cellules déterminé). Ils étaient ensuite soumis aux influences hydrodynamiques du cadre de simulation, et faisaient l’objet d’un suivi Lagrangien.
Dans le même temps, le modèle permettait de calculer le taux de reproduction cellulaire (exclusivement influencé par la valeur de l’éclairement) de chacune des particules initialement présentes, et ainsi d’assister à l’accroissement du nombre de cellules de phytoplancton au sein de la colonne d’eau.
Cette méthode autorisait ainsi la visualisation de la répartition verticale d’un bloom phytoplanctonique.
II.D.2. Les travaux de WOLF K.U & WOODS J.D (1988) [47]
II.D.2.1. Objectifs
Ces travaux ambitionnaient, dans un premier temps, de simuler un bloom phytoplanctonique dans un milieu hydrodynamiquement peu actif, puis dans un cadre de simulation présentant les caractéristiques hydrodynamiques d’un upwelling.
II.D.2.2. Méthode
Les recherches de Wolf et Woods se sont appuyées sur les travaux de Woods et Onken (1982) [46]. En effet, le modèle utilisé est en fait un développement de celui décrit au paragraphe II.D.1. Il s’agit toujours d’une étude menée dans un environnement à une dimension (suivant la verticale).
II.D.2.2.1. Les particularités du modèle
II.D.2.2.2. Le principe des simulations
Un minimum de 20 " groupements " de cellules de phytoplancton étaient répartis tous les mètres au sein de la colonne d’eau (ceci dans un souci de cohérence avec les observations in situ).
Deux cas de figure furent alors étudiés :
Le suivi Lagrangien des " groupements " de cellules de phytoplancton permit de visualiser la répartition d’un bloom phytoplanctonique (dont l’importance était déterminée par la valeur du taux de division cellulaire, influencé par les ressources en nutriments et en énergie solaire du milieu) :
- dans un milieu hydrodynamiquement peu actif
- dans un milieu reproduisant les conditions hydrodynamiques rencontrées
dans un upwelling
III. Les modèles de simulation hydrodynamique
et biologique
III.A/ Le modèle SYMPHONIE
Le modèle utilisé est une adaptation du modèle de B.Johns, développé au département de météorologie de l’université de Reading. De nombreux développements ont été apportés depuis (effectués au Laboratoire d’Aérologie de Toulouse) et ont notamment été décrits par Estournel et al [49] et par Marsaleix et al [50]. Il s’agit d’un modèle tridimensionnel résolvant les équations de Navier Stockes en tenant compte de l’approximation de Boussinesq (variations de la masse volumique négligeable exceptées celles liées au terme de flottabilité) et de l’équilibre hydrostatique.
III.A.1. Présentation du modèle SYMPHONIE
III.A.1.1. Les équations du mouvement
Ces équations sont décrites dans un système de coordonnées cartésiennes (O,x,y,z). L’origine O se situe au niveau de repos de la surface de la mer : les axes (O,x) et (O,y) sont les axes horizontaux ; l’axe (O,z) est dirigé vers le Zénith. Dans ce repère, les équations moyennées de Navier Stockes s’écrivent:
 (3.1)
(3.1)
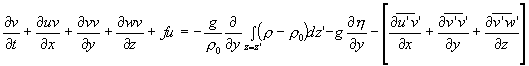 (3.2)
(3.2)
Avec:
| u,v,w: composantes de la vitesse moyenne dans le repère (O,x,y,z) | u’,v’,w’: fluctuations de ces composantes |
| f: paramètre de Coriolis | h : élévation de la surface |
| r : masse volumique de l’eau (et r o masse volumique de référence de l’eau de mer) | g: accélération de la pesanteur |
Le terme (1) est le terme de variation locale en fonction du temps, (2) et (3) sont les termes d’advection respectivement horizontale et verticale, (4) est le terme de Coriolis représentant l’influence de la rotation de la terre. Dans le second membre, (5) représente le gradient de pression lié au gradient horizontal de masse volumique et à la pente de surface. Le terme (6) représente l’influence des tensions de Reynolds (-r o . u’iv’j) sur le mouvement moyen. Dans ce dernier terme, seul le flux vertical de quantité de mouvement est retenu pour représenter la turbulence.
Ces deux équations donnent l’évolution des composantes horizontales de la vitesse de déplacement des masses d’eau.
III.A.1.2. L’équation de continuité
La composante verticale de la vitesse est déduite de l’équation de continuité en considérant
l’hypothèse d’incompressibilité : ![]() (3.3)
(3.3)
La condition cinématique qui exprime le fait que la vitesse verticale en surface est égale au déplacement de la surface s’écrit:
![]() pour z = h
(3.4)
pour z = h
(3.4)
En intégrant cette équation sur toute l’épaisseur de la couche d’eau, on obtient le déplacement de la surface de la mer (mode externe):
![]() (3.5)
(3.5)
Les composantes u et v sont les vitesses horizontales moyennes sur la verticale:
![]() avec H = h+h
: hauteur totale de la colonne d’eau (3.6)
avec H = h+h
: hauteur totale de la colonne d’eau (3.6)
Les ondes de gravité externes (h ,mode externe) sont beaucoup plus rapides que les ondes de gravité internes (champs de vitesse 3D). Elles nécessitent une résolution temporelle plus fine et conditionnent les critères de stabilité numérique du modèle. Afin d’alléger les temps de calcul, le traitement des ondes externes (Eq. 3.5) est effectué séparément selon la technique de Blumberg et Mellor [51]. Pour cela, un modèle 2D horizontal résout avec un pas de temps court comparé à celui utilisé pour résoudre les équations (3.1) et (3.2), l’équation de propagation des ondes externes (Eq. 3.5) ainsi que les équations du mouvement intégrées sur la verticale qui s’écrivent:
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
Avec ![]() et
et ![]() :
intégrations sur la verticale des termes dépendant de z dans
les équations (3.1) et (3.2).
:
intégrations sur la verticale des termes dépendant de z dans
les équations (3.1) et (3.2).
III.A.1.3. L’équation de la masse volumique
La masse volumique r est obtenue à partir de l’équation diagnostique suivante:
![]() (3.9)
(3.9)
Avec r 0=1024.8 kg.m-3, T0=13oC et S0=35. Les coefficients d’expansion thermique et de contraction saline sont respectivement donnés par a =2.41.10-4K-1 et b =7.45.10-4.
La température T et la salinité S sont déterminées de façon pronostique au moyen de leur équation de conservation respective:
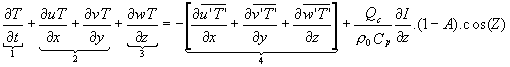 (3.10)
(3.10)
![]() (3.11)
(3.11)
Le terme (1) du premier membre est le terme de variation locale en fonction du temps et les termes (2) et (3) représentent respectivement l’advection horizontale et verticale. Dans le second membre, le terme (4) représente la contribution des flux turbulents. Qc est le flux solaire incident à la surface, (Z) est l’angle zénithal solaire, (A) l’albédo de la mer (dépendant de l’angle zénithal) et I(z) est la fraction du flux parvenant au niveau de la profondeur z.
III.A.1.4. L’équation de l’énergie cinétique de la turbulence
Les équations (3.1), (3.2),(3.10) et (3.11) comportent des termes représentant la contribution à l’évolution des paramètres moyens par les mouvements turbulents. Classiquement, les flux scalaires sont paramétrés de la manière suivante:
![]() . Dans les modèles
de méso-échelle, seuls les transferts turbulents verticaux
nécessitent d’être paramétrés. Les termes de
diffusion horizontale ne sont utilisés que pour réduire le
bruit numérique. La fermeture du problème nécessite
donc d’exprimer les coefficients de diffusion turbulente verticale c’est
à dire les viscosités turbulentes Kv et les diffusivités
turbulentes KH. Pour cela, une fermeture fondée sur l’énergie
cinétique moyenne de la turbulence (E) est utilisée:
. Dans les modèles
de méso-échelle, seuls les transferts turbulents verticaux
nécessitent d’être paramétrés. Les termes de
diffusion horizontale ne sont utilisés que pour réduire le
bruit numérique. La fermeture du problème nécessite
donc d’exprimer les coefficients de diffusion turbulente verticale c’est
à dire les viscosités turbulentes Kv et les diffusivités
turbulentes KH. Pour cela, une fermeture fondée sur l’énergie
cinétique moyenne de la turbulence (E) est utilisée:
![]() (3.12)
(3.12)
avec cK=0,1 [51]; lK est la longueur de mélange caractéristique de la dimension des tourbillons associés à l’écoulement turbulent; E est l’énergie cinétique de la turbulence calculée à partir de l’équation pronostique suivante:
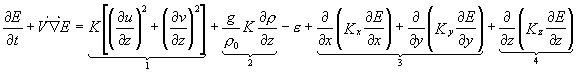
![]() (3.13)
(3.13)
Le terme (1) représente la production d’énergie cinétique de la turbulence par cisaillement de vitesse, (2) le terme de flottabilité, (3) les termes de diffusivité horizontale et (4) le terme de diffusion verticale turbulente.
e est le taux de dissipation qui est paramétré en fonction de la longueur de dissipation le :
![]() Avec ce
= 0,7 [52] (3.14)
Avec ce
= 0,7 [52] (3.14)
La paramétrisation de Bougeault et Lacarrère [53] utilisée par Gaspar et al [52] donne des longueurs de mélange et de dissipation: lK = min(lu,ld) et le = (lu.ld)1/2.
lu et ld représentent le déplacement maximal respectivement vers le haut et vers le bas que peut effectuer une particule fluide en convertissant son énergie cinétique turbulente originale en énergie potentielle; elles sont calculées à partir de l’énergie cinétique de la turbulence:
![]()
![]() (3.15)
(3.15)
Afin d’éviter des valeurs très faibles des échanges turbulents dans les couches stratifiées, une valeur minimale de l’énergie cinétique de la turbulence de 10-6m2.s-2 est prescrite [52].
III.A.1.5. L’équation de conservation
En plus des équations qui vont régir la dynamique du modèle, il faut ajouter l’équation d’un traceur qui permet de modéliser le transport dans la masse d’eau de tout élément dissous ou particulaire (et notamment biogéochimique). La concentration de ce traceur est calculée par une équation d’advection–diffusion du type:
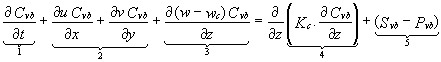 (3.16)
(3.16)
Cvb (l’indice vb désignant une variable biologique donnée) est la concentration de l’élément particulaire, wc est la vitesse de chute d’un élément particulaire; wc est nulle pour un élément dissous. Le terme (1) est la variation locale de concentration en fonction du temps, (2) est l’advection horizontale, (3) l’advection verticale à laquelle s’ajoute la chute par gravité, (4) la diffusion verticale turbulente, (5) les termes de source et de puits caractérisant l’évolution d’un élément (vb) non conservatif. Le coefficient Kc est posé égal à la diffusivité KH.
III.A.1.6. Les conditions aux limites du domaine modélisé
Je n’exposerai ici que les forçages auxquels est soumis le domaine de l’upwelling académique, lequel intéresse majoritairement mon travail.
Le modèle hydrodynamique subit deux types de forçages: les forçages aux interfaces (en surface et au fond) et les forçages aux frontières (large, côtes).
III.A.1.6.1. Les forçages aux interfaces
· En surface
Il est nécessaire de distinguer d’une part le forçage lié aux flux radiatifs de chaleur et d’autre part celui dû aux vents.
Par hypothèse, le bilan de l’énergie cinétique de la turbulence est caractérisé par un équilibre des termes de production et de dissipation. L’énergie cinétique de la turbulence dépend donc de la tension du vent et s’écrit:
![]() (3.17)
(3.17)
Les conditions aux limites pour la température et la salinité sont fondées sur la spécification des flux de chaleur et de salinité [54].
Le flux thermique à l’interface air-mer est composé du
flux de chaleur sensible (Qs), du flux de chaleur latente (Qe),
du flux radiatif infrarouge de grandes longueurs d’ondes (Qi):
il s’exprime de la manière suivante:![]()
Pour la salinité, la condition aux limites en surface est la suivante:
![]() où Prs est
la taux de précipitation pris égal à zéro dans
ce modèle, et Es est le taux d’évaporation issu
du flux de chaleur latente:
où Prs est
la taux de précipitation pris égal à zéro dans
ce modèle, et Es est le taux d’évaporation issu
du flux de chaleur latente:![]() (Lv:
chaleur latente de vaporisation).
(Lv:
chaleur latente de vaporisation).
Pour tout traceur de type variable biologique dissoute ou particulaire,
la condition limite est de gradient nul: ![]() ,
à l’interface air-mer (c’est à dire qu’il n’y pas d’échange
avec l’atmosphère).
,
à l’interface air-mer (c’est à dire qu’il n’y pas d’échange
avec l’atmosphère).
· Au fond
La tension de cisaillement du fond est paramétrée par
une relation quadratique de la vitesse d’après Blumberg et Mellor
[51]: ![]() (3.18)
(3.18)
Où Vb est la norme de la vitesse calculée sur le premier niveau de la grille à une hauteur z1 du fond, et Cd est le coefficient de rugosité. Il est relié à la longueur de rugosité du fond z0 par la relation:
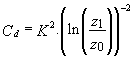 (3.19)
(3.19)
K est la constante de Von Karman définie à partir d’un profil de vitesse près du fond:
![]() avec
avec ![]() (3.20)
(3.20)
En faisant la même hypothèse que pour la surface, l’énergie cinétique de la turbulence au fond s’écrit:
![]() (3.21)
(3.21)
Les flux de chaleur et de sel sont nuls au fond: ![]() et
et ![]() en
z = -h.
en
z = -h.
Pour un élément particulaire, la condition limite à
l’interface eau-sédiment est imposée par la vitesse de sédimentation
de cet élément: ![]()
![]() (3.22) Pour un élément dissous:
(3.22) Pour un élément dissous: ![]()
III.A.1.6.2. Les forçages aux frontières latérales
? Les frontières ouvertes
Les conditions aux limites retenues au large doivent répondre à deux objectifs qui sont, d’une part d’empêcher la réflexion des ondes générées dans le domaine côtier, et d’autre part d’imposer des flux issus de l’océan hauturier. Pour répondre au second objectif, ces conditions doivent être combinées à une approche de la solution locale [55] et à un schéma de relaxation du flux [56]. Dans la modèle SYMPHONIE, ces conditions s’écrivent:
![]() (3.23)
(3.23)
Où U est la composante du transport normal à la frontière, et h l’élévation de surface libre: les termes indicés avec la notation t0 sont calculés à partir d’un forçage issu de champs à grande échelle et obtenus grâce à une méthode inverse.
Par ailleurs, un schéma de relaxation vers la circulation générale à grande échelle leur est associé pour le courant (horizontal et vertical), la masse volumique, la température et la salinité [57]. Cette relaxation s’effectue sur une zone périphérique du domaine modélisé et le temps de relaxation choisi dépend du mode (dix jours pour le mode interne et quatre heures pour le mode externe). Des conditions de type " upstream " sont ajoutées pour la masse volumique, la température et la salinité, c’est à dire que la valeur de l’océan hauturier impose la valeur à la frontière si le courant est entrant, et que la valeur à la frontière est égal à la valeur intérieure au domaine si le courant est sortant.
? Les frontières fermées à la côte
La composante du courant normale à la côte est nulle, c’est à dire qu’il n’y a aucun flux entre le continent et la mer.
III.A.1.7. Discrétisation des équations sur la grille
Sur l’horizontale, les équations primitives 3D sont discrétisées sur une grille C étagée et constituée d’un système de coordonnées cartésiennes [58].
La représentation de la topographie est facilitée par la transformation du système cartésien en un nouveau système, dans lequel la coordonnée verticale est la coordonnée double sigma. Cette coordonnée permet de diviser la colonne d’eau en deux sous domaines (figure III.1) [59]. Dans le nouveau repère, le fond sous-marin et la surface sont respectivement situés entre les coordonnées de valeur 0 et 1.
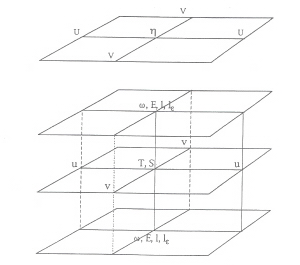
Les équations du modèle sont discrétisées sur la grille C selon la méthode des différences finies. Sur une surface sigma, les variables scalaires du modèle (température, salinité, variables biogéochimiques,...) sont définies au centre de la maille alors que les composantes horizontales (u,v) du courant sont décalées. D’autres variables comme l’énergie cinétique de la turbulence (E), la longueur de mélange (l) ou encore la composante de vitesse (w ) sont également définies au centre des mailles mais décalées d’un demi niveau vertical (niveau demi-sigma) par rapport à u, v, T et S. La taille de la maille horizontale est de 1000 mètres par 1000 mètres. L’ensemble de la colonne d’eau comprend 26 niveaux sigma verticaux.
Les schémas d’intégration numérique dans le temps et l’espace sont détaillés par Auclair [60] et Casitas [61]. La discrétisation des équations dans le temps suit notamment un schéma du type " saute mouton ": la solution au temps (t + D t) est calculée à partir des solutions aux temps (t) et (t - D t). Ce schéma a tendance à séparer les pas de temps pairs et impairs; pour cette raison, un filtre d’Asselin est utilisé. Le modèle effectue 416 itérations du mode externe pour 24 heures, soit un pas de temps de 3,5 minutes.
III.A.2. Les modifications apportées
Le modèle biologique couplé au modèle SYMPHONIE étant un modèle de croissance du phytoplancton soumis à la triple limitation Azote – Température – Eclairement, il était nécessaire que le formalisme de l’intensité lumineuse du modèle SYMPHONIE soit une approximation convenable de ce qui peut être observé in situ.
Pour cette raison, j’ai apporté quelques modifications aux modèles spatial et temporel qui étaient codés dans le modèle SYMPHONIE.
III.A.2.1 Le formalisme spatial de l’intensité lumineuse
La quantité d’énergie lumineuse pénétrant à une profondeur donnée est l’une des variables forçantes du modèle biologique couplé, car elle est à la base du processus de photosynthèse. Mais seule une partie de l’énergie lumineuse incidente est réellement disponible pour la photosynthèse. Ainsi, Morel [62], a développé un modèle qui permet de calculer à partir de l’énergie lumineuse incidente totale la quantité de lumière disponible pour la photosynthèse (le PAR). En effet, suivant la composition pigmentaire de l’appareil photosynthétique des cellules algales, seule une fraction du spectre est réellement absorbée. En outre, Morel [62] définit le rayonnement disponible pour la photosynthèse juste au dessus de la surface de l’océan, noté PAR (0+), de la manière suivante:
PAR(0+) = 43 % du rayonnement incident global (c’est à dire la fenêtre 400nm –700nm)
En traversant l’interface océan – atmosphère, une partie de ce rayonnement est réfléchi, c’est le processus d’Albedo. Ce processus compterait pour 6% en moyenne en Méditerranée. Le rayonnement incident disponible juste sous la surface, note PAR(0-), est défini comme suit:
PAR(0-) = PAR(0+) –A . PAR(0+)
Où A est le coefficient de réflexion dû au phénomène
d’Albedo. ![]()
Enfin, les propriétés absorbantes de l’eau et la présence de matière en suspension (chlorophylliennes et détritiques) induisent une atténuation du rayonnement incident avec la profondeur. L’atténuation suit, en première approximation, une loi exponentielle du type:
PAR(z) = PAR(0-). EXP(-Ks.| z| )
Où PAR(z) est l’énergie lumineuse disponible à la profondeur z, et Ks est le coefficient d’extinction de la lumière dans l’eau. Dans le cadre du domaine de simulation de l’upwelling académique, ce coefficient est calculé à la profondeur z, en fonction du contenu local en pigments ([CHL]). Notons que dans des environnements marins plus réalistes, Morel [62] préconise de tenir également compte des particules sédimentaires contribuant à accroître la turbidité de l’eau (ce qui ne sera pas considéré dans la relation proposée ici).
Ks = 0,044 + 0,0088.[CHL] + 0.054 [CHL]2/3
Ce coefficient représente l’absorption de la lumière due à l’eau pure et à la présence de pigments photosynthétiques abusivement assimilés à la chlorophylle [63].
Pour se rapporter à la variable L du modèle biologique qui était partie intégrante de mes travaux, et qui sera explicité plus bas, on utilise le facteur de conversion f.
On a ainsi: ![]()
En définitive, le formalisme spatial de l’intensité lumineuse que j’ai codé dans le modèle SYMPHONIE, est caractérisé par la relation suivante:
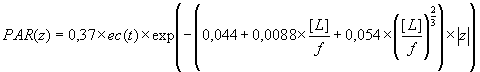
Avec: . PAR(z): Photosynthetically active radiation (?E.m-2.s-1)
. ![]() : concentration massique
en chlorophylle (mg/m3)
: concentration massique
en chlorophylle (mg/m3)
. z: profondeur (m)
Ce formalisme s’attache à reproduire les phases d’obscurité et de lumière ayant lieu au cours d’une période de 24 heures. Initialement, la valeur de l’intensité lumineuse à un instant t de la journée était fournie au modèle SYMPHONIE par la lecture d’un fichier (nommé notebook_éclairement). Cette solution a cependant du être abandonnée en raison des paliers qui étaient induits par l’attribution, discontinue dans le temps, de valeurs à l’ensoleillement,.
Il a été convenu (en s’appuyant sur les résultats d’une campagne de mesures effectuée sur l’aéroport de Nice en 1988) que la valeur maximum que j’attribuerais à l’intensité lumineuse incidente (à midi, et à la surface de la mer) serait de 2000 ?E.m-2.s-1.
Nommons ec(t) la valeur de l’éclairement, à la surface de la mer, dépendant de la variable temps (t).
Le formalisme temporel de l’intensité lumineuse, que j’ai proposé, puis codé dans le modèle SYMPHONIE, est défini par la relation suivante:
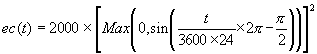
Ainsi, l’obscurité est totale entre 18 heures et 6 heures; la valeur maximale de l’intensité lumineuse incidente de surface est atteinte à midi, comme le montre le schéma ci-après (Figure III.2).
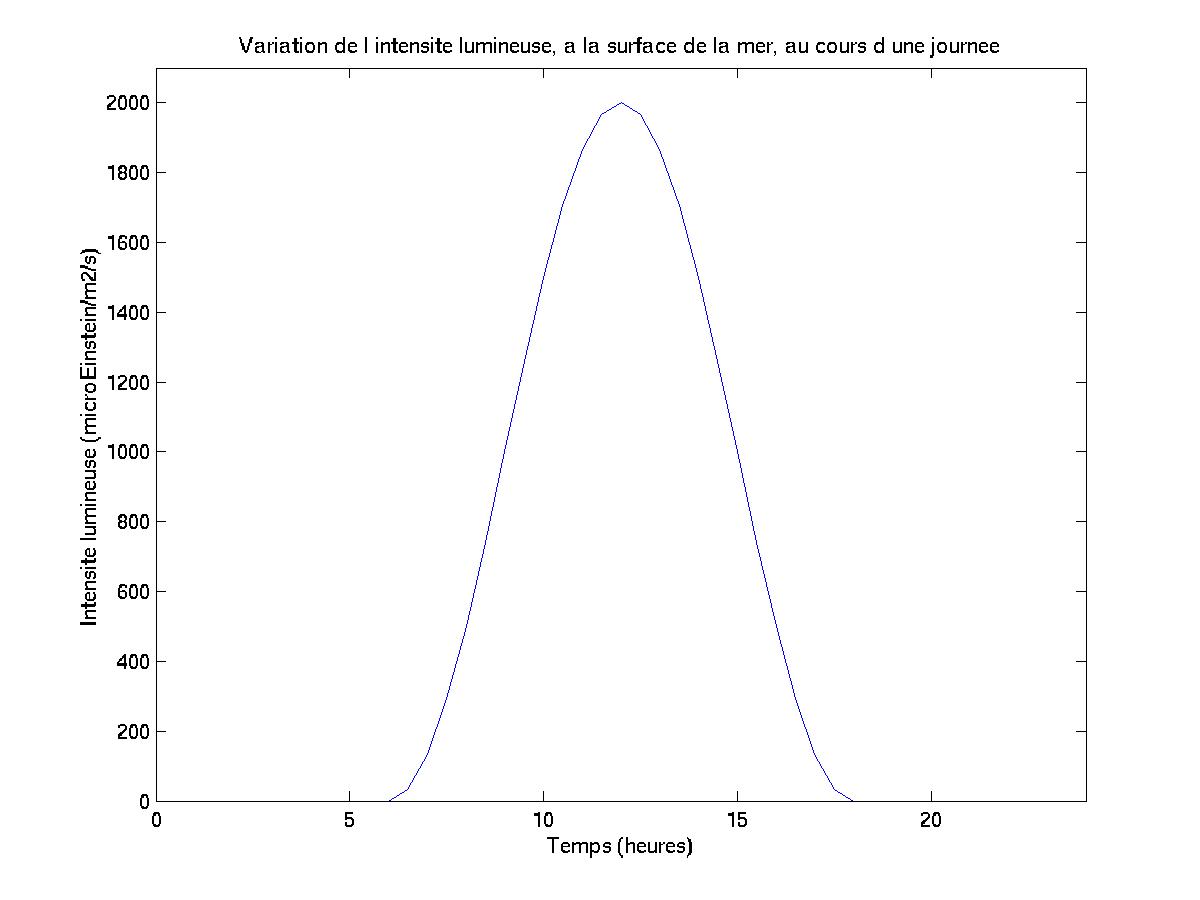
Figure III.2: Variation de l’éclairement, au cours d’une journée, à la surface de la mer
III.B/ Le modèle biologique
Le modèle biologique qui a été couplé au modèle hydrodynamique SYMPHONIE sera désigné sous le nom de modèle BioLov1 (modèle Biologique du Laboratoire Océanographique de Villefranche sur mer) pour le modèle ne prenant pas en considération le facteur limitant Température, et BioLov2, pour le modèle tenant compte du facteur limitant Température.
III.B.1. Le modèle BioLov1
Le modèle BioLov1, inspiré du modèle d’Eveillard [64], a été élaboré en 2001 par Lionel Pawlowski [65]. Les résultats fournis par ce dernier ont été confrontés à des expériences menées en chémostats, au LOV. Les chémostats utilisés pour valider ce modèle sont des systèmes ouverts: ils se remplissent et se vident en permanence, ce qui renouvelle en continu le milieu de culture et maintient la culture des micro-organismes suffisamment longtemps pour pouvoir étudier leur croissance. Les valeurs de la température (constante lors des expérimentations) et de l’intensité lumineuse étaient rigoureusement contrôlées et mesurées.
Les variables d’état ont été choisies de manière
à obtenir un modèle de faible complexité dont les
variables puissent être facilement intégrées dans un
modèle hydrodynamique. Le modèle BioLov1 est initialement
un modèle permettant de représenter la croissance du phytoplancton
(plus précisément de l’espèce Rhodomonas salina),
lorsque celui-ci est soumis à la double limitation Azote - lumière.
Le facteur limitant Température a par la suite été
pris en compte par les équations différentielles régissant
le modèle (nommé alors modèle BioLov2), selon les
résultats, et une adaptation d’une étude menée par
Cédric Pénard [66].
Le modèle BioLov1 est basé sur les hypothèses suivantes:
![]() (3.16)
(3.16)
| ? Pour le Substrat (S):
|
? Pour l’Azote particulaire chlorophyllien (L):
|
| ? Pour l’Azote particulaire non chlorophyllien
(N):
|
? Pour le Carbone particulaire:
|
j (I) et y (I) sont deux fonctions dépendant de l’intensité lumineuse (I), a’ est le taux de photosynthèse, et k’ le taux de synthèse des pigments, et sont définis de la manière suivante:
![]()
![]()
![]()
![]()
On définit également:
| ?: taux de photosynth?se
maximal (?mol C. ?mol N-1.j-1)
ki: coefficient de demi saturation (?mol quanta.m-2.s-1) kc: coefficient d’ajustement (?mol quanta.m-2.s-1) ks: coefficient de demi saturation de l’absorption (?mol N.L-1) kl: taux de synthèse maximal (j-1) I: photosynthetically active radiations (?E. m-2.s-1) |
r m:
taux d’absorption maximal
(?mol N. ?mol C-1.j-1) l : taux de respiration (j-1) b : taux de degradation des pigments (j-1) f: facteur de conversion Azote particulaire chlorophyllien-chlorophyllea (?mol N. ?gChla-1) |
La variable C représente la concentration en Azote particulaire dans le domaine de simulation. Le Carbone inorganique n’est pas représenté car il est généralement non limitant en milieu marin. Les trois autres variables sont liées à l’Azote. Le modèle considère que le nitrate externe (de concentration S) est absorbé par la cellule et se répartit en deux pools: l’Azote associé aux molécules de chlorophylle (L, dit Azote particulaire chlorophyllien) et le reste, l’Azote particulaire non chlorophyllien (noté N), la synthèse du premier se faisant à partir et au dépend du second. La somme N+L représente l’Azote particulaire total.
Une hypothèse forte de ce modèle est que le rapport de la masse d’Azote et de chromophores chlorophylliens dans une molécule de chlorophylle est constant et que, par conséquent, la variable L désigne également la concentration en chlorophylle dans le milieu, à un facteur près (que nous noterons f). Il faut souligner que N, L, et C sont des concentrations dans le milieu marin (milieu de simulation) et non des concentrations intracellulaires.
III.B.2. Le modèle BioLov2
III.B.2.1. Intérêts et bases de BioLov2
La photosynthèse, la respiration, et le métabolisme de l’Azote des cellules de Rhodomonas salina sont influencées par la température du milieu de culture. Globalement, on observe une croissance de l’activité des cellules allant avec l’augmentation de la température, jusqu’à une température d’activité optimum, suivie d’une diminution rapide de cette activité provoquée par la dénaturation des molécules. [67]
Il s’est donc avéré intéressant de considérer le facteur température dans le modèle BioLov, afin de simuler au mieux la croissance du phytoplancton au sein de l’upwelling, dans lequel les variations de la température sont précisément observables.
Le modèle BioLov2, prenant en compte la limitation de la croissance du phytoplancton par la température, a pour base deux modèles: BioLov1, ainsi que le modèle de Pénard. BioLov1 se plaçait dans une configuration où la température était constante et l’intensité lumineuse variable au cours du temps, quant au modèle de Pénard il simulait la croissance de Rhodomonas salina à intensité lumineuse constante, la température étant variable. Dans BioLov2, intensité lumineuse et température sont variables au cours du temps.
Dans le modèle de Pénard, l’influence de la température sur l’évolution de la valeur des variables du modèle de Pawlowski est prise en compte par une variable multiplicative ?(T), dont l’expression explicitée ci après est tirée de la littérature, et notamment proposée par Rosso et al [68]:
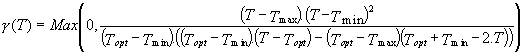 (3.24)
(3.24)
Comme nous l’avons abordé dans la partie II, il existe un processus antagoniste à la photosynthèse: la photorespiration. Ce processus augmentant avec la température, il tend à réduire la photosynthèse. On suppose par conséquent que la photosynthèse et la respiration n’évoluent pas de la même façon en fonction de la température. C’est pourquoi la température optimale de la photosynthèse est inférieure à celle de la respiration et des autres processus.
Dans l’expression de g (T), Topt est la température optimale pour l’activité respiratoire de Rhodomonas salina. Les équations du modèle BioLov2 font apparaître les fonctions g ’(T) et g ’’(T) dans lesquelles Topt est respectivement remplacée par T’opt (température optimale pour la photosynthèse) et T’’opt (température optimale pour la synthèse des pigments chlorophylliens).
III.B.2.2. Les équations du modèle BioLov2
Les évolutions des variables biologiques du modèle BioLov2
sont décrites de la manière suivante (où les termes
Svb et Pvb, (" vb " prenant le nom d’une variable
biologique donnée), sont ceux de l’équation aux dérivées
partielles (3.16) du paragraphe III.A.1.5):
| ? Pour le Substrat (S):
|
? Pour l’Azote particulaire chlorophyllien (L):
|
| ? Pour l’Azote particulaire non chlorophyllien
(N):
|
? Pour le Carbone particulaire:
|
Où S, N, L, C, ks, ki, kc, r ’m, j (I) et y (I) ont la même signification que dans le modèle BioLov1.
La méthode d’établissement de la valeur des constantes
a m, b
m, l m, r
’m et klm est détaillée au paragraphe
II.B.2.3.
III.B.2.3. Le calcul des paramètres du modèle BioLov2
Le problème majeur du modèle de Pénard réside dans le fait qu’il n’a pas pu bénéficier d’une validation expérimentale. Par conséquent, l’attribution des valeurs à certains paramètres qui le constituent résulte de l’étude de publications donnant des indications sur les valeurs de ces derniers pour une espèce proche de Rhodomonas salina: Cryptomonas ovata (qui, tout comme Rhodomonas salina appartient au genre des Cryptophyceae). Les valeurs de Tmin, Tmax, Topt et T’opt résultent de cette étude bibliographique [69].
J’ai déterminé la valeur des autres constantes de la manière suivante:
Puisque l m ,r m et b m sont des valeurs maximales, elles correspondent à la température optimale. Or, on possède les valeurs de ces paramètres pour le modèle de Pawlowski, dont l’estimation a été faite à 17° C. A priori, ces valeurs sont donc égales à celles du modèle BioLov2 pour une valeur de 17° C.
Or, puisque, d’après la formulation des équations du modèle
BioLov2, on a:
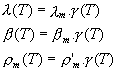 |
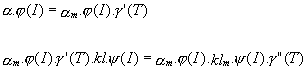 |
![]()
![]()
![]()
![]()
![]() Il
vient:
Il
vient:
Notons la différence d’attribution de la valeur des paramètres entre le modèle de Pénard et le modèle BioLov2: dans le modèle de Pénard, on affectait une nouvelle valeur aux constantes a’ et k’ de BioLov1. Dans BioLov2, l’intensité lumineuse étant variable, ce sont les valeurs de ?m et klm qui sont modifiées.
J’ai alors pu réaliser le couplage informatique du modèle
SYMPHONIE et du modèle BioLov2, étape cruciale de mon projet.
Les sorties du modèle obtenu, permettent de suivre " géographiquement
" des cellules de phytoplancton évoluant dans le cadre de simulation,
et de connaître les caractéristiques physico-chimiques ([S],
[N], [L], [C], valeurs de l’Intensité lumineuse et de la Température)
du milieu dans lequel elles se déplacent.
III.C/ Conditions initiales et variables physiques et biologiques: attribution des valeurs dans le cas de l’upwelling
III.C.1. Les valeurs initiales de la Température au sein de l’upwelling
Le cadre de simulation étant un upwelling (académique), il était nécessaire que les valeurs attribuées à la température au sein de la colonne d’eau soient en adéquation avec les mesures qui peuvent être faites lors de l’étude de ce phénomène. Les valeurs initiales que j’ai attribuées à la température au sein du domaine de simulation retranscrivent ce phénomène. Elles proviennent de relevés effectués dans le cadre du projet PROSOPE (PROductivity of PElagic Oceanic Systems), mené en partenariat par le CNRS, l’INSU et L’Ifremer. Cette campagne de mesure a été effectuée en septembre 1999 au sein de l’upwelling marocain. Notons que du fait de la saison à laquelle ces mesures ont été effectuées, l’échelle des valeurs majore probablement quelque peu celle qui aurait pu être observée au mois de mai (période de bloom que les conditions de simulation doivent reconstituer).
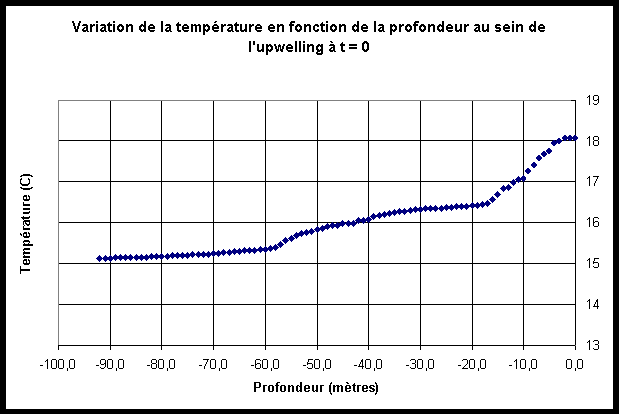 Le graphe ci-après
(figure III.3) permet de visualiser la valeur
initiale de la température en fonction de la profondeur au sein
de l’upwelling.
Le graphe ci-après
(figure III.3) permet de visualiser la valeur
initiale de la température en fonction de la profondeur au sein
de l’upwelling.
Nous observons qu’il est possible de séparer cette courbe en trois secteurs: le premier pour des profondeurs inférieures à –58 mètres, le second pour des profondeurs comprises entre –58 mètres et –18 mètres, et le troisième pour des profondeurs comprises entre –18m et 0m.
Afin de fournir au modèle SYMPHONIE des valeurs initiales de températures proches de celles de ce relevé, j’ai effectué une régression polynomiale sur les valeurs des températures de chacun de ces trois secteurs.
Les équations de régression polynomiale donnant les valeurs
de la température en fonction de la profondeur pour chacun des trois
secteurs sont les suivantes (Z est une grandeur négative qui désigne
la profondeur, en mètres, et T la température en °
C):
| Entre –92 mètres et –58 mètres
T = 0,0002 Z2 +0,0037 Z +16,866 |
Entre –58 mètres et –18 mètres
T = -0,0006 Z2 –0,0201 Z +16,232 |
Entre –18 mètres et 0 mètre
T = -0,0005 Z3 –0,0125 Z2 +18,112 |
III.C.2. Les valeurs initiales des variables biologiques des modèles BioLov1 et BioLov2 au sein de l’upwelling
Les valeurs initiales des concentrations que j’ai attribuées aux variables biologiques proviennent de données recueillies lors de la campagne MOogli 1 (Modélisation et Observation du Golfe du Lion), qui a eu lieu entre le 12/03/98 et le 16/04/98 dans le cadre du Chantier Méditerranée du PNEC. Ces dates correspondent à la période à laquelle un bloom est susceptible d’être observé en milieu marin.
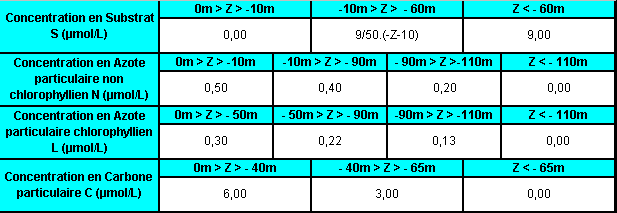
Le tableau ci-après regroupe l’ensemble des valeurs initiales des concentrations des variables biologiques intervenant dans les modèles BioLov1 et BioLov2, et qui dépendent de la profondeur à laquelle nous nous situons.
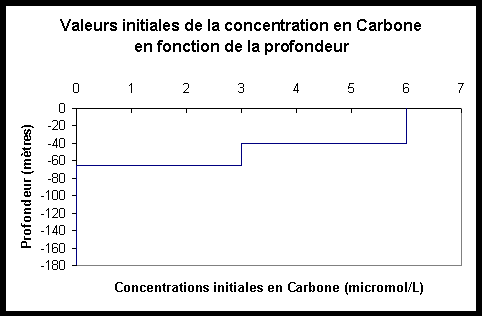
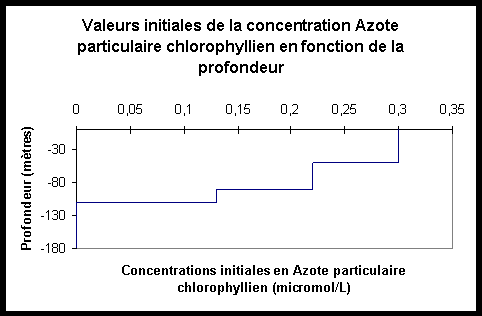 Les
graphes ci-après permettent de visualiser les valeurs initiales
des concentrations en S, N, L et C.
Les
graphes ci-après permettent de visualiser les valeurs initiales
des concentrations en S, N, L et C.
Figure III.5: Concentrations initiales en L Figure III.6: Concentrations initiales en C
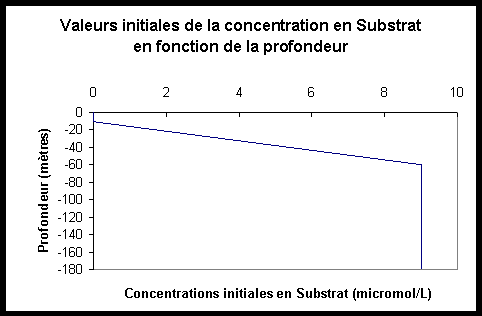
 Figure
III.7: Concentrations initiales en S Figure
III.8: Concentrations initiales en N
Figure
III.7: Concentrations initiales en S Figure
III.8: Concentrations initiales en N
Notons que, afin d’éviter la décroissance de la concentration en substrat à des profondeurs où la valeur du PAR devient nulle, il a été décidé qu’à des profondeurs telles que ?z?>65 mètres, la valeur initiale que j’attribuerais à la concentration en Carbone particulaire serait nulle. En effet, le terme de puits de l’équation différentielle régissant l’évolution de la concentration en substrat au cours du temps étant:
![]() , l’attribution de la valeur
0 à la concentration initiale en Carbone particulaire pour ?z?>65
mètres stoppera la décroissance de la concentration en Substrat
à des profondeurs inférieures à –65m (du moins tant
que le mouvement des masses d’eau n’aura pas modifié la chimiocline
du milieu).
, l’attribution de la valeur
0 à la concentration initiale en Carbone particulaire pour ?z?>65
mètres stoppera la décroissance de la concentration en Substrat
à des profondeurs inférieures à –65m (du moins tant
que le mouvement des masses d’eau n’aura pas modifié la chimiocline
du milieu).
IV. Les simulations représentatives effectuées, et les analyses et conclusions proposées
IV.A/ Le cas du Golfe du Lion
IV.A.1. But des simulations
Comme je l’ai évoqué lors de la partie I, ce cadre de simulation n’a pas été retenu pour la poursuite du projet. En effet, des conditions (physiques et biologiques) représentatives d’un cas d’upwelling ont été jugées plus faciles à reproduire en chémostats que celles d’une zone telle que le Golfe du Lion.
Cependant, les travaux menés dans le cadre du Golfe du Lion m’ont amené à écrire des routines en langage MATLAB qui permettent de visualiser les trajectoires (géographiques) horizontales de " bouées " (dont la flottabilité est considérée comme nulle) au sein de cet écosystème. Les suivis Lagrangiens obtenus pourraient être ultérieurement comparés aux trajectoires empruntées par des " bouées " (aux propriétés proches de celles considérées par le modèle SYMPHONIE) qui feraient l’objet d’un lâché en mer.
IV.A.2. Définition des simulations
Seules deux simulations seront présentées ici, chacune ayant lieu dans des zones où les influences hydrodynamiques sont de natures différentes.
IV.A.2.1. Définition de la première simulation
Quatre bouées ont été initialement placées en longitude 6 (approximativement au large de Toulon), et à 42,7 ° de latitude Nord. Leur positions initiales ne diffèrent qu’au niveau de leur profondeur:
. bouée 1: -145 mètres
. bouée 2: -70 mètres
. bouée 3: -25 mètres
. bouée 4: 0 mètre
Le suivi Lagrangien des bouées a été effectué sur une durée de 10 jours (soit 240 heures).
IV.A.2.2. Définition de la seconde simulation
Six bouées ont été initialement placées dans le grand Rhône, à proximité immédiate de la Méditerranée, selon une latitude et une longitude identiques pour chacune des bouées. Seules leurs profondeurs initiales diffèrent quelque peu: elles sont toutes situées " en surface " à des profondeurs comprises entre 0 mètre et 1,5 mètres.
De même que pour la première simulation, le suivi Lagrangien des bouées a été effectué sur une durée de 10 jours (soit 240 heures).
IV.A.3. Résultats et conclusions
IV.A.3.1. Résultats et conclusions de la première simulation
 |
Pour les bouées 1, 2 et 3 (celles situées les moins en surface), on assiste à un déplacement général vers le sud ouest, mouvement provoqué par la présence du courant Liguro-Provencal-Catalan (LPC). Ce courant transporte les eaux d’origine Atlantique avec des vitesses allant de 50 cm/s en surface à quelques cm/s à plusieurs dizaines de mètres de profondeur [57], ce qui justifie que la plus grande distance ait été parcourue par la bouée 3, celle qui est la moins en profondeur des bouées sus citées. La trajectoire de la bouée 4 (située en surface) pourrait s’expliquer par un phénomène induit par un forçage atmosphérique intervenant sur une période de temps courte, c’est à dire sur une période inertielle (d’environ 17,5 heures dans le Golfe du Lion). Des eaux stratifiées en température, |
entraînées par le vent, décrivent des mouvements anticycloniques dont le diamètre atteint quelques kilomètres pour des vitesses de l’ordre de 10 cm/s. Par ailleurs, près des côtes, ces mouvements induisent des déplacements verticaux de la thermocline qui génèrent des ondes internes se propageant vers le large à la vitesse de quelques m/s [70] (raison probable pour laquelle le déplacement de la bouée 4 se fait suivant des latitudes décroissantes).
IV.A.3.2. Résultats et conclusions de la seconde simulation
| Une première simulation (avec des positions initiales de bouées identiques à la simulation présente, mais de plus courte durée), avait montré que les bouées restaient dans le panache du Rhône approximativement pendant les 48 premières heures suivant le lâché. Durant cette période, les bouées restent en surface et décrivent un mouvement en forme de spirale, qui contribue à les éloigner progressivement de la côte. Suite à ce laps de temps, on remarque que les trajectoires de la majorité des bouée (à l’exception de la bouée 5) passent sous l’influence du courant Liguro-Provencal-Catalan; ceci s’explique par le fait que le débit moyen du Rhône ne représente environ qu’un millième du flux de la circulation générale des masses d’eau observé au large [70]. |
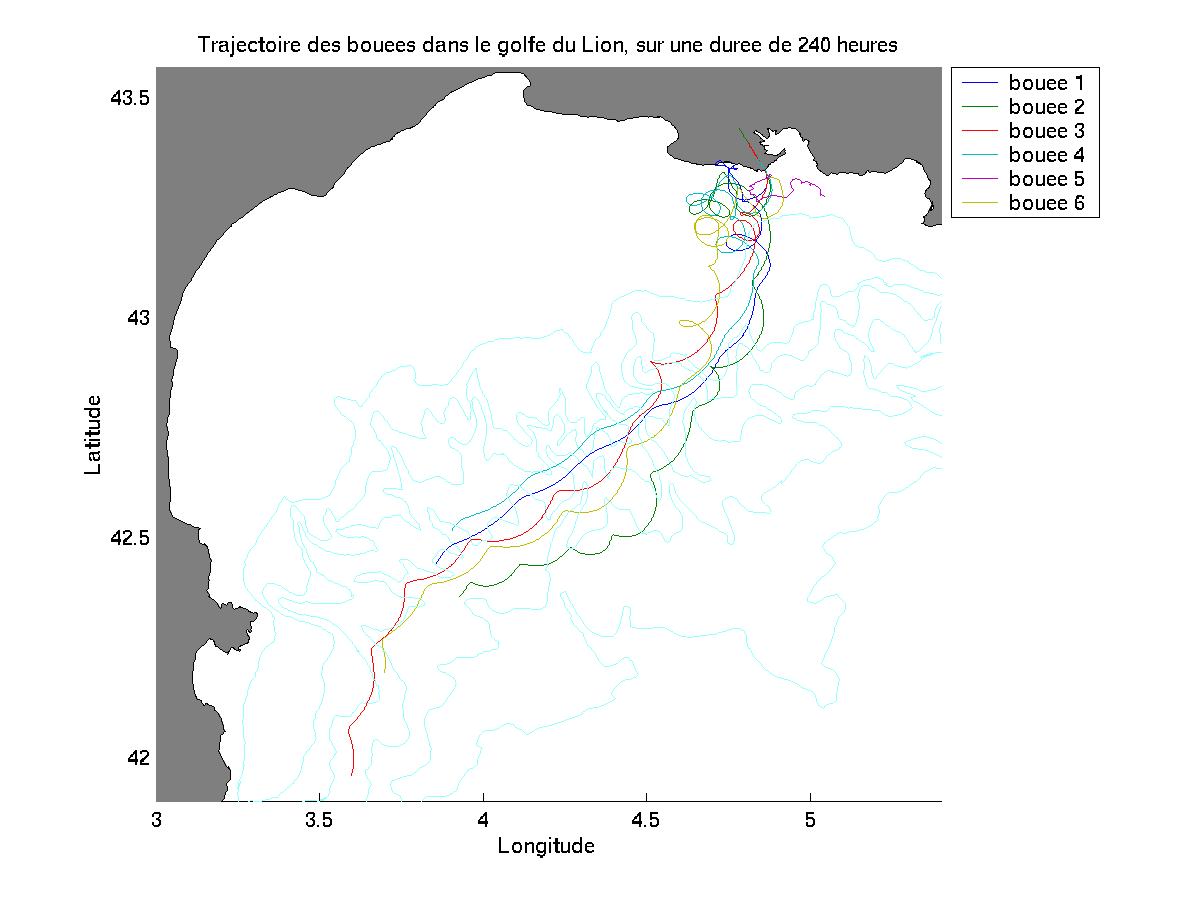 |
IV.B/ Le cas de l’Upwelling académique
Introduction
La simulation qui est présentée ici est l’aboutissement de la multitude de tests que j’ai effectuée, et qui m’a permis de déterminer les paramètres du modèle, ses conditions initiales, les grandeurs (biologiques, physiques, et mathématiques) à considérer, et les méthodes d’analyse qui seraient susceptibles de fournir les résultats les plus riches d’enseignements pour la poursuite du projet SEMPO. Les conclusions de cette étude permettront de soumettre des cellules de phytoplancton cultivées en chémostats à des conditions physico-chimiques se rapprochant de celles qu’elles seraient susceptibles de rencontrer en évoluant au sein d’un upwelling.
IV.B.1. Présentation de la simulation effectuée
IV.B.1.1. Le cadre de simulation
Le milieu de simulation est représentatif de l’hydrodynamisme rencontré au sein d’un upwelling.
IV.B.1.1.1. Ses dimensions
Le domaine, selon l’horizontale, est un carré de 100 kilomètres de côté.
Les mailles du maillage horizontal sont des carrés de 1000 mètres de côté. Certains tests ont porté sur la modification de la taille de ces mailles. La taille que j’ai finalement adoptée semble être le meilleur compromis entre précision de la définition des trajectoires calculées, et temps de calcul.
La profondeur du fond marin suit une loi de décroissance linéaire depuis la côte vers le large, la hauteur de la colonne d’eau étant de 2 mètres près de la côte et de 200 mètres à la frontière du domaine située la plus au large.
IV.B.1.1.2. Ses caractéristiques physico-chimiques initiales
Les profils verticaux initiaux de la température et des concentrations en variables biologiques ont été explicités au paragraphe III.C. Au cours de la réalisation de mon projet de fin d’études, j’ai été amené à adapter au cadre de simulation ici considéré, un programme en langage MATLAB permettant de visualiser des représentations Eulériennes de ces variables physico-chimiques.
Des représentations Eulériennes, au temps t = 0, de chacune des variables citées au paragraphe III.C sont fournies en Annexe (Annexes 2 à 5). Il s’agit de coupes verticales, perpendiculaires à la côte.
IV.B.1.2. La durée de la simulation
La durée de la simulation est de 8 jours, soit 192 heures. Une telle durée a été jugée suffisamment longue pour pouvoir observer, lors de la poursuite du projet SEMPO, l’évolution de l’activité biologique des cellules de phytoplancton qui seront cultivées dans des chémostats reconstituant les conditions physico-chimiques du milieu précédemment décrit. Le suivi Lagrangien des cellules de phytoplancton est effectué à partir du temps t = 0.
Initialement, les dimensions horizontales du domaine de simulation étaient de 50 kilomètres par 50 kilomètres. Après une durée de 96 heures, un nombre non négligeable des cellules suivies (de l’ordre de 40%), atteignaient les frontières du domaine: les données fournies par le modèle devenaient alors erronées. Pour remédier à ce problème, j’ai multiplié par deux les dimensions horizontales du domaine, et les données bathymétriques ont fait l’objet d’une interpolation linéaire de sorte à ce que la pente du fond marin du nouveau domaine soit égale à la moitié de celle du domaine initial.
IV.B.1.3. Les positions initiales des cellules de phytoplancton
La détermination des positions qu’il était convenable d’attribuer aux cellules au temps t = 0 fut une étape cruciale de la définition de la simulation finale, que je souhaitais représentative.
En effet, l’ensemble des trajectoires obtenues devait s’approcher au mieux de la totalité de celles qu’il serait possible d’observer lorsque des cellules de phytoplancton évoluent au sein d’un upwelling. Il a été constaté, au regard de l’ensemble des simulations effectuées, que les trajectoires (au sens du paragraphe I.C.1) sont grandement influencées par les positions initiales. Des trajectoires obtenues au cours de simulations tests ont fait l’objet de classifications préalables, selon la méthode qui sera explicitée en IV.B.3.1. Ces premières classifications m’ont permis de discerner et de situer certaines zones du domaine dans lesquelles les trajectoires seraient susceptibles d’être singulières. Par dichotomie, et par réitérations des nombreuses simulations menées, je pense être parvenu à isoler les positions initiales des cellules de phytoplancton, qui me permettent de réaliser une simulation représentative de la majorité des trajectoires qu’il est possible d’observer au sein de l’upwelling simulé.
Au total, 100 cellules de phytoplancton ont fait l’objet d’un suivi Lagrangien au cours de la simulation finale.
Les cellules sont repérées dans l’espace grâce à un repère orthonormé: l’axe de coordonnées i est parallèle à la côte et se confond avec la limite la plus au large du domaine; l’axe des coordonnées j est perpendiculaire à la côte et les indices j sont croissants en direction de la côte; la profondeur est définie par les coordonnées z, négatives. L’origine du repère est donc à l’interface mer-atmosphère, au large.

 Les
schémas ci-après permettent de visualiser la répartition
horizontale initiale des cellules de phytoplancton (Figure IV.3), ainsi
que leur distribution verticale initiale (Figure IV.4).
Les
schémas ci-après permettent de visualiser la répartition
horizontale initiale des cellules de phytoplancton (Figure IV.3), ainsi
que leur distribution verticale initiale (Figure IV.4).
NB: Une unité de coordonnée i ou j représente un kilomètre. Une unité de coordonnée z représente un mètre.
Les coordonnées de chacune des cellules de phytoplancton dans le repère orthonormé défini plus haut, ainsi que leur numéro d’identification sont fournis en Annexe 6.
IV.B.2. Variables étudiées et résultats
IV.B.2.1. Le choix des variables prises en considération pour établir une classification des trajectoires
IV.B.2.2.1. Aperçu de l’ensemble des trajectoires horizontales et verticales
Les suivis Lagrangiens horizontaux (Figure IV.5) et verticaux (Figure
IV.6) sont représentés par une routine que j’ai écrite
en langage MATLAB. Le but essentiel de ces graphes était de m’assurer
que la grande majorité des cellules de phytoplancton suivies ne
quittaient pas le cadre de simulation (ou du moins, pas avant un laps de
temps suffisamment long); tel est le cas. (Comme je l’ai évoqué
en IV.B.1.2, un problème de cette nature m’avait amené à
modifier la taille horizontale du domaine.)
 |
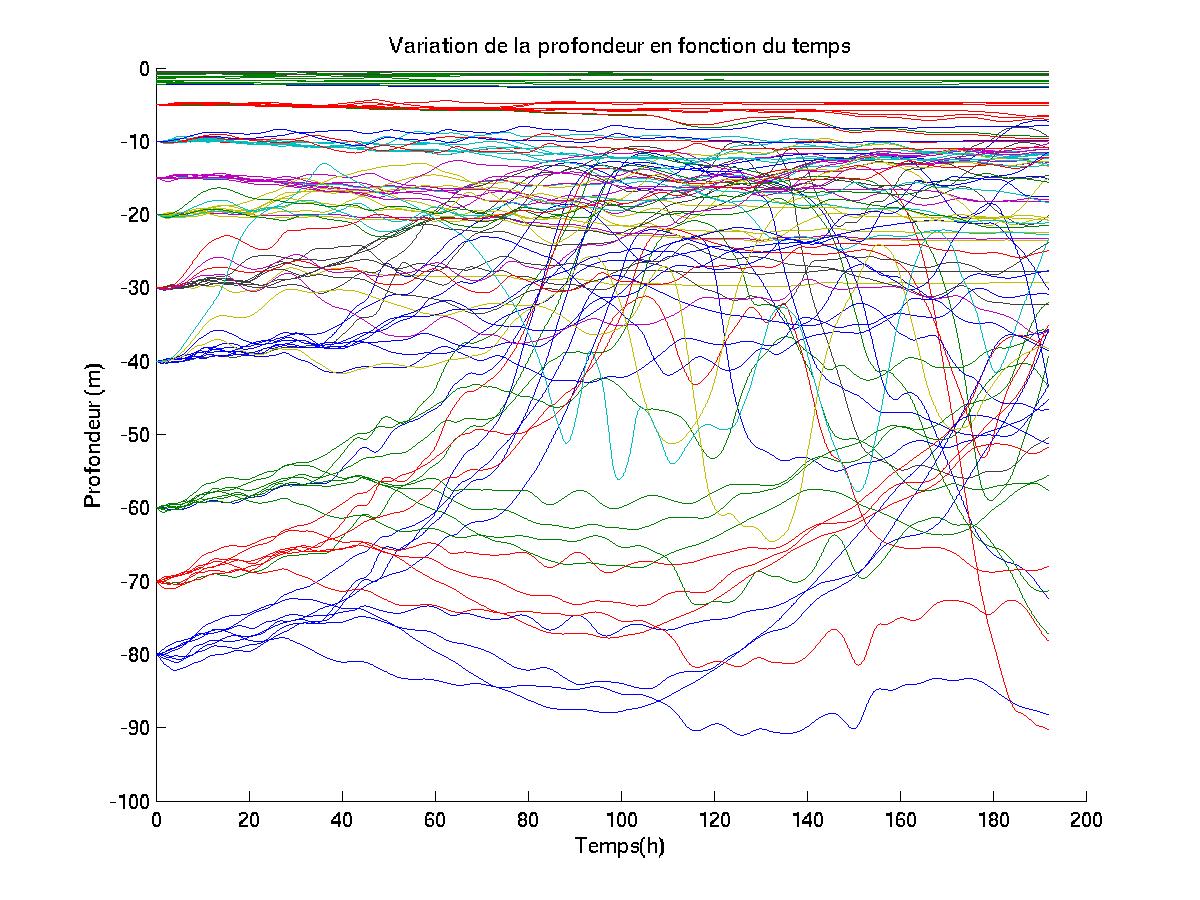 |
IV.B.2.2.2. Intérêts des suivis Lagrangiens et grandeurs retenues pour la classification: exemple
Illustrons la richesse des informations fournies par les suivis Lagrangiens des variables retenues pour établir la classification des trajectoires, en considérant le cas de la cellule de phytoplancton N° 33.
Initialement, cette cellule est située, dans le repère cartésien défini en IV.B.1.3, selon les coordonnées suivantes: (15; 25; -10).
Les figures IV.7 (suivi horizontal) et IV.8 (suivi vertical) permettent
de visualiser le déplacement géographique de la cellule de
phytoplancton tout au long des 192 heures de simulation.
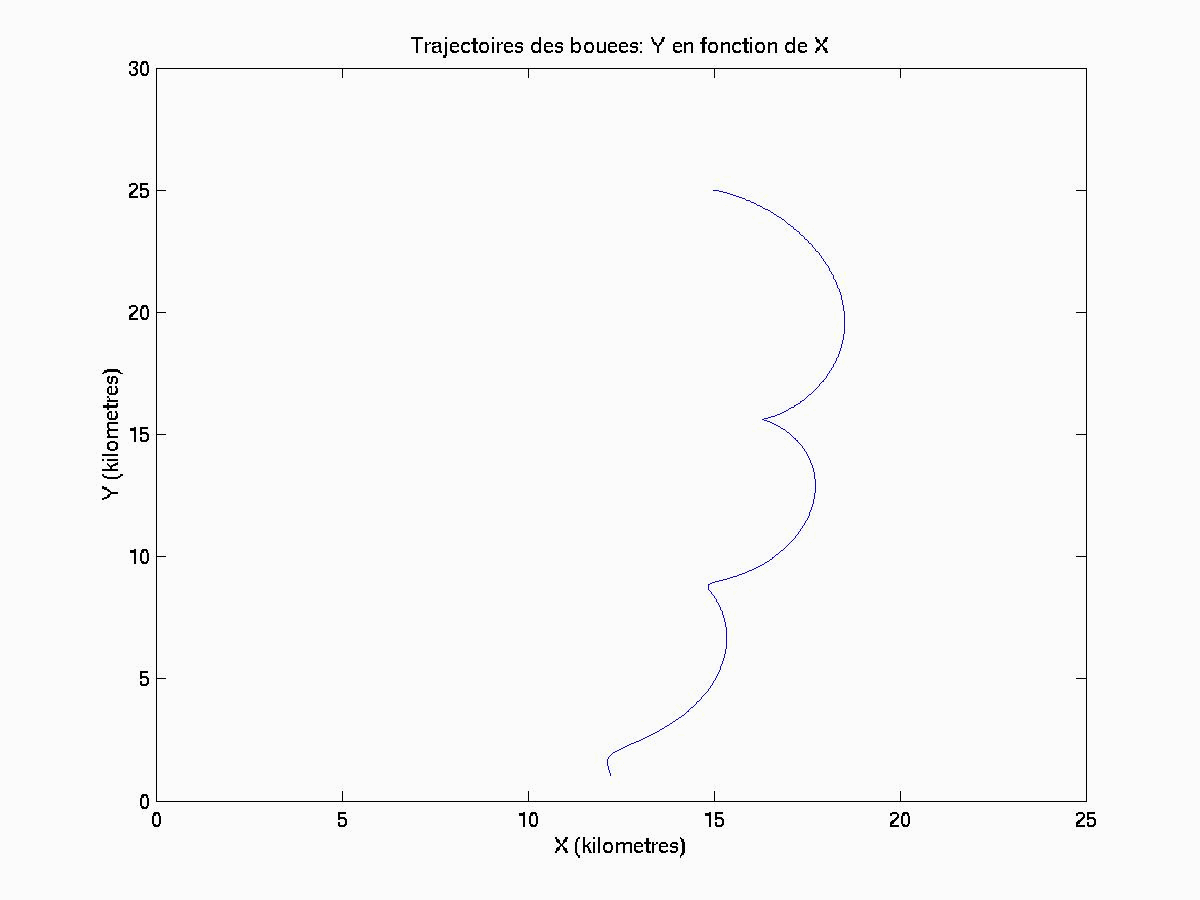 |
 |
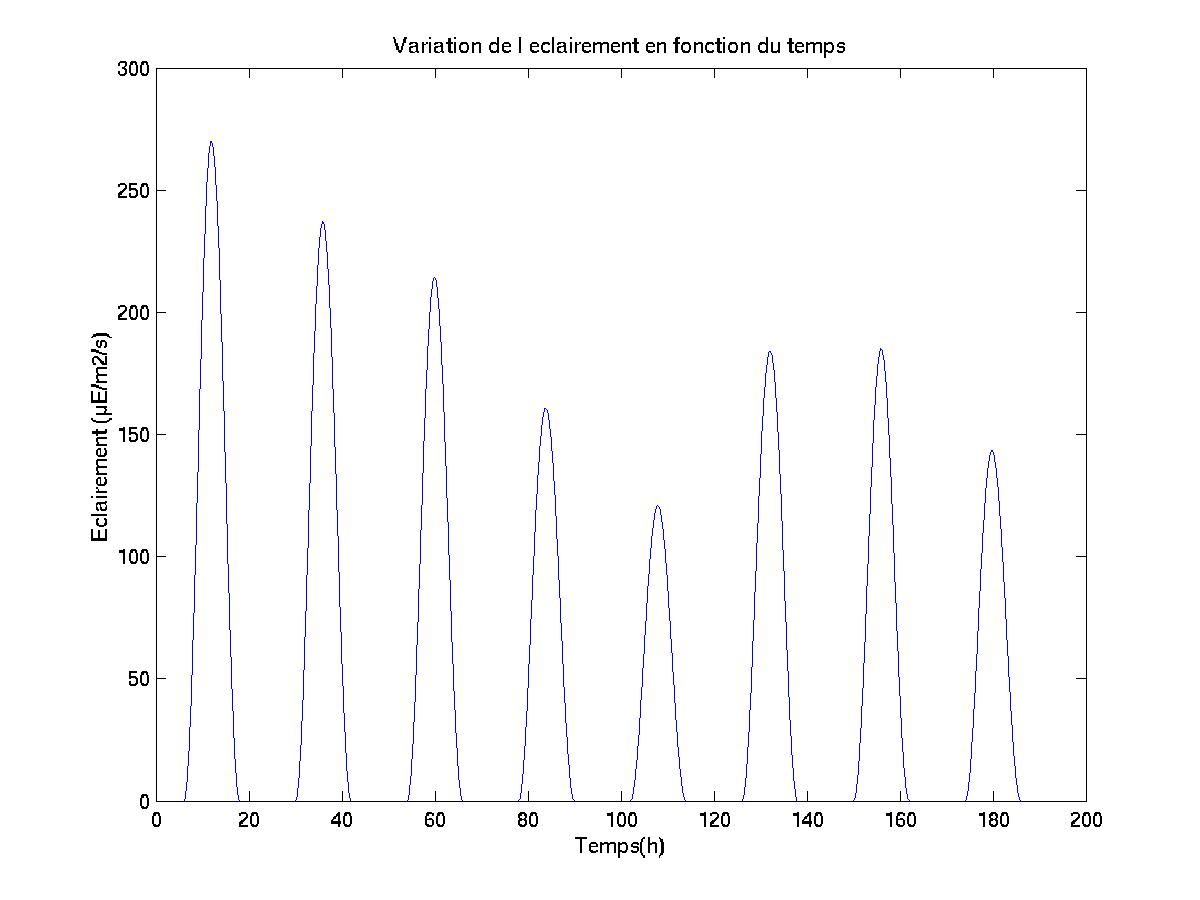 |
La structure " en pics " du graphe témoigne
de l’alternance des phases d’obscurité totale (période nocturne)
et d’ensoleillements plus ou moins intenses (périodes diurnes) auxquelles
est soumise la cellule.
La valeur des maximums est quant à elle directement reliée au positionnement vertical de la cellule. La valeur faible du pic d’intensité lumineuse au bout de 108 heures de simulation (125 ?E/m2/s) est à rapprocher de la chute de la particule de phytoplancton dans la colonne d’eau. Ainsi, en chémostats, la traduction de la variation d’un paramètre purement géographique, pourra être traduite par la modification de la valeur d’une grandeur physique. |
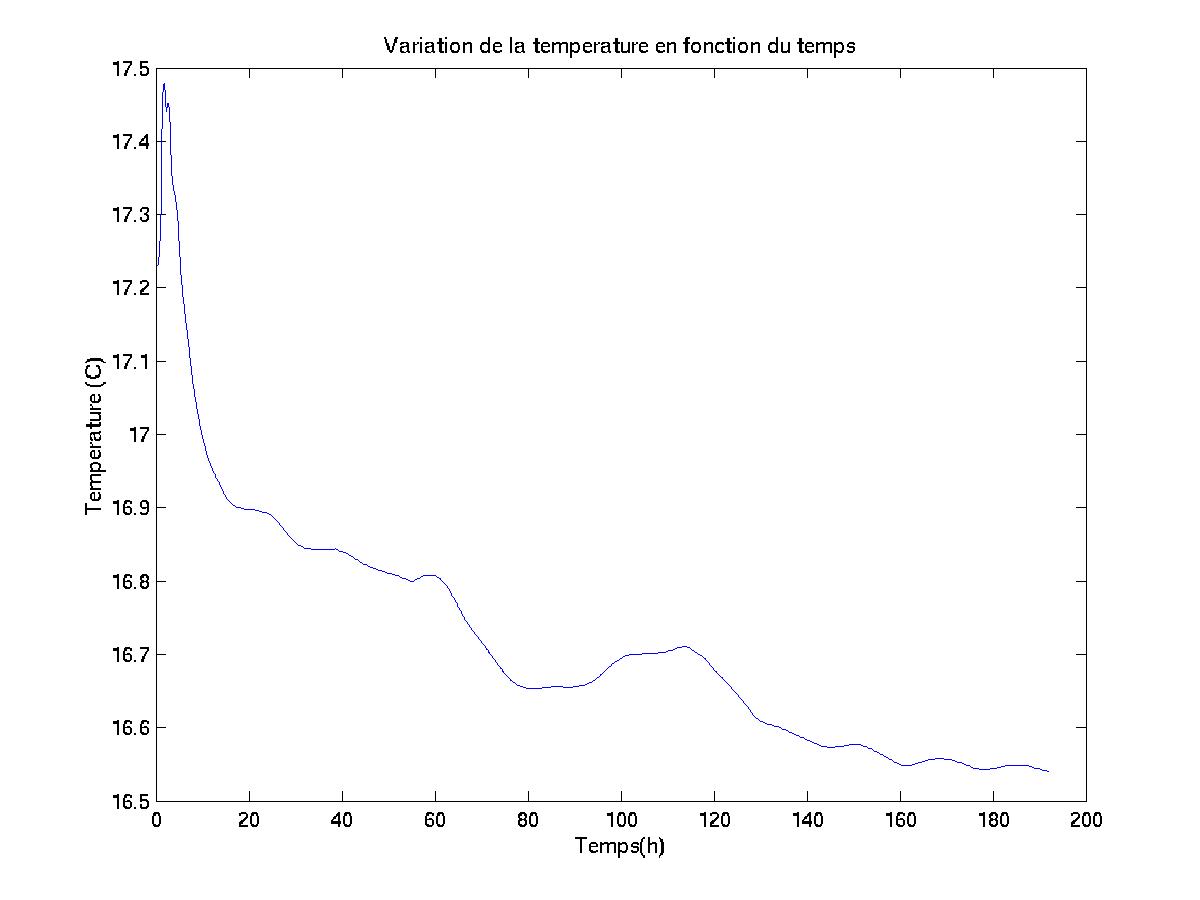 |
L’analyse comparative des graphes IV.8 et IV.10 ne suffit pas à comprendre les raisons des variations de température auxquelles est soumise la particule de phytoplancton. En effet, ce suivi Lagrangien est à rapprocher d’une représentation Eulérienne de la température (Figure IV.11) à un instant suffisamment éloigné du temps t=0 pour pouvoir visualiser l’évolution de la thermocline imposée par les phénomènes d’advection ayant lieu dans la colonne d’eau. |
 |
Il s’agit d’une coupe verticale, perpendiculaire
à la côte, au temps t = 84 heures. La figure IV.7 indique
que la cellule de phytoplancton reste située en permanence entre
des indices j compris entre 0 et 25. Aux profondeurs auxquelles évolue
la cellule (Figure IV.8), la température est voisine de 16,6°C
après 84 heures de simulation (Figure IV.11).
La prise en compte de la variable " Température " permet donc de caractériser la trajectoire des particules de phytoplancton, mais aussi de traduire l’évolution de la valeur de paramètres physiques du milieu, imposée par l’hydrodynamisme caractéristique d’un upwelling. |
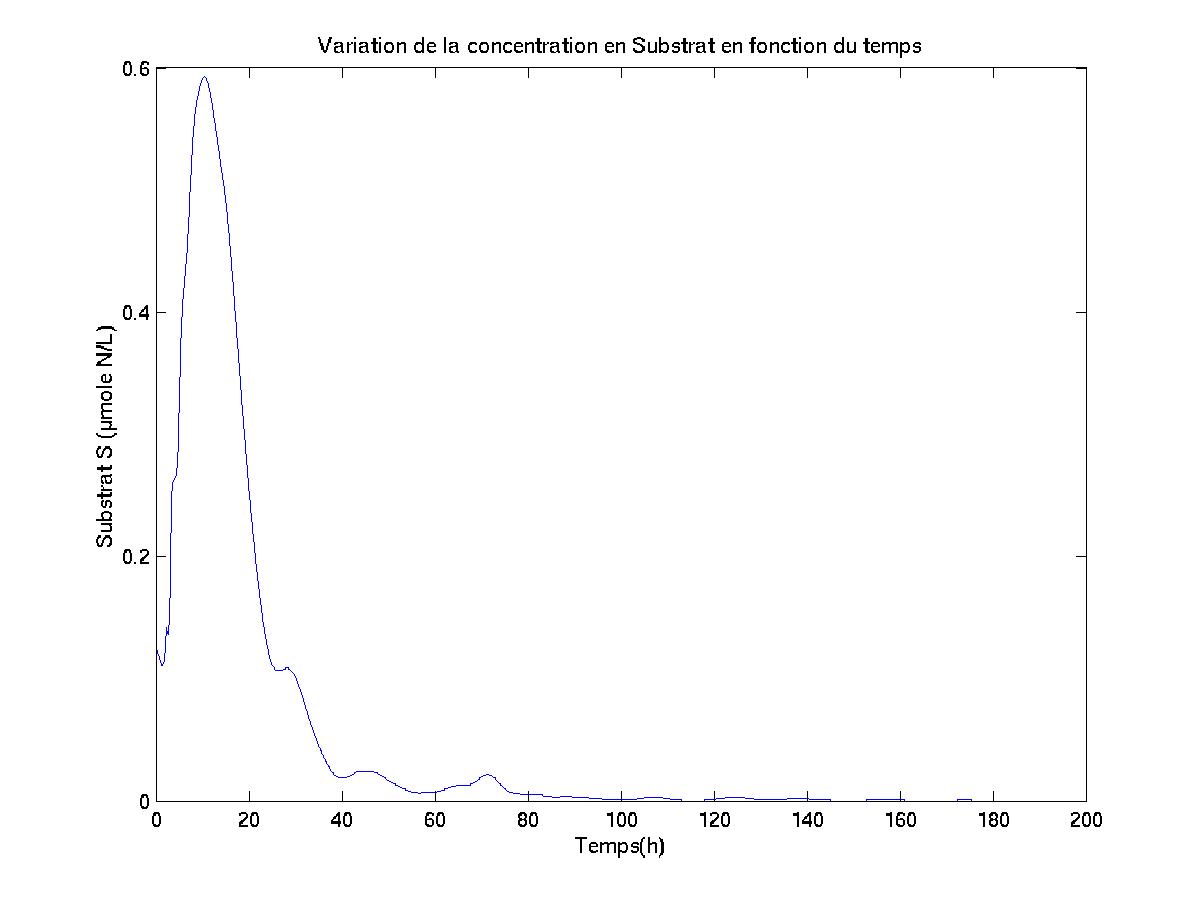 |
Dans le cas présent, la chimiocline du milieu est particulièrement observable: la cellule de phytoplancton a initialement une trajectoire ascendante (Figure IV.8) qui la place dans un niveau de la colonne d’eau où [S] a été définie comme nulle par les conditions initiales. Sa chute intervient lorsque la position de la chimiocline a été modifiée par l’activité photosynthétique du phytoplancton, et par l’hydrodynamisme du milieu de simulation: la cellule ne rencontre alors qu’une zone particulièrement pauvre en nutriments. |
Les variables choisies pour établir une classification des trajectoires se voulaient avant tout représentatives des caractéristiques du milieu rencontré par les cellules de phytoplancton. L’analyse des suivis Lagrangiens obtenus démontre que les déplacements " géographiques " des particules au sein de la colonne d’eau, ainsi que les modifications structurelles de l’upwelling, pourront être traduits (lors de la réalisation de cultures en chémostats) par l’affectation de valeurs particulières aux paramètres physico-chimiques auxquels seront soumises, in vitro, les cellules de phytoplancton.
IV.B.3. Méthodes d’analyse et de classification des trajectoires
IV.B.3.1. Méthodes d’analyse des trajectoires selon des critères quantitatifs
Les critères d’analyse " quantitatifs " s’attachent à l’évolution de la valeur des grandeurs physico-chimiques elles-mêmes. Je n’ai pas mené moi-même les calculs permettant de réaliser cette classification. Si le principe est compréhensible (et sera expliqué ici succinctement), les aspects purement théoriques sont parfois complexes, et la mise en œuvre de la méthode peut s’avérer délicate (en ce qui concerne du moins le calcul des distances orbitales). Pour ces raisons notamment, la classification proposée a été effectuée par un statisticien du LOB de Marseille (13).
IV.B.3.1.1. Première étape: réalisation d’une Analyse en Composantes Principales
L’Analyse en Composantes Principales (ACP) est une méthode d’analyse factorielle qui cherche à réduire un nombre important d’informations (prenant la forme de valeurs sur des variables) à quelques grandes dimensions. Comme dans toute analyse statistique, on tente donc d’expliquer la plus forte proportion de la variance par un nombre aussi restreint que possible de variables (les composantes). On utilise le terme de variables latentes pour parler de ces variables qui existent au plan conceptuel seul et qui ne sont pas mesurées.
L’ACP cherche une solution à l’ensemble de la variance des variables mesurées. De plus, elle cherche une solution où les composantes sont orthogonales entre elles (c’est à dire indépendantes). Il s’agit d’une méthode factorielle car la réduction du nombre des caractères ne se fait pas par une simple sélection de certains d’entre eux, mais par la construction de nouveaux caractères synthétiques obtenus en combinant les caractères initiaux au moyen de " facteurs "; c’est une méthode linéaire car il s’agit de combinaisons linéaires. [71]
La première étape de la classification des trajectoires
selon des caractères quantitatifs a consisté à réaliser
une ACP sur les trois variables suivantes: Concentration en Substrat, Intensité
lumineuse, et Température.
IV.B.3.1.2. Le calcul des distances orbitales
Le calcul des distances orbitales consiste à déterminer la distance minimum séparant les courbes caractéristiques de chacune des cellules de phytoplancton (définies par les coordonnées factorielles de l’ACP effectuée au préalable), en translatant chacune de ces courbes les unes par rapport aux autres. Ainsi, une matrice d’interdistances orbitales entre les cellules de phytoplancton a été calculée. L’avantage du calcul d’une distance orbitale, comparativement à celui d’une distance Euclidienne, réside dans le fait qu’il permet de détecter les similitudes entre les allures de deux courbes, même si les variations " analogues " se produisent avec un décalage temporel.
IV.B.3.1.3. Détermination des classes de cellules phytoplanctoniques
En dernier lieu, une ACP a été réalisée sur les valeurs de la matrice d’interdistances orbitales. Des représentations graphiques dans les trois premiers plans factoriels ont alors été tracées et ont permis de détecter les cellules qui semblaient être regroupées dans ces plans, et ainsi de constituer des classes de trajectoires.
IV.B.3.2. Méthodes d’analyse des trajectoires selon des critères qualitatifs
Les critères d’analyse qualifiés de " qualitatifs " s’intéressent en fait à des grandeurs mathématiques caractéristiques des courbes donnant l’évolution d’une variable donnée au cours du temps. Pour chacune des variables retenues pour établir une classification (définies en IV.B.2), la courbure, ainsi que le nombre d’extremums principaux des graphes " (Variable) = f (temps) ", ont été calculés à l’aide de programmes que j’ai rédigés, en langage MATLAB.
IV.B.3.2.1. Calcul du rayon de courbure
Considérons une fonction du type: V = f (t).
l’éclairement, soit la température)
. t désigne le temps
? Si l’on considère f comme une fonction paramétrée
en t, les coordonnées ![]() d’un
point de (C) sont données à tout instant par le système
d’équations:
d’un
point de (C) sont données à tout instant par le système
d’équations:
![]()
? Les coordonnées ![]() d’un
point de (C’) seront données par le système d’équations
:
d’un
point de (C’) seront données par le système d’équations
:
![]() où V’ est la valeur
de la dérivée première de la fonction f en t.
où V’ est la valeur
de la dérivée première de la fonction f en t.
? Les coordonnées ![]() d’un
point de (C") seront données par le système d’équations
:
d’un
point de (C") seront données par le système d’équations
:
![]() où V" est la valeur
de la dérivée seconde de la fonction f en t.
où V" est la valeur
de la dérivée seconde de la fonction f en t.
? Par définition, la courbure (notée ?), en t, de la courbe (C) est fournie par la relation:
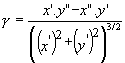 et par suite, il vient:
et par suite, il vient: 
? Pour chacune des variables étudiées, et pour chacune des 100 cellules de phytoplancton, la valeur de ? a été calculée toutes les deux heures. Ce calcul a été effectué par des programmes que j’ai rédigés, en langage MATLAB (le programme permettant de calculer la courbure des graphes [S] = f (t) est fourni en Annexe 7).
IV.B.3.2.2. Calcul du nombre d’extremums principaux
IV.B.3.2.2.1. Principe du calcul
Comme au paragraphe précédent, considérons une
fonction du type V = f (t), et (C) sa courbe représentative.
? La présence d’un extremum local sera caractérisée par l’annulation de la dérivée première de la fonction f. C’est cette propriété qui est utilisée par le programme MATLAB que j’ai écrit pour déterminer le nombre total d’extremums d’un graphe donné. Ce programme (composé d’une routine principale et d’une sous-routine) est fourni en Annexe 8.
? Cependant, j’ai considéré que certains extremums locaux n’étaient pas à prendre en compte dans ce dénombrement. En effet, localement, des annulations successives rapides de la dérivée première peuvent traduire la présence de " bruit ", notamment, sans pour autant être représentatifs de l’allure globale de la trajectoire. Pour cette raison, il était nécessaire de définir des critères qui puissent caractériser ces extremums. Deux critères ont été retenus.
. la catégorie des extremums séparés par une durée supérieure à 10 heures
IV.B.3.2.2.2. Exemple
Illustrons le calcul expliqué au paragraphe précédent
par un exemple simple. Pour cela, considérons le graphe : [Substrat]
= f(temps) de la cellule de phytoplancton n°2 (Figure IV.13). Cette
trajectoire (l’utilisation de ce terme a été justifiée
au paragraphe I.C.1.) a été choisie pour illustrer la démarche
mise en œuvre, dans la mesure où elle présente des variations
facilement observables.
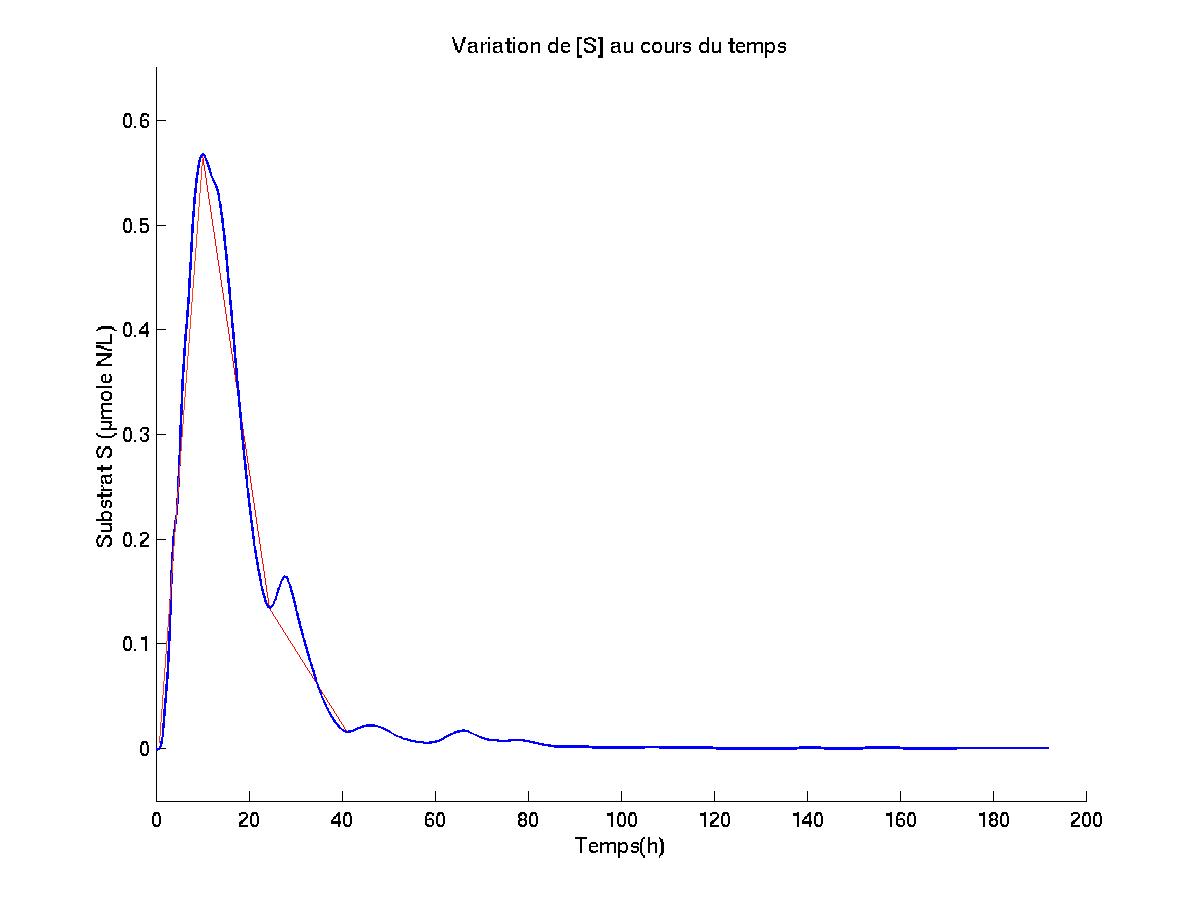 |
Le programme MATLAB dénombre
4 maximums principaux (reliés ici entre eux par 3 droites de couleur
rouge). Nous constatons ainsi que ce programme a permis de " filtrer "
notamment les extremums observés pour un temps supérieur
à 40 heures, qui, rapportés à l’échelle de
valeurs des concentrations sont peu significatifs; en effet, des variations
de la concentration en Substrat de si faibles amplitudes ne témoignent
pas de modifications conséquentes de la trajectoire de la cellule
dans la colonne d’eau.
Ce même programme indique, que 3 extremums sont séparés par des durées supérieures à 10 heures (les 3 derniers), le premier étant séparé du second de 9 heures et 40 minutes. |
L’écriture d’un tel programme m’a permis de traiter un nombre considérable de données. En effet, trois types de graphes ont été étudiés ([Substrat] = f(t), Eclairement = f(t), et Température = f(t)), pour chacune des cent cellules de phytoplancton suivies, chaque graphe étant défini par 3188 valeurs.
IV.B.3.2.3. Détermination des classes de cellules phytoplanctoniques
IV.B.3.2.3.1. Le cas du critère " Nombre d’extremums principaux "
Chaque cellule de phytoplancton est caractérisée par trois séries de valeurs (une série pour chacune des variables étudiées), chaque série contenant trois valeurs (explicitées en IV.B.3.2.2.1). La première étape a consisté à réaliser une ACP sur les valeurs sus mentionnées, après avoir supprimé, pour chaque série propre à chaque cellule, la donnée relative au nombre total d’extremums principaux, cette valeur étant égale à la somme des deux autres.
La détermination des classes a ensuite été rendue possible au regard de représentations graphiques effectuées dans les quatre premiers plans factoriels.
IV.B.3.2.3.2. Le cas du critère " Valeurs de la courbure "
Ces valeurs n’ont pas fait l’objet de calculs permettant de proposer une classification des trajectoires de phytoplancton. Le calcul des distances orbitales entre valeurs caractérisant chacune des cellules pourrait constituer une voie de réflexion. Cependant la problématique soulevée pourrait être plus complexe qu’il n’y parait, car il s’agit de données quantitatives, caractéristiques d’une grandeur mathématique (la courbure) constituant donc des renseignements d’ordre qualitatif sur les trajectoires des cellules de phytoplancton.
Les valeurs des courbures des trajectoires des 100 cellules, concernant
chacune des trois variables étudiées, seront fournies aux
chercheurs du LOV. Les données obtenues suite à mes calculs
pourraient ainsi faire l’objet de travaux ultérieurs.
IV.B.4. Résultats de la classification des trajectoires des cellules phytoplanctoniques
IV.B.4.1. Classification des trajectoires selon des critères d’ordre quantitatif
IV.B.4.1.1. Les classes déterminées
La méthode décrite en IV.B.3.1 a permis de séparer l’ensemble des 100 trajectoires de cellules de phytoplancton en quatre classes de trajectoires distinctes.
Le tableau ci-après (Tableau IV.14) indique la composition de chacune de ces classes.
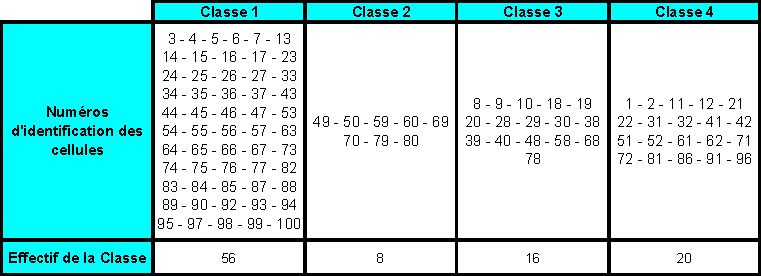
IV.B.4.1.2. Détermination des caractéristiques physico-chimiques représentatives de chacune des classes
Cette classification signifie qu’au sein d’une même classe, les cellules de phytoplancton ont été soumises, d’un point de vue quantitatif, à des conditions physico-chimiques comparables (en ce qui concerne la concentration en Substrat, l’intensité lumineuse, et la Température).
Pour chacune de ces classes, j’ai déterminé la cellule de phytoplancton qui se situe la plus proche du centre de gravité de la classe à laquelle elle appartient, ce que l’on nomme en statistique le parangon. Cette cellule peut être considérée comme la plus représentative de sa classe.
Les parangons de chacune des classes sont le suivants:
| - Classe 1: cellule 56 | - Classe 2: cellule 59 | - Classe 3: cellule 58 | - Classe 4: cellule 1 |
Les évolutions de la concentration en Substrat, de l’Intensité
lumineuse, et de la Température au cours du temps auxquelles ont
été soumis les parangons de chacune des 4 classes peuvent
être visualisés sous forme de graphiques fournis dans les
Annexes 9 à 12; les fichiers de valeurs (chaque graphe étant
défini par 3188 valeurs) seront par ailleurs transmis aux chercheurs
du LOV.
IV.B.4.2. Classification des trajectoires selon des critères d’ordre qualitatif (nombre d’extremums principaux)
Pour les raisons évoquées en IV.B.3.2.3.2, seuls les résultats d’une classification basée sur le nombre d’extremums principaux sont exposés dans ce paragraphe.
IV.B.4.2.1. Les classes déterminées
De même que dans le cas de la détermination de classes de trajectoires selon des critères d’ordre quantitatif, quatre classes ont pu être isolées suite à la mise en œuvre de la méthode décrite aux paragraphes IV.B.3.2.2 et IV.B.3.2.3.1.
Le tableau ci-après (Tableau IV.15) indique la composition de chacune de ces classes. Les noms des classes sont tout à fait arbitraire.
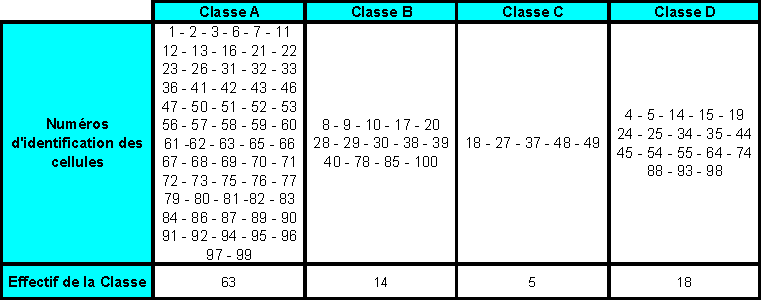
IV.B.4.2.2. Détermination des caractéristiques physico-chimiques représentatives de chacune des classes
J’ai déterminé le parangon de chacune de ces 4 classes. Pour une classe donnée, le cellule définie est la plus représentative, au sein de sa classe, du nombre de variations, et de leurs types, des caractéristiques physico-chimiques auxquelles elle a été soumise en évoluant dans la colonne d’eau. Ainsi, selon ces critères de classification, il est envisageable que des cellules ayant été soumises à des concentrations en Substrat, à des intensités lumineuses, ou à des températures, situées sur des échelles de valeurs très différentes, soient regroupées dans la même classe.
Les parangons de chacune des classes sont le suivants:
| Classe A: cellule 36 | - Classe B: cellule 28 | - Classe C: cellule 37 | - Classe D: cellule 19 |
Les évolutions de la concentration en Substrat, de l’Intensité
lumineuse, et de la Température, au cours du temps, auxquelles ont
été soumis les parangons des classes B, C et D peuvent être
visualisés sous forme de graphiques fournis dans les Annexes 13
à 15; les fichiers de valeurs seront par ailleurs transmis aux chercheurs
du LOV.
V. Analyses comparatives, perspectives, limites des méthodes mises en oeuvre et des résultats obtenus
V.A/ Significations et analyses comparatives des classifications proposées
V.A.1. Significations des classifications proposées
Deux méthodes de classifications m’ont permis de déterminer, chacune, quatre classes de trajectoires.
Cela signifie que l’ensemble des conditions physico-chimiques rencontrées par des cellules de phytoplancton évoluant au sein d’un upwelling durant 192 heures, peuvent être reproduites en chémostats, au regard de deux classifications s’appuyant sur deux critères de natures différentes, et dont la signification est par conséquent différente:
Au regard des résultats, nous pouvons noter quelques similitudes entre les classes définies pour les unes par la méthode CQT et pour les autres par la méthode CQL:
· Tout d’abord, les deux types de classification ont permis de séparer les 100 cellules de phytoplancton en un nombre identique de classes (quatre).
· Les effectifs des classes (c’est à dire le nombre de cellules qu’elles regroupent) ont des valeurs comparables deux à deux.
Ainsi, chacune des méthodes a permis de constituer une classe regroupant près de 60 % des cellules ayant fait l’objet de suivis Lagrangiens, une classe dont l’effectif est faible (inférieur à 10 % des cellules étudiées), et deux classes aux effectifs similaires (de l’ordre de 20 % des cellules suivies).
· Intéressons-nous à la composition de ces classes.
Il apparaît que la classe 1 (classe issue de la méthode CQT dont l’effectif est le plus important) possède 60,7 % de cellules en commun avec la classe A (classe issue de la méthode CQL dont l’effectif est également le plus élevé). Autrement présenté, 34 cellules de la classe 1 appartiennent également à la classe A.
Ces deux similitudes notables m’ont amené à comparer les trajectoires (en terme de concentration en Substrat, d’Eclairement et de Température) des parangons de ces deux classes. Les graphes ci-après (Figure V.1) permettent d’effectuer visuellement cette comparaison.
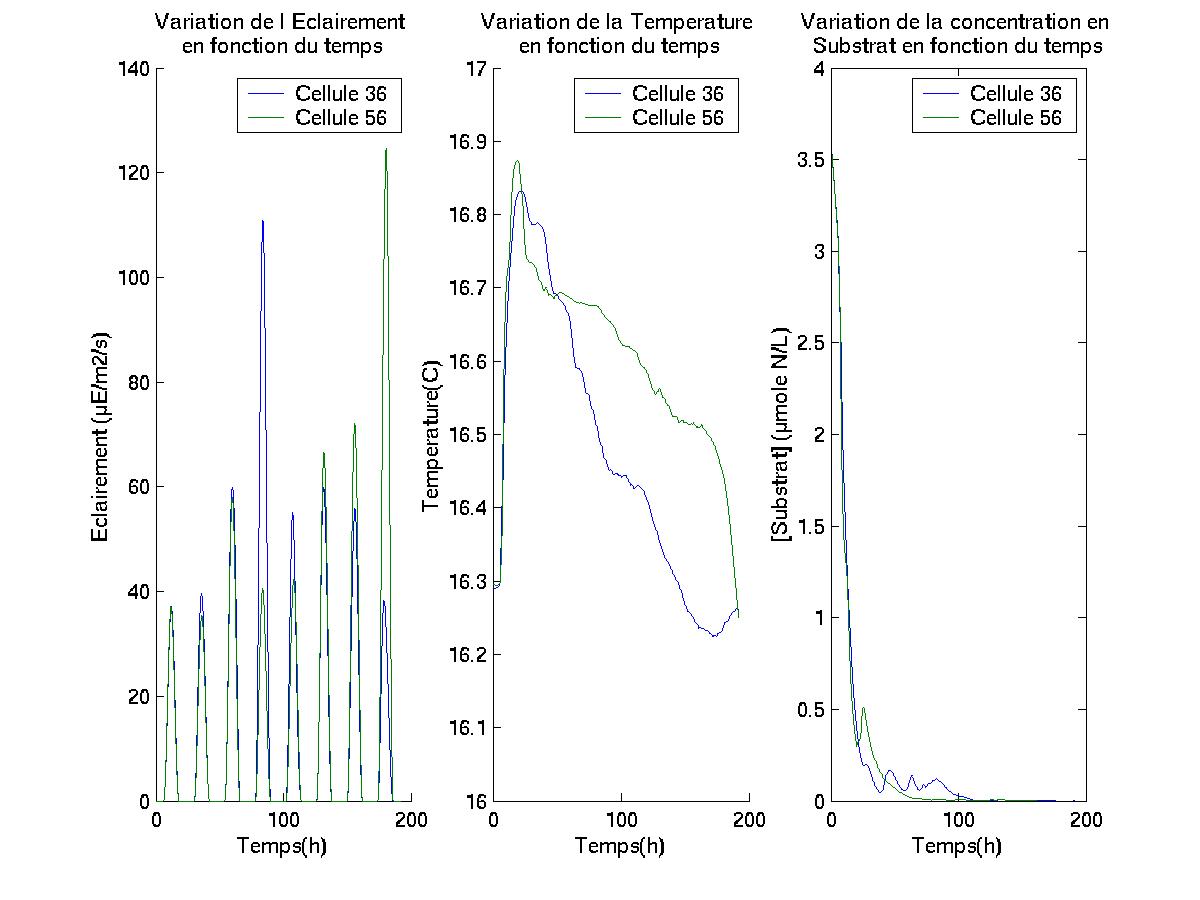
Il apparaît que les courbes caractérisant les facteurs physico-chimiques rencontrés par le parangon de la classe A et par le parangon de la classe 1 sont particulièrement proches, voire analogues sur les plans quantitatifs et qualitatifs. Au premier abord, les conditions d’éclairement peuvent sembler différer; en fait, elles sont similaires puisque les cellules 36 et 56 ont toutes deux été soumises à un pic d’éclairement durant la simulation, mais à des instants simplement translatés sur le plan temporel. La concentration en Substrat dans le milieu a soit évolué entre ces deux instants, mais l’importance de ce point est toute relative dans la mesure où les pics d’intensité lumineuse sont de courtes durées.
Le second graphe montre que les deux cellules ont été soumises à des températures quasi identiques: à son apogée, l’écart entre les deux courbes n’est que de l’ordre de 3 dixièmes de degrés Celsius.
Enfin, les concentrations en Substrat des eaux rencontrées par les deux cellules étaient tout à fait égales.
Par conséquent, la méthode de classification CQT a permis de constituer une classe de trajectoires caractéristique de conditions physico-chimiques que l’on pourrait assimiler à celles caractérisant une classe déterminée par la méthode CQL.
Cet état de faits signifie que la reconstitution des variations de l’éclairement, de la température, et de la concentration en Substrat, auxquelles ont été soumises les parangons des classes 1 et A, permettrait de récréer en chémostats, les caractéristiques physico-chimiques, tant sur le plan quantitatif que sur le plan qualitatif, susceptibles d’être rencontrées par 34 % de cellules de phytoplancton évoluant dans un upwelling et dont la distribution initiale au sein de celui-ci serait analogue à celle de la simulation menée.
· Le fait d’avoir détecté la quasi similitude des trajectoires (d’un point de vue physico-chimique) des parangons des classes 1 et A, m’a permis de poursuivre mon étude comparative selon une méthodologie nouvelle.
En effet, les classes A, B, C et D, de par la manière dont elles ont été déterminées, sont nécessairement " distinctes " deux a deux (c’est à dire qu’il n’est pas concevable que les trajectoires de leurs parangons respectifs soient analogues); il est donc inutile de tenter de les comparer entre elles. Cette remarque est également applicable au cas des classes 1, 2, 3, et 4.
Traduisons ces faits de la manière suivante:
 et
et 
 et
et 
NB: le terme de comparaison à inscrire entre chacune des
classes étant encore inconnu, remplaçons le par le symbole
arbitraire "?".
| A ce stade, sans hypothèse supplémentaire sur les autres classes, il me restait donc 9 comparaisons à effectuer: |  |
 |
 |
La comparaison deux à deux des trajectoires (concernant la concentration en Substrat, l’Eclairement, et la Température) des parangons de chacune des classes explicitées ci-dessus (graphes fournis en Annexes 9 à 15), n’a révélé aucune analogie.
Par conséquent, il apparaît que les classes 2, 3 et 4 ont
été déterminées à partir de critères
purement quantitatifs, et que la constitution des classes B, C et D est
basée sur des critères purement qualitatifs.
Conclusion
L’analyse des données relatives aux conditions physico-chimiques rencontrées par les cellules de phytoplancton a permis de constituer huit classes de trajectoires: la détermination de quatre de ces classes était basée sur des critères qualitatifs, celle des quatre autres, sur des critères quantitatifs.
Une étude comparative entre chacune de ces classes m’a permis de remarquer que les données physico-chimiques représentatives de deux classes (l’une définie par la méthode CQT et l’autre par la méthode CQL) étaient particulièrement proches, voire identiques.
Les suivis Lagrangiens des cellules de phytoplancton peuvent par conséquent être regroupés en sept classes de trajectoires:
V.B/ Limites des méthodes mises en œuvre et des résultats obtenus
· La première limite réside dans le fait que le modèle BioLov2 n’a pas fait l’objet d’une validation expérimentale; ainsi j’ai déterminé certaines constantes de ce modèle en m’appuyant sur la valeur de celles du modèle BioLov1, pour lequel la température reste constante. Le calcul mathématique mériterait d’être conforté par des observations expérimentales. Notons cependant que la validation expérimentale des modèles biologiques n’est pas une étape systématique de leur élaboration; les chémostats utilisés au LOV constituent en fait un outil susceptible de fournir un argument de validation décisif.
· La seconde limite est liée à la définition des caractéristiques physico-chimiques du cadre de simulation.
Les profils initiaux (au temps t = 0) de la température et des variables biologiques du modèle BioLov2 (N, L, C, S) sont représentatifs de ceux que l’on peut mesurer au sein d’un upwelling, puisque les valeurs que j’ai implémentées proviennent de relevés effectués lors de campagnes en mer. Pour cette raison, les cellules de phytoplancton ont fait l’objet d’un suivi Lagrangien à compter du temps t = 0. Cependant, il pourrait s’avérer intéressant, et utile, d’effectuer le suivi Lagrangien sur une même durée (192 heures) mais à partir d’un temps t où la thermocline et la chimiocline auront été modifiées par les caractéristiques hydrodynamiques propres à l’upwelling simulé par le modèle SYMPHONIE. La représentation Eulérienne de la température au temps t = 84 heures de la figure IV.11, nous a en effet montré les modifications majeures, induites par les forçages propres à l’upwelling de ce modèle, que peut notamment subir le profil de la température.
Une classification, portant sur les suivis Lagrangiens des cellules
menés à partir d’un temps t pour lequel les conditions physico-chimiques
du milieu auraient atteint un régime moins instable, pourrait donner
une importance moindre au positionnement initial des cellules de phytoplancton.
La classification des trajectoires par familles proposée en IV est
en effet fortement liée aux positions initiales des cellules de
phytoplancton (cela est visible au numéro porté par les cellules
regroupées dans une même classe, le numéro affecté
aux cellules étant lui même représentatif de la positon
initiale de la cellule: voir la distribution initiale de l’ensemble des
cellules suivies, fournie en Annexe 6).
· Le renouvellement des nutriments dans le milieu de simulation est un point pouvant lui aussi prêter à discussion. Dans l’étude que j’ai menée, une concentration initiale en Substrat était attribuée à différentes " couches " de la colonne d’eau. Ce Substrat était ensuite consommé par le phytoplancton et déplacé en raison des phénomènes d’advection et de diffusion. Aucun apport de nutriments n’avait lieu au cours de la simulation; en ce sens, le cadre de simulation était fermé, ce qui constitue une différence notable avec les océans, qui sont des écosystèmes ouverts.
· Enfin, il me parait fondamental
de mentionner que les classifications proposées s’appuient sur deux
seules natures de critères. Les types de critères utilisés
pour constituer les familles de trajectoires ne peuvent aucunement prétendre
constituer une liste exhaustive des critères adéquats de
classification. Par ailleurs, nous ne saurions définir le critère
de classification qui soit le plus approprié pour déterminer
des classes caractérisées par les conditions physico-chimiques
ayant les influences les moins similaires sur l’activité biologique
du phytoplancton.
V.C/ Perspectives pour la poursuite du projet
Le couplage du modèle hydrodynamique SYMPHONIE au modèle biologique BioLov2 m’a permis de proposer une première classification des trajectoires de cellules de phytoplancton évoluant au sein d’un upwelling. Les méthodes de classification sont cependant perfectibles. Notamment, une réflexion pourrait être engagée pour déterminer la méthode la plus adéquate pour effectuer une classification basée sur la valeur de la courbure des trajectoires simulées (en terme de concentration en Substrat, d’Eclairement et de Température).
L’étude que j’ai menée avait pour cadre de simulation un upwelling " académique ". Ainsi, la bathymétrie du domaine notamment, ne peut être considérée comme très représentative de celle des fonds marins dans lesquels les upwellings prennent naissance. Un cadre de simulation plus réaliste pourrait être désormais défini pour prétendre reconstituer avec davantage de précisions le milieu dans lesquels les cellules de phytoplancton évoluent dans les océans. Par ailleurs, les upwellings ne sont qu’un type de phénomène hydrodynamique côtier. Il serait nécessaire, à l’avenir, de coupler un modèle biologique à un modèle hydrodynamique capable de reconstituer les caractéristiques hydrodynamiques de l’ensemble des phénomènes prenant naissance, d’une part, à proximité des côtes (zones où la densité de phytoplancton est la plus notable), mais également en mer hauturière. En effet, chacun de ces phénomènes influence la répartition des nutriments dans la colonne d’eau, ainsi que le profil de la température; le taux de Carbone fixé lors de la production primaire diffère par conséquent selon les caractéristiques hydrodynamiques du milieu considéré. Il faudra par conséquent, à l’avenir, reconstituer en chémostats, les conditions physico-chimiques susceptibles d’être rencontrées par des cellules de phytoplancton évoluant au sein de l’ensemble des phénomènes hydrodynamiques prenant naissance dans les océans. L’étude que j’ai menée pourrait donc être réitérée autant de fois qu’il existe de caractéristiques hydrodynamiques " types " dans les océans.
Par ailleurs, le modèle biologique BioLov2 est un modèle de croissance algale paramétrisé pour une seule espèce de phytoplancton (Rhodomonas salina). L’écosystème océanique est remarquable sur le plan de sa biodiversité...Le modèle BioLov2 pourrait, à l’avenir, faire l’objet d’une paramétrisation pour plusieurs espèces de phytoplancton. Les travaux que j’ai menés (couplage, mise en œuvre de la simulation et classification) seraient alors réitérés et comparés aux résultats qui ont été présentés ici, en vue de tester la sensibilité de la classification au modèle biologique utilisé.
Sur le long terme, le projet SEMPO s’inscrit dans une perspective beaucoup
plus vaste, située au centre de l’une des préoccupations
environnementales actuelles majeures: l’étude de ce qui est communément
nommé " l’effet de serre ". En effet, le dioxyde de Carbone constitue
le principal gaz à effet de serre produit par l’activité
humaine. L’estimation de la quantité de Carbone absorbée
par le phytoplancton, à l’échelle océanique, lors
de la photosynthèse, sera l’une des données qui permettra
d’estimer la vitesse d’élévation du taux de Carbone dans
l’atmosphère terrestre. La connaissance de cette donnée permettrait
alors de mesurer l’importance des modifications climatiques qui pourraient
se produire à l’échelle planétaire, ainsi que la rapidité
à laquelle de tels changements seraient susceptibles de survenir.
Conclusion
Le développement, puis l’utilisation du modèle hydrodynamique SYMPHONIE couplé au modèle de croissance algale BioLov2 m’a permis de simuler les trajectoires, sur une durée de 192 heures, de 100 cellules de phytoplancton réparties dans un milieu reconstituant les caractéristiques d’un upwelling sur les plans hydrodynamique et biogéochimique. Le cheminement des cellules au sein de l’upwelling fut caractérisé par l’évolution de trois variables physico-chimiques auxquelles les cellules avaient été soumises: la concentration en Substrat, l’Eclairement, et la Température. J’ai alors effectué une classification par familles des trajectoires. Pour cela, j’ai mis en œuvre deux méthodes: l’une permettant de regrouper les cellules au sein d’une même classe au regard des similitudes d’ordre qualitatif de l’évolution des variables physico-chimiques caractérisant leurs trajectoires (méthode CQL), et l’autre réunissant les cellules lorsque l’évolution de ces mêmes variables présentait des similitudes d’ordre quantitatif (méthode CQT). Chacune de ces deux méthodes m’a permis de déterminer quatre classes de trajectoires. L’étude comparative des conditions physico-chimiques rencontrées par le parangon de chacune de ces classes m’a permis de confondre deux classes, obtenues pour l’une par la méthode CQL, et pour l’autre par la méthode CQT. Au total, sept classes de trajectoires ont donc été finalement isolées. J’ai ainsi déterminé les évolutions temporelles de la concentration en Substrat, de l’Eclairement, et de la Température, caractérisant chacune de ces familles. La reproduction, en chémostats, de l’évolution de ces variables permettra de reconstituer, in vitro, les caractéristiques physico-chimiques du milieu marin susceptible d’être rencontré par des cellules de phytoplancton évoluant au sein d’un upwelling.
L’étude que j’ai menée a donc permis de fournir une première série de données intéressant la poursuite du projet SEMPO. Cependant, les méthodes et moyens mis en œuvre pour obtenir ces résultats demeurent perfectibles. Notamment, les thermoclines et chimioclines initiales caractérisant le milieu de simulation étaient représentatives de celles observables dans des cas d’upwellings réels, car définies sur la base de relevés provenant de mesures effectuées lors de campagnes en mer; pour cette raison, les suivis Lagrangiens des cellules ont été menés à partir d’un temps t = 0, pour lequel le profil de la température et les distributions verticales des variables biologiques prises en compte par le modèle BioLov n’avaient pas encore été soumis aux forçages hydrodynamiques propres à ceux de l’upwelling simulé par le modèle SYMPHONIE. Des représentations Eulériennes de la température et des variables biologiques sus- citées ont démontré qu’une phase transitoire avait lieu, durant laquelle les profils de ces paramètres physico-chimiques étaient particulièrement modifiés par l’hydrodynamisme du modèle SYMPHONIE, et précédant l’instauration d’un régime moins instable. Par conséquent, à l’avenir, il pourrait être judicieux d’effectuer les suivis Lagrangiens des cellules de phytoplancton à compter d’un temps t où le régime transitoire a pris fin. D’autre part, une paramétrisation du modèle biologique avec plusieurs espèces de phytoplancton (et non une seule, tel qu’il est actuellement le cas) serait un premier pas vers la prise en considération de la considérable biodiversité de l’écosystème océanique. Par ailleurs, le milieu de simulation n’est soumis à aucun apport extérieur de nutriments, ce qui lui confère, de ce point de vue, les caractéristiques d’un système fermé, et constitue par là même une différence notable avec les océans, qui sont des écosystèmes ouverts. Enfin, les " types " de critères utilisés pour constituer les familles de trajectoires ne peuvent aucunement prétendre constituer une liste exhaustive des critères adéquats de classification, et il apparaît fort ambitieux de tenter de trouver le critère de classification qui soit le plus approprié pour déterminer des classes caractérisées par les conditions physico-chimiques ayant les influences les moins similaires sur l’activité biologique du phytoplancton. Cependant, les études expérimentales qui seront menées en chémostats permettront d’observer le degré de similitude entre les réponses du phytoplancton aux conditions physico-chimiques imposées, caractéristiques de chacune des classes établies, et de tester ainsi la pertinence de la classification proposée.
A l’avenir, la poursuite du projet SEMPO devra passer par la définition
de cadres de simulations plus réalistes, reconstituant les caractéristiques
hydrodynamiques et biogéochimiques de l’ensemble des phénomènes
prenant naissance, d’une part, à proximité des côtes,
mais également en mer hauturière. En effet, chacun de ces
phénomènes influence la répartition des nutriments
dans la colonne d’eau, ainsi que le profil de la température; le
taux de Carbone fixé lors de la production primaire diffère
par conséquent selon les caractéristiques hydrodynamiques
du milieu considéré. La mise en œuvre de telles recherches
autorisera alors d’entrevoir l’une des finalités du projet SEMPO,
à savoir l’affinement de l’estimation des flux de Carbone à
l’interface océan-atmosphère. De telles perspectives placent
ainsi ce projet au cœur de l’une des préoccupations environnementales
actuelles majeures: l’étude de l’effet de serre, et les conséquences
induites par l’accélération de ce processus sur les conditions
climatiques globales de notre planète.