Health-e-Child - IST-2004-027749 - Deliverable D.11.4

Brain Tumours

Computational Anatomy of the Brain

2. Morphometry of the Cortex Inferred from Sulcal Lines

2.1 A point-wise Line Correspondence Approach

In the context of the INRIA-associated team BrainAtlas with Paul Thompson at the Laboratory of Neuro Imaging, University of California at Los Angeles (LONI), we proposed with Pierre Fillard to infer the variability of the brain from a dataset of precisely delineated anatomical structures (sulcal lines) on the cerebral cortex. We model the first- and second-order moments of sulci by an average sulcal curve and a sparse field of covariance tensors along these curves. The covariance matrices are then extrapolated to the whole brain using a harmonic diffusion PDE on the manifold of tensor fields. As a result, we obtain a dense 3D variability map, which proves to be in accordance with previously published results on smaller samples of subjects. Statistical tests demonstrated that our model was globally able to recover some missing information. Preliminary results on the correlation between local and distant displacements indicate that the displacement of the symmetric point is correlated. Other long-distance correlations also appear, but their statistical significance still needs to be established.

Figure 3. From sulcal lines in a population to the brain variability; (left) sulcal lines of eighty subjects in green with the mean sulcal lines in red; (middle) variability measured along the mean sulcal lines (covariance matrix at one sigma); (right) the colour encodes the amount of variability everywhere on the cortex after the extrapolation of the variability tensors onto the whole 3D space, going from blue for the least variable places to red for the most varying ones. Images realised by P. Fillard.

Another way to gather statistics on inter-subject brain variability is to perform multiple deformable registrations between a reference image and subject images. We recently proposed a consistent mathematical framework called Riemannian elasticity to learn the shape deformation metric from a set of registrations and to use the result as a regularisation penalisation for new non-rigid registrations [Pennec et al, 2005, Pennec, 2006]. Other methods are currently being investigated by other groups. However, due to the very high complexity of the problem, each team is targeting specific aspects with different types of anatomical features and different statistical methods. In order to compare and combine wherever possible the different analyses, we recently initiated the INRIA Cooperative Research Initiative BrainVar with several other groups in France. We plan to investigate many sources of information: cortical landmarks like sulcal ribbons and gyri, the surface of internal structures or fibre pathways mapped from Diffusion Tensor Imaging (DTI). Individually, these sources of information provide only a partial and biased view of the whole variability. Thus, we expect to observe a good agreement in some areas, and complementary measures in other areas.

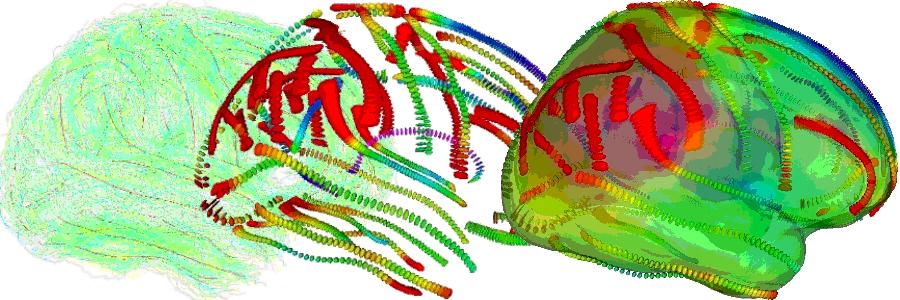
2.2 A new Correspondence-less Diffeomorphic Method

In [Durrleman et al., 2007], we apply a correspondence-less diffeomorphic method on the same dataset of sulcal lines. We kept the same set of mean lines but the model ling of both line matching and deformations is different.

Firstly, lines are modelled as currents (see [Vaillant and Glaunès, 2005] for details). The space of currents is a linear space that has many interesting mathematical properties: linear operations (addition and scaling), continuous and discrete lines are handled in the same setting with some convergence properties... . Moreover, can compute a geometric distance between two lines without any assumptions about point to point correspondences . This enables to define a 'probabilistic' line matching criterion which can be optimised to constraint the global space deformation. (see figure 4.) This framework is very general and could be used not only for lines but also for surfaces or volumes.

Figure 4. Labelled lines registration using a model based on currents. Dark blue line is transported to the green line that matches the red line. The distance between red and green lines (i.e. the precision of the matching) is computed although the sampling of each line is different, in particular no point to point correspondences are imposed.

Secondly, the large deformation framework is rooted in the paradigm of Grenander's group action approach for modelling objects [Grenander 1993, Miller et al, 2006]. The deformations are searched in a subgroup of the group of diffeomorphisms (smooth and invertible mappings). Such deformations are defined in the whole space and act on currents. In the case of curves and surfaces this action coincides with their natural geometrical transportation.

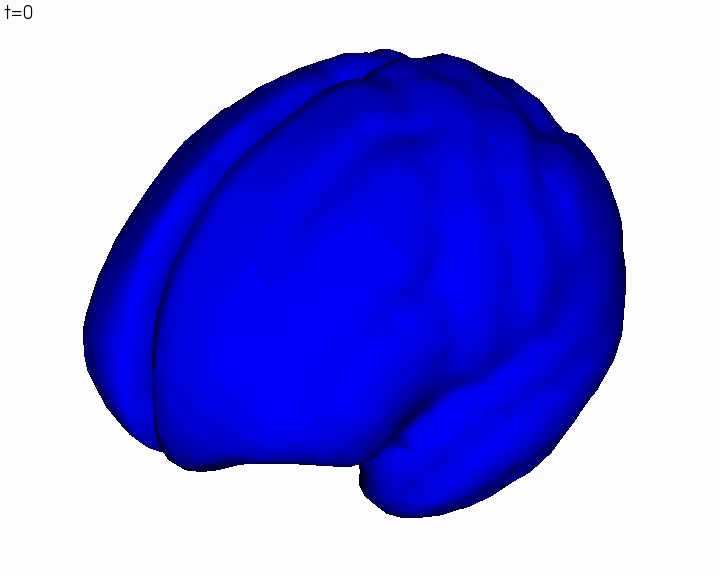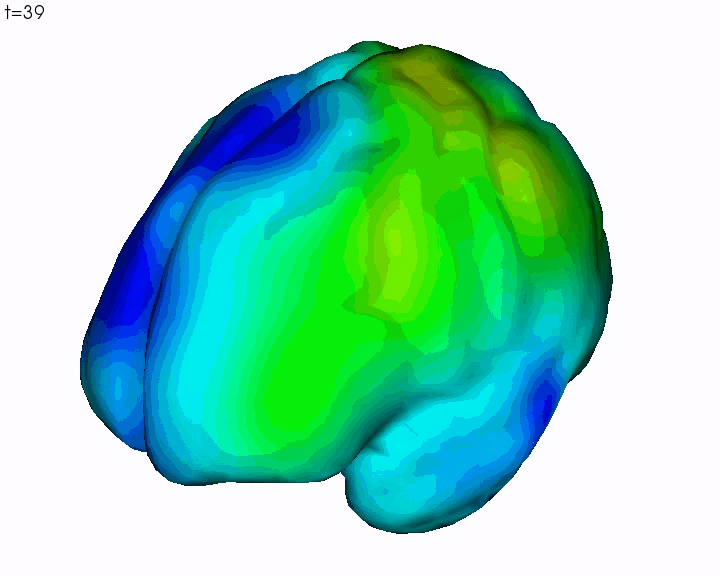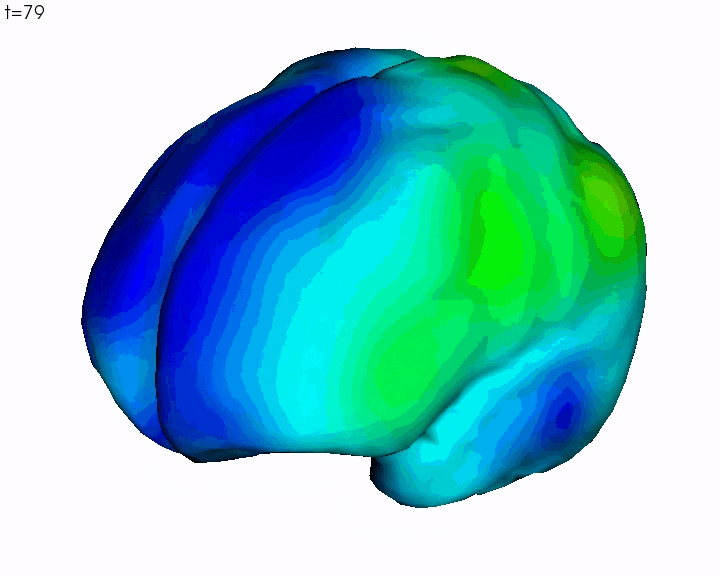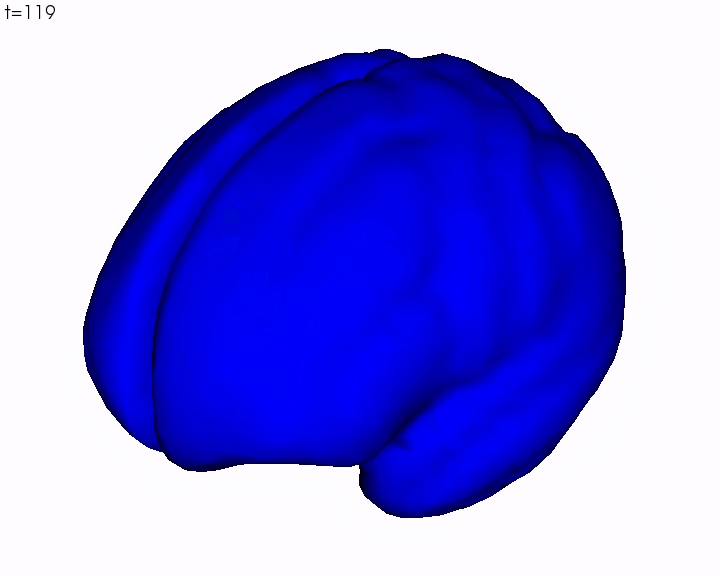
Finally, the registration is found by minimising a cost function that makes a compromise between the regularity of the diffeomorphism and the fidelity to data computed via the distance between currents. In this setting, we do not only find an optimal matching between two lines sets but also recover a global consistent deformation of the underlying biological material on which the lines are drawn. As an example the following video show the registration of a mean brain into a subject's one constrained by the sulcal lines.

This movie shows the registration of the labelled mean set of sulcal lines into one subject's labelled set. Left: dark blue lines are the mean lines; red lines are the subject's lines. The mean lines are registering into the subject's one: the transported lines are drawn in green and the trace of the diffeomorphism is drawn in light blue. Right: the deformation is not only defined on the data but also at every point of the space. For instance, the deformation constrained by the sulcal lines can be applied to the underlying brain surface. Original blue brain: a mean brain provided by P. Thompson on which the mean lines are drawn. Next frames: the deformed surface coloured according to the displacement. Copyright INRIA 2006.

This framework has the advantage of being generative. This means that we can compute samples of sulcal lines according to the Gaussian model we have learnt on the data. In particular, we can compute a tangent-PCA on the displacement field and retrieve the different modes of deformations of the database. This gives a description of the major trends of geometrical variations within the studied population. The following video shows the first deformation mode of the database: according to the Gaussian prior, this deformation is the principal trend of variations within the population.

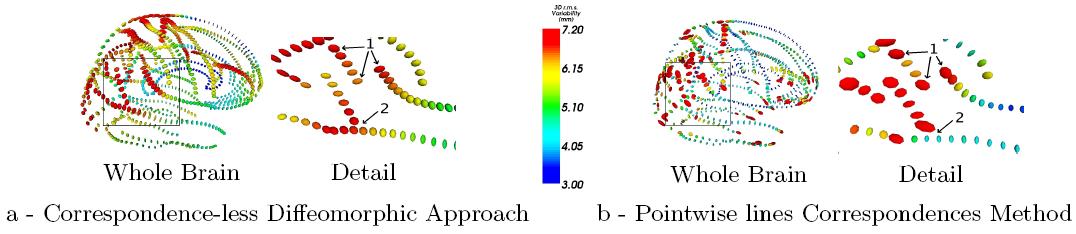
This movie shows the first mode of deformation obtained via a tangent-PCA. The original mean surface is blue and its deformation at +/- sigma is coloured according to the displacement (in mm). Copyright INRIA 2006.

2.3 Comparison of Both Methods

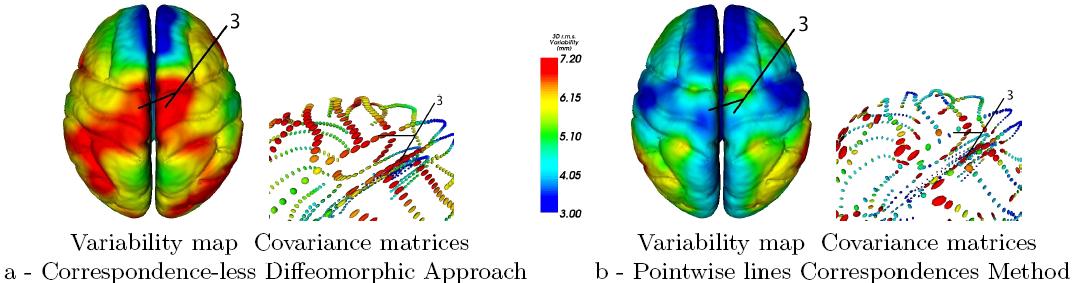
In the correspondence-less diffeomorphic approach (called here CLD) we can take advantage of the tangent space representation of the diffeomorphisms (as in [Vaillant et al, 2004]) to compute similar maps as those obtained by the previous method set up by P. Fillard and based on point-wise lines correspondences (PwLC). These maps of variability enable to emphasise the differences between both approach. These differences are explained by the hypothesis on which each method is based.

Since the CLD's approach 'integrate' the information in a spatially consistent and smooth way, the retrieved variability is naturally more regular. This is particularly visible at lines crossing or between points that belong to different lines as highlighted in figure 5. The modelling based on the currents enables also to give an alternative to the systematically under-estimated tangential variability in the PwLC's approach as explained by the figure 6. Beyond these two obvious differences, a deeper analysis can also be performed to analyse more subtle variations as presented in [Durrleman et al, 2007].

Figure 5. At every sampling points, ellipsoids represent the covariance square root of the empirical covariance matrix. In PwLC method, the extremal points are supposed to be matched leading to a high variability at lines extremities (area 1, right). This is avoided by the approach based on currents (area 1, left). In PwLC method each line is registered individually. At line crossing, the variance can vary dramatically between two close points that belong to two different lines (area 2, right). The global regularity constraint on the left hand side leads to smoother results.
Figure 6. An alternative to the aperture problem. On the variability maps, a tangential variability is measured on the top of the brain (area 3) by the CLD method while it is intentionally minimised with PwLC. On the covariance matrices of this region, we can see that the variability is mainly longitudinal. Large tensors at lines extremities with PwLC are removed before extrapolation. The remaining tensors do not capture tangential variability and lead to small variability in this area.

2.4 References