|
Presentation
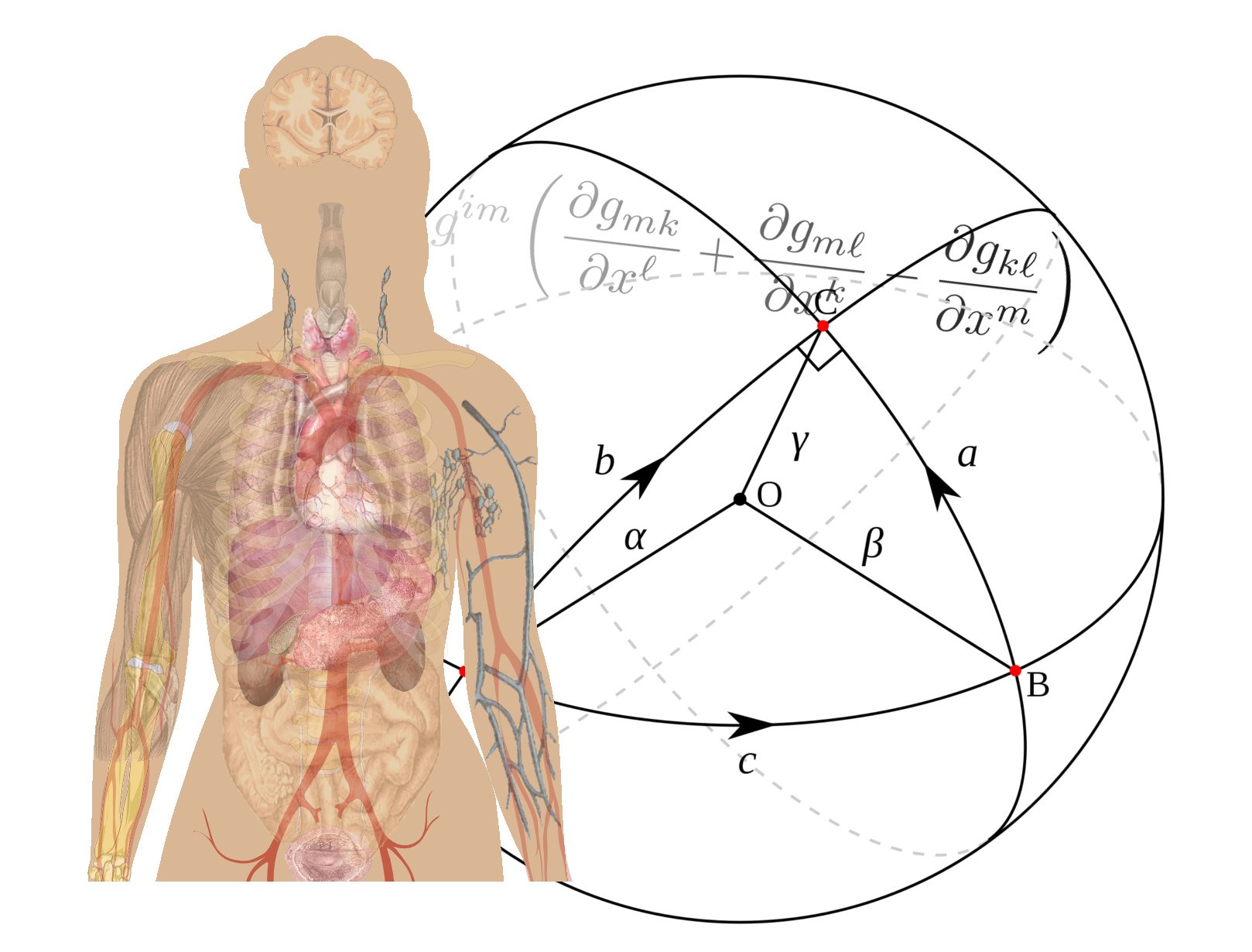
The scientific goal of the associated team is to develop the field of geometric statistics with key applications in computational anatomy.
Computational anatomy is an emerging discipline at the interface of geometry, statistics, image analysis and medicine that aims at analyzing and modeling the biological variability of the organs shapes at the population level. An important application in neuroimaging is the spatial normalization of subjects which is necessary to compare anatomies and functions through images in populations with different clinical conditions.
The research directions have been broken into three axes, the first two being methodologically driven and the last one being application driven. The first axis aims at generalizing the statistical framework from Riemannian to more general geometric structures and even non-manifold spaces (e.g. stratified spaces). The goal is to understand what is gained or lost using each geometric structure. The second axis aims at developing subspace learning methods in non-linear manifolds. This objective contrasts with most manifold learning methods which assumes that subspaces are embedded in a large enough Euclidean space. The third scientific direction is application driven with cross-sectional and longitudinal brain neuroimaging studies. The goal will be to extract reduced models of the brain anatomy that best describe and discriminate the populations under study.
Members
Principal investigators
- Xavier Pennec,
Senior Research Scientist (Directeur de recherche), Asclepios team, Inria Sophia-Antipolis, France
Xavier Pennec's research axes are about statistics on geometric data, in particular for medical image analysis, image registration and computational anatomy (statistics on normal and abnormal organs' shape across populations). This proposal is at the heart of these research axes.
- Susan Holmes,
Professor, Statistics Department, Stanford University, USA.
Pr. Holmes has been teaching at Stanford since 1998, before which she was a tenured researcher at INRA in Montpellier France, an Associate Professor in Biometry at Cornell University and a visiting Professor in Applied Mathematics at MIT. Her main focus of research is the application of nonparametric multivariate methods to biological data. She is most well known for her work on the use of topology and geometry to create a useful metric on the space of phylogenetic trees. She has also published many papers on MCMC methods and their applications in biology. Here interest in this proposal lies in the conjunction of geometry with statistics. She has more than ten collaborations with groups in the Stanford medical school and recently won an NIH Transformative Research (High Risk High Reward) award.
Other participants
- Nina Miolane, Post-doctoral fellow, Stanford, Statistics Dpt.
Nina Miolane graduated in October 2013 from the Ecole Polytechnique, Palaiseau, France, with major in Mathematics applied to Physics, and from the Master in Theoretical & Mathematical Physics (Science Quantum Fields & Fundamental Forces) at Imperial College London, UK. Her PhD at Inria Sophia Antipolis (2013-2016) was in the context of the Associated-team GeomStat under the supervision of Xavier Pennec and Susan Holmes. Nina was awarded a L'Oreal-Unesco For Women in Science National fellowship (2016) and obtained one of the Inria@SilicoValley post-doc fellowship in 2016. Due to visa issues, the starting of her Post-doc was postponed to 2017. In the meantime, to better understand the industrial needs in medical imaging, we worked as engineer in the startup Bay Labs on the subject of statistics on rigid-body poses of ultrasound probes. Staring from 2018, she holds a post-doc / lecturer position at Stanford in the Statistics department.
- Yann Thanwerdas, PhD Student, Epione team.
Yann Thanwerdas is doing his end of study internship from Ecole Central-Supelec in fall 2018 on the geometry of positive semi-definite precision matrices with applications to the statistical detection of anatomical and functional networks in brain images.
Yann will start a PhD under the supervision of Xavier pennec in January 2019 with a Cote d'Azur University excellence fellowship on statistical dimension reduction in non-Linear manifolds for
brain shape analysis, connectomics & brain-computer interfaces.
- Nicolas Guigui, PhD Student, Epione team. After a diploma from the Ecole Centrale-Supelec in 2016 and a Master in Mathematical Statistics from the University of Cambridge in 2017, Nicolas Guigui stared at PhD in Oct 2018 under the supervision of Xavier Pennec on the tatistical estimation on Riemannian and affine symmetric spaces with applications to the statistical survey of the brain anatomy.
- Marco Lorenzi, PhD, Research Scientist (Chargé de recherche), Epione team.
The research activity of Dr. Lorenzi concerns the development and study of statistical learning methods for the analysis of biomedical data, with application to the modeling of neurodegenerative disorders. His work also concerns the development of statistical tools for the analysis of data from clinical trials of disease modifying drugs. Marco will contribute to the Axis 3 of the project, based on his recent works on the meta-analysis of imaging-genetics data in distributed clinical cohorts.
Former participants
- Christof Seiler, PhD.
Dr. Seiler was a postdoctoral scholar in the department of statistics at Stanford mentored by Prof. Holmes until 2018. He obtained his joint Ph.D. degree in biomedical engineering and image processing from the University of Sophia Antipolis, France and University of Bern, Switzerland, co-advised by Dr. Pennec and Dr. Reyes (University of Bern). In 2011, he won a prestigious MICCAI young scientist award in Toronto, Canada, for his work on tree deformations for medical images. Christof Seiler left Stanford and the associated team in 2018 for an assistant professor position at the Department of Data Science and Knowledge Engineering
Maastricht University, The Netherlands.
- Loic Devillier, PhD Student, Asclepios/Epione team.
Loic Devillier started his PhD in fall 2015 under the supervision of Xavier Pennec and St걨anie Allassoniàre (CMAP, Ecole Polytechnique, Paris) on statistics on quotient spaces in the infinite dimensional setting. His expertise is on the analysis in infinite dimensions. This work is also done in collaboration with Alain Trouvé (ENS Cachan). Loic Devillier defended his PhD in December 2017. Since september 2018, he is Professor in prepartory school (PSI/PCSI) at Lycee Essouriau, France.
- Boris Gutman
Former Postdoctoral Scholar Research Associate at USC, Institute for Neuroimaging and Informatics, Los-Angeles, CA, USA.
Boris Gutman's research interest concern the brain anatomy and function, neurodegenerative disorders and their relationship with genetic factors. He is also interested in geometric methods for processing the related data (deformations for registration, Diffusion imaging with DTI or higher order models , etc.). He earned his PhD at LONI UCLA in 2013. he published more than 39 journal papers and was awarded a Michael J Fox and Alzheimer's Association fellowship for his project on Biomarkers Across Neurodegenerative Diseases, 2015-2017. Boris Gutman moved to an associate professor position of Biomedical Engineering at the Illinois Institute of Technology, Armour College of engineering.
Program and results
Computational anatomy is an emerging discipline at the interface of geometry, statistics, image analysis and medicine that aims at analyzing and modeling the biological variability of the organs shapes at the population level. The goal is to model the mean anatomy and its normal variation among a population and to discover morphological differences between normal and pathological populations. In the computational anatomy framework formalized by Grenander & Miller, the observed organ shapes are modeled as the random diffeomorphic deformation of an unknown template. Thus one need to perform statistics on infinite dimensional manifolds and Lie groups: the template can be seen as the mean shape, and the variability is encoded with the deformation variability.
An important application in neuroscience is the spatial normalization of subjects (mapping all the anatomies into a common reference system) which is used to compare anatomies and functions through images in populations and to identify the trend of one specific subject towards one of the considered populations of subjects. Statistical anatomical models are also used for the segmentation of patient images (atlas-based segmentation) thanks to the registration of generic atlases to patient specific images (personalized atlases). In this context there has been a gradual shift in the community from the use of a single atlas to the use of multiple atlases (multi-atlas segmentation methods) with important improvements of the segmentation quality. The goal of this project is to understand in which conditions the computation of the template (or more generally the mean) is well posed and to extend it to the estimation of a low-dimensional shape manifold that would mimic the multi-atlas method. From the theoretical point of view, this means quantifying the statistical efficiency (bias and variance) of the mean (however it is defined) and developing methods for subspace learning in manifolds.
The scientific goal of the associated team is to develop the field of geometric statistics with key applications in computational anatomy. The research directions have been broken into three axes, the first two being methodologically driven and the last one being application driven. The first axis aims at generalizing the statistical framework from Riemannian to more general geometric structures and even non-manifold spaces (e.g. stratified spaces). The goal is to understand what is gained or lost using each geometric structure. The second axis aims at developing subspace learning methods in non-linear manifolds. This objective contrasts with most manifold learning methods which learn (locally linear but globally non-linear) subspaces embedded in a large enough Euclidean space. The third scientific direction is application driven with cross-sectional and longitudinal brain neuroimaging studies. The goal will be to extract reduced models of the brain anatomy that best describe and discriminate the populations under study.
Statistics on manifolds beyond the Riemannian framework
In Computational Anatomy, organ shapes may be modeled as deformations of a template - i.e. as elements of a Lie group, a manifold with a group structure - or as the equivalence classes of their 3D configurations under the action of transformations - i.e. as elements of a quotient space, a manifold with a stratification. Medical images can be modeled as manifolds with a horizontal distribution. These are all manifolds with additional properties. Defining a metric or a distance to perform statistics on these manifolds might not be enough, as the metric or distance might not consistently account for the aforementioned additional structures. We develop Geometric Statistics especially beyond the now classical Riemannian and metric geometries in order to account for these additional structures. In particular, the Ph.D thesis of Nina Miolane assimilates and puts in perspective these developments.
First, organ's shapes are often modeled as deformations of a reference shape, i.e., as elements of a Lie group. To analyze the variability of the human anatomy in this framework, we need to perform statistics on Lie groups (manifolds with a consistent group structure). Statistics on Riemannian manifolds have been well studied, but to use the statistical Riemannian framework on Lie groups, one needs to define a Riemannian metric compatible with the group structure: a bi-invariant metric. However, it is known that Lie groups, which are not a direct product of compact and abelian groups, have no bi-invariant metric. In [Miolane and Pennec, Entropy 2015], we investigated if a weaker structure of bi-invariant pseudo-Riemannian metric could be sufficient for most of the groups used in Computational Anatomy. Our contribution is two-fold. First, we present an algorithm that constructs bi-invariant pseudo-metrics on a given Lie group, in the case of existence. Then, by running the algorithm on commonly-used Lie groups, we show that most of them do not admit any bi-invariant (pseudo-) metric. We thus conclude that the (pseudo-) Riemannian setting is too limited for the definition of consistent statistics on general Lie groups.
A second important generalization of the Riemannian framework that we have investigated concerns quotient spaces in which live shape data after removing the influence of some hidden transformation parameters. Statistics on shapes -and more generally on observations belonging to quotient spaces- have been studied since the 1980's. However, most theories model the variability in the shapes but do not take into account the noise on the observations themselves. In [Miolane and Pennec, GSI 2015], we show with a simple finite dimensional example that statistics on quotient spaces may be biased and even inconsistent when one takes into account the noise. This is the case for instance of one of the most used algorithms for template estimation in Computational Anatomy. Our development gives a first theoretical geometric understanding. In view of the applications, we characterize geometrically the situations when the bias can be neglected with respect to the situations when it must be corrected. The results on our toy shape spaces suggests that the main control variable is a kind of signal (seen here as the distance to the singularity) to noise ratio. In [Miolane et al, SIIMS 2016], we gave a Taylor expansion of this bias with respect to the variance of the noise on the object, for a general finite dimensional Riemannian manifold. We proposed two bootstrap procedures that quantify the bias and correct it, if needed. In [Miolane et al. 2016 ISBA], we considered the problem of learning the orbit of the template as a manifold learning problem and we showed how the Bayesian framework enables a correction in pathological cases for the Maximum Likelihood estimator.
Finally, we investigate the consequences of this statistical behavior on quotient spaces for template shape estimation in neuroimaging. The template shape estimation is interpreted as the estimation of the unique healthy brain anatomical shape of the population. But the uniqueness of a healthy brain shape may be discussed for brain shapes: for example, the distribution of the sulci on the brain surface varies significantly from one healthy subject to another. Assuming a unique anatomical brain structure may lead to a biased template. In the on-going work [Miolane et al. 2016], we present a methodology that quantifies spatially the brain template bias. This leads us to investigate the topology of the templateӳ intensity levels sets, represented by its Morse-Smale complex. We propose a topologically constrained adaptation of the template computation, that constructs a hierarchical template with bounded bias. We apply our method to the analysis of a brain template of 136 T1 weighted MR images from the Open Access Series of Imaging Studies (OASIS) database.
A third generalization of the Riemannian framework that we have investigated is sub-Riemannian geometry, where the metric is finite only in a subspace (usually non-integrable) of the tangent space. Such spaces have been used in theoretical physics as an alternative to dark matter. In computational anatomy, this would be a natural setting for modeling the as the distribution of the laminar sheets is not integrable. More generally, a sub-Riemannian structure appears in curve, surface or image interpolation and diffusion when one wants to consider first order derivatives into account. This idea has been explored in computer vision over the last years with Neuro-geometry. The aim is to model the human visual cortex and to explain human visual phenomena through modern Differential Geometry. This has resulted into new image processing algorithms for image completion, crossing-preserving smoothing, curve fitting, boundary completion, among others, where the object (curve or image intensity) is basically lifted in a larger space of position plus orientation for the processing. Generalizing these 2D algorithms to 3D medical images (and potentially higher dimensions is mathematically not straightforward. In [Miolane and Pennec, MCV 2015], we analyzed the different structures involved in 2D (Fiber bundle, group action, principal bundle) to distinguish the different notions of horizontality, verticality and geodesics used in the different papers of the field, and we show that a second level of lifting process (from oriented positions to the special Euclidean motion group) is necessary to deal with 3D curves, surfaces and images.
Geometric subspace learning
In manifold learning, one often embeds data in a large enough Hilbert space before learning a manifold structure. However, when a geometric structure is already known for the data, or when one wants to reduce the dimensionality of the data manifold in a hierarchical way, one needs to find a submanifold structure in a manifold, which is a harder problem.
One way to address this problem is to generalise Principle Component Analysis on manifolds by exploring alternatives to Principle geodesic analysis (PGA) or tangent PCA that remains well defined for other types of geometric structures (affine connection geometry, stratified spaces). In Riemannian manifolds, tangent PCA is often sufficient for analysing data which are sufficiently centred around a central value (unimodal or Gaussian-like data), but fails for multimodal or large support distributions (e.g. uniform on close compact subspaces). Instead of a covariance matrix analysis, Principal Geodesic Analysis (PGA) and Geodesic PCA (GPCA) are proposing to minimize the distance to Geodesic Subspaces (GS) which are spanned by the geodesics going through a point with tangent vector is a restricted linear sub-space of the tangent space. Other methods like Principal Nested Spheres (PNS) restrict to simpler manifolds but emphasize on the need for the nestedness of the resulting principal subspaces.
In [Pennec, GSI 2015], we propose a new and more general type of family of subspaces in manifolds that we call barycentric subspaces. They are implicitly defined as the locus of points which are weighted means of reference points. The affine span is then defined as the metric completion in the embedding manifold. As these definitions rely on points and do not on tangent vectors, they can also be extended to geodesic spaces which are not Riemannian. For instance, it naturally allows having principal subspaces that span over several strata in stratified spaces, which is not the case with PGA. We showed that affine spans locally define submanifolds which generalize geodesic subspaces. Like PGA, affine spans can naturally be nested, which allow the construction of inductive forward nested subspaces approximating data points which contains the Frechet mean. However, they also allow the construction of backward flags which may not contain the mean. In [Pennec MFCA 2015], we show that the affine span is a natural definition on the spheres that also generalises principal nested spheres. We also rephrase PCA in Euclidean spaces as an optimization on flags of linear subspaces (a hierarchies of properly embedded linear subspaces of increasing dimension). We propose for that an extension of the unexplained variance criterion that generalizes nicely to flags of affine spans in Riemannian manifolds. This results into a particularly appealing generalization of PCA on manifolds, that we call Barycentric Subspaces Analysis (BSA).
Practical implementation of geometric statistics: the geomstats library
The Python package geomstats is an open-source package for computations of Riemannian geometry in Machine Learning. The package gathers several codes from the associated team and aims at becoming the reference library to implement geometric statistics procedures, seamlessly accessible in a natural Scikit-learn machine learning environment. Nina Miolane created the library in 2018, in the framework of the Associated team GeomStats. Because it is a unique tool to promotes reproducible research in geometric statistics, we decided in 2019, to reorient all the efforts of the associated team to further push the developments and to make this library the flagship result of our collaboration. This library is also currently becoming the main development environment of the ERC G-Statistics research group. The ambition is to make “geomstats” one of the go-to packages in our field.
We organized two hackathons of one week in 2020 in January and March (gone virtual due to the lock-down) that gathered about 12 researchers from different communities coming from France, Germany, USA. This demonstrated the interest and motivation of the developers. The code is available on git-hub (https://github.com/geomstats/). It counts more than 45000 lines of code relying on three backends (numpy, pytorch and tensorflow) to authorize efficient GPU processing. It implements the atomic operations for statistical computing on more than 15 manifolds and a few generic high-level statistical learning algorithms based on these. Contributions are processed with the usual pull request of Github and continuous integration is done with the Travis tool. PEP8 / numpy standards are enforced for the code / docstrings using the flake8 tool.
The project was presented at several international conferences (GSI, Toulouse, 2019 et Scipy, Austin, 2020) and a paper in Journal of Machine Learning Research in the software section is currently in press. The library is also used as support for scientific publications in statistics and machine leraning ( B. Hou ; N. Miolane et al, MIDL 2019 ; Chevallier et Guigui, Entropy 2020 ; X. Pennec, submitted 2020).
Exchanges
- May 2020: One week visit of N. Guigui and Y. Thanwerdas (PhD, Inria) planned at Stanford for the third GeomStat Hackathon. [canceled due to Covid-19 lock-down]
- January 13-17, 2020: One week visit of N. Miolane (Post-doc Stanford) at Inria Sophia for the first GeomStat Hackathon.
- June 9-11, 2019: One week meeting of X. Pennec and N. Miolane during the Informal Workshop on New Directions in Shape Analysis (Math in the Desert, Cedar Break, Utah, USA).
- April 8-10, 2019: Y Thanwerdas visited the Statistics Department at Stanford.
- March-December 2018: 10 month stay of Nina Miolane at Stanford Statistics Department.
- May 2018: one week visit of Boris Gutman to Sophia Antipolis.
- October/November 2017: short-term visits of Nina Miolane at Stanford Statistics Department.
- July 2017: short visit of X. Pennec to Boris Gutman and Paul Thompson at LONI, USC, Los Angeles.
- December 2016: Visit of Susan Holmes at Inria for Nina Miolane's PhD Defense.
- April to June 2016: 3 month visit of Nina Miolane at Stanford Statistics Department.
- April to June and August to December 2015: 8 month stay of Nina Miolane at Stanford Statistics Department.
- April to June 2015: 3 month visit of Xavier Pennec at Stanford Statistics Department.
Events
- Dec. 4-5 2020. X. Pennec. Keynote talk on “Geometric statistics for computational anatomy” at Recent Advances in Statistical Analysis of Imaging Data W. (American Statistical Association and FSU), USA.
- Nov. 16th, 2020. Nina Miolane presented "Geomstats: a Python package for Geometry in Machine Learning" at the Oberwolfach mini workshop "Computational Optimization on Manifolds".
- July 29th, 2020. Nicolas Guigui presented the poster "Geomstats, a Python package for Geometric Learning and Information Geometry” at the workshop SPIGL'20 at École de Physique des Houches, France.
- July 8 2020. Nina Miolane presented the paper “Geomstats: A Python Package for Riemannian Geometry in Machine Learning” at the SciPy 2020 Conference.
- June 22-26, 2020. X. Pennec was keynote speaker at the Computational Geometry Week (CG Week), Zürich, CH.
- Feb. 23-27, 2020. N. Guigui, X. Pennec and Y. Thanwerdas invited speakers at the workshop Manifold and Shape Stochastics, Sandbjerg Estate, DK.
- Sept 20, 2019: Publication of the book Riemannian Geometric Statistics in Medical Image Analysis edited by Xavier Pennec, Stefan Sommer and Tom Fletcher, 3rd volume of "The Elsevier and MICCAI Society book series". The book contains 5 introductory chapters on the methodological foundations by Xavier Pennec, Tom Fletcher, Stefan Sommer, Stephen Marsland and Marco Lorenzi, and 11 contributed chapiters on applications, including a chapter by Nina Miolane, Loic Devillier et Xavier Pennec.
- Aug-30 to Sept. 5, 2019: X. Pennec organized with the help of Alice Lebriguand the Geometric Statistics workshop in Toulouse in the framwork of the Associated team GeomStats with Stanford, the ERC G-Statistics and the thematic semester "Statistics with Geometry and Topology" of the CIMI Labex of Toulouse. The workshop featured 6 hours courses by Susan Holmes and Xavier Pennec and talks by Nina Miolane and Yann Thanwerdas. The workshop was a success with about 50 participants during a week, inlcuding of course all the active participants of the associated team GeomStats.
- Aug. 27-29, 2019: X. Pennec and N. Miolane program committee members and session chairs of the Geometric Sciences of Information conference GSI' 2019 at ENAC in Toulouse. Nicolas Guigui, Yann Thanwerdas and Nina Miolane had oral presentations. Yann Thanwerdas was nominated among the 5 running papers for the best paper award for his paper < a href="https://hal.archives-ouvertes.fr/hal-02158525">Exploration of Balanced Metrics on Symmetric Positive Definite Matrices.
- June 30-July 5, 2019: X. Pennec gave a 5h course at the 14th Peyresq summer school on signal and image processing. Y. Thanwerdas and N. Guigui participated and gave a presentation on their work.
- June 21, 2019: X. Pennec presented an introduction to Geoemtric Statistics and their application to Computational Anatomy at the Academie des Sciences in Nice and Sophia Antipolis.
- June 19, 2019: X. Pennec gave an invited présentation on Geometric Statistics at the CARS 2019 conference in Rennes.
- Mai 27, 2019: X. Pennec gave a presentation on barycentric subspaces in manifolds at the Mathematics of learning seminar of the Institut Mathematique de Toulouse.
- April 1-20, 2019: X. Pennec, Y. Thanwerdas and N. Guigui participated to the IPAM program on Geometry and Learning from Data in 3D and Beyond. X. Pennec gave a 1h presentation at the Workshop I: Geometric Processing and visited Paul Thompson at USC.
- March 18, 2019: seminar of X. Pennec a DIKU (Copenhague, DK) on "Geometric Statistics beyond the Riemannian structure and beyond the mean".
- Dec. 10, 2018: X. Pennec and N. Miolane invited speakers at the Banff International Research Station, Canada. Workshop on Shape Analysis, Stochastic Geometric Mechanics and Applied Optimal Transport.
- July 16-22, 1018: X. Pennec invited speaker at the Workshop on New Directions in Shape Analysis (Math in the Black Forest).
- July 15, 2018: N. Miolane invited speaker at the International Conference of Machine Learning (ICML), Workshop Geometry in Machine Learning (GiMLi), Stockholm, Sweden.
- June 2018: GeomStat meeting in Paris (S. Holmes and X. Pennec) on the occasion of the invited talk of Susan Holmes at the Starting Conference of the Laboratoire de Probabilités, Statistique et Modélisation (LPSM) in Paris.
- May 2018: X. Pennec was awarded an ERC Advanced Grant (PE1) G-statistics #786854 on the Foundations of Geometric Statistics and Their Application in the Life Sciences. Read the Inria@SiliconValley interview.
- May 19, 2018: N. Miolane invited speaker at Baltimore, USA. Seminar of John Hopkins University, Center of Imaging Science.
- May 3, 2018: Nina Miolane received the second prize (special mention) for the AFRIF (french association for shape interpretation and recognition) PhD prize.
- April 22-18, 2018 : X. Pennec first invited speaker of the Nonlinear Data: Theory and Algorithms meeting of the Mathematisches Forschungsinstitut Oberwolfach, DE.
- Jan. 28, 2018: X. Pennec and N. Miolane invited speakers at the Statistics for Data with Geometric Structure Meeting of the Mathematisches Forschungsinstitut Oberwolfach, DE.
- January 15-17, 2018 : X. Pennec invited speaker at Mathematics and Image Analysis (MIA 2018), Berlin, DE.
- Dec. 20, 2017: N. Miolane speaker at Goettingen Statistics Seminar. Goettingen, DE.
- Dec. 16, 2017: N. Miolane speaker at the 10th International Conference on Computational and Methodological Statistics (CMStatistics 2017).
- Nov. 16, 2017: N. Miolane invited speaker at Cambridge, UK. Shape analysis and computational anatomy workshop.
- Dec. 13, 2017: N. Miolane speaker at BioMedIA Seminar, Dpt of Computing, Imperial College London, UK
- Nov. 20-24 2017: X. Pennec invited speaker at Computational Brain Connectivity Mapping Winter School Workshop (CoBCoM 2017) Juan-les-Pins, France.
- Nov. 20, 2017: PhD defense of L. Devillier at Inria Sophia-Antipolis.
- Oct. 23, 2017: L. Devillier seminar at the Probability and Statistics seminar of the Alexander Grothendieck Mathematical Institute in Montpellier, FR.
- Sep. 23, 2017: N. Miolane speaker at the American Math. Soc. (AMS) Sectional Meeting, Orlando, USA.
- July 21, 2017: X. Pennec keynote spekaer at the 3rd Int. W on Differential geometry in Comp. Vis. and Machine Learning (DIFF-CVML), Hawaii, USA.
- Jun 2017 : L. Devillier speaker at Inf. processing in Medical Imaging (IPMI 2017), Boon, NC.
- December 16, 2016: PhD defense of Nina Miolane, Inira Sophia-Antipolis.
- October 27, 2016: X. Pennec keynote speaker at the VIth Int. RFMI Workshop (RFMI 2016), Sidi Bou Said village. Tunisia.
- October 12th, 2016: Nina Miolane received a L'Oreal-UNESCO Fellowship for Women In Science 2016.
- October 10, 2016: Xavier Pennec speaker of the Colloquium of the Dieudonné (LJAD) Lab, Nice University.
- August 24, 2016: X. Pennec invited speaker at Int. W. on Geometry, PDE's and Lie Groups in Image Analysis, Eindhoven (NL).
- August 15-19, 2016: X. Pennec invited speaker at W. on Geometry and Stochastics of Nonlinear, Functional and Graph Data, Bornholm (DK),
- July 11-12, 2016: X. Pennec invited speaker at 12th IEEE IVMSP Workshop 2016, Bordeaux (FR).
- June 10th, 2016: Xavier Pennec and Nina Miolane panelists at Int. Conf. on Digital Sciences and Technologies for health (Future en Seine Festival, Paris).
- June 7th, 2016: Nina Miolane: speaker at Statistics Department Seminar, Stanford University.
- April 4-6, 2016: Xavier Pennec invited speaker at Statistical Analysis of Manifold-Valued Data and Beyond: Nottingham workshop, Nottingham, UK.
- November 2, 2015: Nina Miolane speaker at the de Probability and Statistics Seminar of the Alexander Grothendieck Mathematical Institute in Montpellier
- June 4 2015: Seminar of X. Pennec at the Center for Health Sciences, SRI international, Menlo Park, USA, June 4 2015.
- April 21, 2015: X. Pennec speaker at the Statistics Department Seminar, Stanford University
Workshop and conferences organized
- October 19-22, 2020: Geomstats coding week in Sophia Antipolis.
- Annual mathematical workshop on the geometry of shapes 2020 (Math in the Cloud), planned at La Minière de Vallauria, Tende, 06 France, and gone virtual due to the pandemics. June 29 to July 10, 2020 (X. Pennec organizer, participation of 25 people including talks by Y. Thanwerdas, N. Miolane and N. Guigui).
- March 30-April 3, 2020: Second GeomStats Hackathon in Paris [transformed to virtual], regrouping 10 people.
- January 13-17, 2020: first GeomStats Hackathon in Sophia Antipolis, regrouping 12 people.
- Geometric Statistics workshop, Toulouse, FR, Aug-30 to Sept. 5, 2019 (X. Pennec organizer, X. Pennec, S. Holmes, N. Miolane and Y. Thanwerdas speakers, N. Guigui participant).
- Geometric Sciences of Information GSI'2019, Aug. 27-29, 2019 (X. Pennec and N. Miolane program committee members and session chairs, N. Guigui, Y. Thanwerdas and N. Miolane speakers).
- Geometric Sciences of Information GSI'2017, Paris, FR, Nov 2017. (X. Pennec, S. Holmes and N. Miolane members of the Scientific Committee, X. Pennec session chair and speaker).
- Topological and Geometric Structure of Information (TGSI 2017), Luminy, FR (X. Pennec co-organizer)
- Mathematical Foundations of Computational Anatomy MFCA 2017, Quebec, CA. (X. Pennec Chair).
- Workshop on Computational methods for the better understanding of human cognition and health at BIS'2017, UC Berkeley, California, June 2017 (N. Miolane organizer).
- Geometry of Shapes Workshop (Math in the Mine), June 26 - July 2 2016, Miniere de Vallauria, Alpes Maritimes, FR (Xavier Pennec Organizer, Nina Miolane and Loic Devillier participants).
- Geometric Sciences of Information GSI'2015 (Xavier Pennec and Susan Holmes members of the Scientific Committee, Xavier Pennec session chair, Xavier Pennec and Nina Miolane speakers).
- Mathematical Foundations of Computational Anatomy MFCA 2015 (Xavier Pennec General Chair, Susan Holmes member of PC committee).
- AMS Special Session on Differential Geometry and Statistics, 2015 Joint Mathematics Meetings (AMS/MAA), San Antonio, Texas, January 2015. Session organized by Susan Holmes with Xavier Pennec as Speaker.
Scientific mediation
- The TWIML AI Podcast (formerly This Week in Machine Learning and Artificial Intelligence): Geometric Statistics in Machine Learning w/ geomstats with Nina Miolane - TWiML Talk #196
- Essay in Blog Binaire, Le Monde. Miolane's anatomy. (2017).
- N. Miolane, Les maths de l'espace-temps qui décrivent et dépassent le cerveau. Interstices, Inria (2017).
- Ma thèse en 180 secondes. Le diagnostic, demain. N. Miolane second Prize of the regional selection 2017.
- October 14th, 2016: Nina Miolane invited for the emission La tete au carré on France Inter radio.
- Highschools: N. Miolane interventions at Lycee Mansart, Saint-Cyr, France (2017), College Balzac, Venissieux, France (2017) and others.
- General public talks: N. Miolane speaker at: Unesco France's Ceremony for 70th Anniversary (2016), Women Forum Global Meeting Keynote. (2016), L'Oreal-Unesco Prizes Ceremony (2016), the European Youth Debating Competition (2017), Inria's Ceremony for 50th Anniversary (2017).
Publications
PhD theses
- Nina Miolane. Geometric Statistics for Computational Anatomy. PhD Thesis. Defended on December 16, 2016. Jury: Ian Dryden (U. Nottingham, UK), Alain Trouvé (ENS Cachan, FR), Sarang Joshi (U. Utah, USA), Stephan Huckemann (U. Goettingen, DE), Susan Holmes (U Stanford, USA), Nicholas Ayache (Inria, FR), Xavier Pennec (Inria , FR).
- Loic Devillier. Consistency of statistics in quantient spaces of infinite dimension. Defended on November 20, 2017. Jury: Stéphanie Allassonnière (U. Paris Descartes, FR),
Marc Arnaudon (U. Bordeaux, FR), Charles Bouveyron (U. Cote d'Azur, FR), Stephan Huckemann (U. Goettingen, DE), Xavier Pennec (Inria, FR), Stefan Sommer (U. Copenhague), Alain Trouvé (ENS Cachan, FR).
- Hadj-Hamou, M. Beyond Volumetry in Longitudinal Deformation-Based Morphometry: Application to Sexual Dimorphism during Adolescence. December 14, 2016. Jury: O. Colliot (ICM, Paris), Ch. Barillot (IRISA, Rennes), J.-L. Martinot (Inserm U1000, Orsay), N. Ayache (Inria, FR), X. Pennec (Inria FR), R. Deriche (Inria, FR).
Books and Proceedings
- Xavier Pennec, Stephan Sommer, Tom Fletcher
Riemannian Geometric Statistics in Medical Image Analysis
Elsevier, 2019, DOI: 10.1016/C2017-0-01561-6
- Dajiang Zhu, Jingwen Yan, Heng Huang, Li Shen, Paul M. Thompson, Carl-Fredrik Westin, Xavier Pennec, Sarang Joshi, Mads Nielsen, Tom Fletcher, Stanley Durrleman, Stefan Sommer
Multimodal Brain Image Analysis and Mathematical Foundations of Computational Anatomy, LNCS volume 11846, Springer, 2019. DOI: 10.1007/978-3-030-33226-6
Journal papers
- Nina Miolane, Nicolas Guigui, Alice Le Brigant, Johan Mathe, Benjamin Hou, Yann Thanwerdas, Stefan Heyder, Olivier Peltre, Niklas Koep, Hadi Zaatiti, Hatem Hajri, Yann Cabanes, Thomas Gerald, Paul Chauchat, Christian Shewmake, Bernhard Kainz, Claire Donnat, Susan Holmes, Xavier Pennec. Geomstats: A Python Package for Riemannian Geometry in Machine Learning. Journal of Machine Learning Research, Microtome Publishing, December 2020.
- Nina Miolane, Susan Holmes, and Xavier Pennec. Topologically constrained template estimation via Morse-Smale complexes controls its statistical consistency. SIAM Journal on Applied Algebra and Geometry, 2(2):348-375, 2018.
- Xavier Pennec. Barycentric Subspace Analysis on Manifolds. Annals of Statistics, 46(6A):2711-2746, July 2018.
- Marc-Michel Rohé, Maxime Sermesant, and Xavier Pennec. Low-Dimensional Representation of Cardiac Motion Using Barycentric Subspaces: a New Group-Wise Paradigm for Estimation, Analysis, and Reconstruction. Medical Image Analysis, 45:1-12, April 2018
- Loic Devilliers, Stéphanie Allassonnière, Alain Trouvé, Xavier Pennec. Inconsistency of Template Estimation by Minimizing of the Variance/Pre-Variance in the Quotient Space. Entropy, MDPI, 2017, 19 (6), pp.28.
- Loic Devilliers, Stéphanie Allassonnière, Alain Trouvé, Xavier Pennec. Template estimation in computational anatomy: Fréchet means in top and quotient spaces are not consistent. SIAM Journal on Imaging Sciences, 2017, 10(3), pp. 1139-1169.
- Nina Miolane, Susan Holmes, Xavier Pennec. Template organ shape estimation in Computational Anatomy: Correcting an asymptotic bias. SIAM Journal of Imaging Sciences, 2017, 10(2), pp. 808-844. DOI : 10.1137/16M1084493 (2017).
- Mehdi Hadj-Hamou, Marco Lorenzi, Nicholas Ayache, Xavier Pennec. Longitudinal Analysis of Image Time Series with Diffeomorphic Deformations: A Computational Framework Based on Stationary Velocity Fields. Frontiers in Neuroscience, 10 (article 236), 2016
- Nina Miolane, Xavier Pennec. Computing Bi-Invariant Pseudo-Metrics on Lie Groups for Consistent Statistics. Entropy, MDPI, 2015, 17 (4), pp.1850-1881. DOI : 10.3390/e17041850
- Diaconis P., Seiler C., Holmes S. et al. Discussion of "Geodesic Monte Carlo on Embedded Manifolds". Scandinavian Journal of Statistics, Volume 41, Issue 1, March 2014, Pages 3-7.
Book chapters
- Xavier Pennec. Advances in Geometric Statistics for Manifold Dimension Reduction. In: Handbook of Variational Methods for Nonlinear Geometric Data. Springer International Publishing, Apr. 2020, pp. 339–359. DOI: 10.1007/978-3-030-31351-7_11.
- Nina Miolane, Loic Devilliers, Xavier Pennec
Bias on estimation in quotient space and correction methods Chap. 9 of
Riemannian Geometric Statistics in Medical Image Analysis, Elsevier, pp.343-376, 2019. DOI: 10.1016/B978-0-12-814725-2.00017-0
- Xavier Pennec
Manifold-valued image processing with SPD matrices Chap. 3 of
Riemannian Geometric Statistics in Medical Image Analysis, Elsevier, pp.75-134, 2019. DOI: 10.1016/B978-0-12-814725-2.00010-8.
- Xavier Pennec, Marco Lorenzi
Beyond Riemannian geometry: The affine connection setting for transformation groups Chap. 5 of
Riemannian Geometric Statistics in Medical Image Analysis, Elsevier, pp.169-229, 2019. DOI: 10.1016/B978-0-12-814725-2.00012-1
- Stefan Sommer, Tom Fletcher, Xavier Pennec
Introduction to differential and Riemannian geometry. Chap. 1 of
Riemannian Geometric Statistics in Medical Image Analysis, Elsevier, pp.3-37, 2020. DOI: 10.1016/b978-0-12-814725-2.00008-x
Conferences with proceedings
- Nina Miolane, Nicolas Guigui, Hadi Zaatiti, Christian Shewmake, Hatem Hajri, Daniel Brooks, Alice Le Brigant, Johan Mathe, Benjamin Hou, Yann Thanwerdas, Stefan Heyder, Olivier Peltre, Niklas Koep, Yann Cabanes, Thomas Gerald, Paul Chauchat, Bernhard Kainz, Claire Donnat, Susan Holmes, and Xavier Pennec. Introduction to Geometric Learning in Python with Geomstats. In: SciPy 2020 - 19th Python in Science Conference. Ed. by Meghann Agarwal, Chris Calloway, Dillon Niederhut, and David Shupe. Austin, Texas, United States, July 2020, pp. 48–57. DOI: 10.25080/Majora-342d178e-007.
- N. Guigui, Shuman Jia, Maxime Sermesant, and Xavier Pennec. Symmetric Algorithmic Components for Shape Analysis with Diffeomorphisms. In GSI 2019 - 4th conference on Geometric Science of Information, Toulouse, France, August 2019
- Yann Thanwerdas and Xavier Pennec. Is affine invariance well defined on SPD matrices? A principled continuum of metrics. In GSI 2019 - 4th conference on Geometric Science of Information, Proceedings of Geometric Science of Information, Toulouse, France, August 2019.
- Yann Thanwerdas and Xavier Pennec. Exploration of Balanced Metrics on Symmetric Positive Definite Matrices. In GSI 2019 - 4th conference on Geometric Science of Information, Proceedings of Geometric Science of Information, Toulouse, France, August 2019.
- Shuman Jia, Nicolas Duchateau, Pamela Moceri, Maxime Sermesant, and Xavier Pennec. Parallel Transport of Surface Deformations from Pole Ladder to Symmetrical Extension. In ShapeMI MICCAI 2018: Workshop on Shape in Medical Imaging, Granada, Spain, September 2018.
- Hou, B., Miolane N., Khanal B., Lee M., Alansary A., McDonagh S., Hajnal J., Rueckert D., Glocker B., Kainz B. Computing CNN Loss and Gradients for Pose Estimation with Riemannian Geometry. International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI). 2018.
- Xavier Pennec. Sample-limited Lp Barycentric Subspace Analysis on Constant Curvature Spaces. In Geometric Sciences of Information (GSI 2017), Geometric Science of Information, Paris, France, pages 20-28, November 2017. Springer LNCS.
- Loic Devilliers, Xavier Pennec, and Stéphanie Allassonnière. Inconsistency of Template Estimation with the Fréchet mean in Quotient Space. In Information Processing in Medical Imaging 2017, Information Processing in Medical Imaging: 25th International Conference, IPMI 2017, Boone, NC, USA, June 25-30, 2017, Proceedings, Boone, United States, pages 12, June 2017.
- Miolane, N., Pennec, X., Holmes, S. Toward a unified geometric Bayesian framework for template estimation in Computational Anatomy. World Meeting of the International Society for Bayesian Analysis (ISBA). 2016. (Young Researcher Travel Award).
- Marc-Michel Rohé, Maxime Sermesant, Xavier Pennec. Barycentric Subspace Analysis: a new Symmetric Group-wise Paradigm for Cardiac Motion Tracking. Proc of MICCAI 2016, Oct 2016, Athens, Greece. LNCS 9902 (448-456), pp.300-307.
- Stéphanie Allassonnière, Loic Devilliers, and Xavier Pennec. Estimating the Template in the Total Space with the Fréchet Mean on Quotient Spaces may have a Bias: a Case Study on Vector Spaces Quotiented by the Group of Translations. In Mathematical Foundations of Computational Anatomy (MFCA'15), Proceedings of the fifth international workshop on Mathematical Foundation sof Computational Anatomy (MFCA'15), Munich, Germany, pages 131-142, October 2015.
- Nina Miolane, Xavier Pennec. Biased estimators on Quotient spaces. Geometric Science of Information GSI 2015, Palaiseau, France, October 28-30, 2015. Springer, Lecture notes in computer science LNCS 9389.
- Nina Miolane, Xavier Pennec. A survey of mathematical structures for extending 2D neurogeometry to 3D image processing. MICCAI Workshop on Medical Computer Vision: Algorithms for Big Data (MICCAI-MCV 2015), Oct 2015, Munich, Germany.
- Xavier Pennec. Subspaces and Affine Spans in Manifolds. Geometric Science of Information. Second International Conference, GSI 2015, Palaiseau, France, October 28-30, 2015. Springer, Lecture notes in computer science LNCS 9389.
- Xavier Pennec. Barycentric Subspaces Analysis on Spheres. Mathematical Foundations of Computational Anatomy (MFCA'15), Oct 2015, Munich, Germany. pp. 71-82, 2015.
- Seiler, Rubinstein-Salzedo and Holmes, Positive Curvature and Hamiltonian Monte Carlo. Advances in Neural Information Processing Systems (NIPS), December, 2014, Montreal, Canada. ArXiv version of full paper: Curvature and Concentration of Hamiltonian Monte Carlo in High Dimensions, July 2014. (Revised in June 2015).
Software
|