Direction des Relations Internationales (DRI)

Programme INRIA "Equipes Associées"

 

BILAN TRIENNAL / THREE-YEAR REVIEW


ATTENTION : ce dossier doit obligatoirement être rédigé en anglais
Please fill in this review in ENGLISH


EQUIPE ASSOCIEE
ASSOCIATE TEAM

SHAPES

sélection / selected in year

2007

Equipe-Projet INRIA / Research team :
Ariana

Organisme étranger partenaire / Foreign Partner Institution: Florida State University

Centre de recherche INRIA / Research Center : Sophia Antipolis Mediterrannée
Thème INRIA / Scientific theme :
Perception, cognition, interaction.

Pays/Country :
USA

 

Coordinateur français/French coordinator

Coordinateur étranger/Partner coordinator

Nom, prénom /
First Name, Name

 Zerubia, Josiane

 Srivastava, Anuj

Organisme d'appartenance/ Home Institution, Department, Lab
(précisez le département et/ou le laboratoire)

 INRIA, Ariana

 Florida State University, Department of Statistics

URL

 http://www-sop.inria.fr/ariana

 http://www.stat.fsu.edu/

E-mail

 Josiane.Zerubia@sophia.inria.fr

 anuj@ani.stat.fsu.edu


La collaboration en bref / The Collaboration in brief

Titre de la thématique de collaboration / Title of the collaboration theme :

Statistical theory of configurations of shapes for analyzing aerial and satellite images

Descriptif (environ 10 lignes) / Summary (approximately 10 lines) :

The aim of this Associated Team is to combine the competences of EPI Ariana (INRIA/I3S), directed by Josiane Zerubia, in image processing, stochastic geometry, and MCMC techniques, with those of the team led by Anuj Srivastava in the Department of Statistics at Florida State University, in shape analysis and shape statistics applied to images. The synergy between the two groups via the Associated Team will allow advances in the problem of the detection of objects in high resolution satellite and aerial imagery, on the application side, as well as in the theory of shape modeling and statistics.


BILAN SYNTHETIQUE DE LA COLLABORATION / SYNTHESIS OF THE COLLABORATION

 

INRIA
Nombre/Number

Partenaire(s)/ Partner
Nombre/Number

Chercheurs seniors impliqués

Senior researchers involved

 3

 4

Post-doctorants

Post-doctoral graduates

 1

 0

Doctorants

PhD students

 2

 3

Stagiaires

Interns

 0

 1

Thèses en co-tutelle soutenues

Co-supervised defended PhD

 0

 0

Thèses en co-tutelle en cours

Current co-supervised PhD

 0

 0

Total des thèses soutenues

Global defended PhD

 1

 1

Total des thèses en cours

Global current PhD

 1

 2

Visites de l'équipe partenaire (hors colloques)

Travels to the partners (conferences not included)

 11

 9

Nombre de Publications/Number of publications

 9

 

Quels sont, selon vous, les points forts de cette collaboration et la valeur ajoutée de l'Equipe Associée ?
/ In your opinion, what are the main results and what is the added value of the Associate Team ?
(maximum 5 lignes)

The main results are: the development of the SRV representation for curves in Rn, and the associated metrics and algorithms; the combination of shape tools and differential geometry leading to successful object recognition in cluttered point clouds; the development of computationally feasible marked point processes for general object shapes. None of these results could have been achieved without the collaboration enabled by the Associated Team funding. We note that the French Space Agency CNES is interested in marked point processes for general object shapes for the analysis of satellite images.


Comment envisagez-vous l'avenir de cette collaboration ? (renouvellement de l'Equipe Associée, poursuite sur fonds propres, projet européen ou autre, arrêt de la coopération...)
/ How do you see the evolution of this cooperation (renewal of the Associate Team, european project or other-funding project, end of the cooperation...)
(maximum 5 lignes)

During the last year, the PhD work of Maria Kulikova has moved towards a fusion of the approaches to shape modeling and object extraction under investigation in Associated Team Shapes and the other Associated Team involving EPI Ariana, Odessa. When Odessa comes to an end next year, we envisage submitting a proposal for a single, new Associated Team involving all the partner teams of both Shapes and Odessa, and combining their research themes into a unified whole, stressing the commonalities and complementarities of the various approaches.

 





BILAN SCIENTIFIQUE / SCIENTIFIC REPORT

Description de l'activité scientifique de l'équipe associée et des résultats obtenus au cours des 3 dernières années : publications, communications, organisation de colloques, formation, soutenances de thèse, valorisation économique, sociale, industrielle, dépôt de brevets ... (maximum 5 pages)
Please detail the Associate Team scientific activity as well as the results obtained in the last 3 years : publications, communications, organization of conferences, training, defended PhD, valorization, patents filing. 

Scientific Results

Shape analysis of elastic curves in Euclidean spaces

This work introduces a square-root velocity (SRV) representation for analyzing shapes of curves in Euclidean spaces using an elastic metric. The SRV representation has several advantages: the well-known elastic metric simplifies to the L2 metric, the reparameterization group acts by isometries, and the space of unit length curves becomes the familiar unit sphere. The shape space of closed curves is a submanifold of the unit sphere, modulo rotation and reparameterization groups, and one finds geodesics in that space using a path-straightening approach.

The choice of a shape representation and a Riemannian metric are critically important for shape analysis and description – for improved understanding, physical interpretation, and efficient computing. This work introduces a particularly convenient representation for curves in Rn that enables a simple physical interpretation of the 'energy' of shape deformations. This representation is motivated by the well-known Fisher-Rao metric, used previously for imposing a Riemannian structure on the space of probability densities; taking the positive square-root of densities results in a simple Euclidean structure where geodesics, distances, and statistics are straightforward to compute. A similar idea was introduced by Younes [1] and later used in Younes et al. [2] for studying shapes of planar curves under an elastic metric. The representation used in our work is similar to these earlier ideas, but is sufficiently different to be applicable to curves in arbitrary Rn.

The main contributions of this research are as follows:

Publications

  1. Conference Paper: S. H. Joshi, A. Srivastava, E. Klassen and I. H. Jermyn, An Efficient Representation for Computing Geodesics Between n-Dimensional Elastic Curves, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Minneapolis, MN, June 2007.

  2. Conference Paper: A. Srivastava, I. H. Jermyn and S. Joshi. Riemannian Analysis of Probability Density Functions with Applications in Vision, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Minneapolis, MN, June 2007.

  3. Conference Paper: S.H. Joshi, A. Srivastava, E. Klassen, and I. H. Jermyn, Removing Shape-Preserving Transformations in Square-Root Elastic (SRE) Framework for Shape Analysis of Curves, Proceedings of Sixth International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition (EMMCVPR), pages 387-398, Hubei, China, August 2007.

  4. Journal Paper: A. Srivastava, E. Klassen, S. H. Joshi, and I. H. Jermyn, Shape Analysis of Elastic Curves in Euclidean Spaces, Under review at Transactions of Pattern Analysis and Machine Intelligence, revised, May 2009.

Looking for shapes hidden in two-dimensional, cluttered point clouds

We study the problem of classifying shapes in point clouds that are made of sampled contours corrupted by clutter and observation noise. Taking an analysis-by-synthesis approach, we simulate high-probability configurations of sampled contours using models learned from the training data to evaluate the given test data. To facilitate simulations, we develop statistical models for sources of (nuisance) variability: (i) shape variations within classes, (ii) variability in sampling continuous curves, (iii) pose and scale variability, (iv) observation noise, and (v) points introduced by clutter. The variability in sampling closed curves into finite points is represented by positive diffeomorphisms of a unit circle and we derive probability models on these functions using their square-root forms and the Fisher-Rao metric. Using a Monte Carlo approach, we simulate configurations using a joint prior on the shape-sample space and compare them to the data using a likelihood function. Average likelihoods of simulated configurations lead to estimates of posterior probabilities of different classes and, hence, Bayesian classification.

The process of estimating boundaries in images or videos uses low-level techniques that extract a set of primitives - points, edges, arcs, etc. - in the image plane, resulting in a cloud of primitives. Therefore, an important problem in object recognition is to (probabilistically) relate a given set of primitives to the predetermined (continuous) shape classes and to classify the shape of this set using a fully statistical framework.







(a) Data

(b) Clutter removal

(c) Ordering

(d) Classification

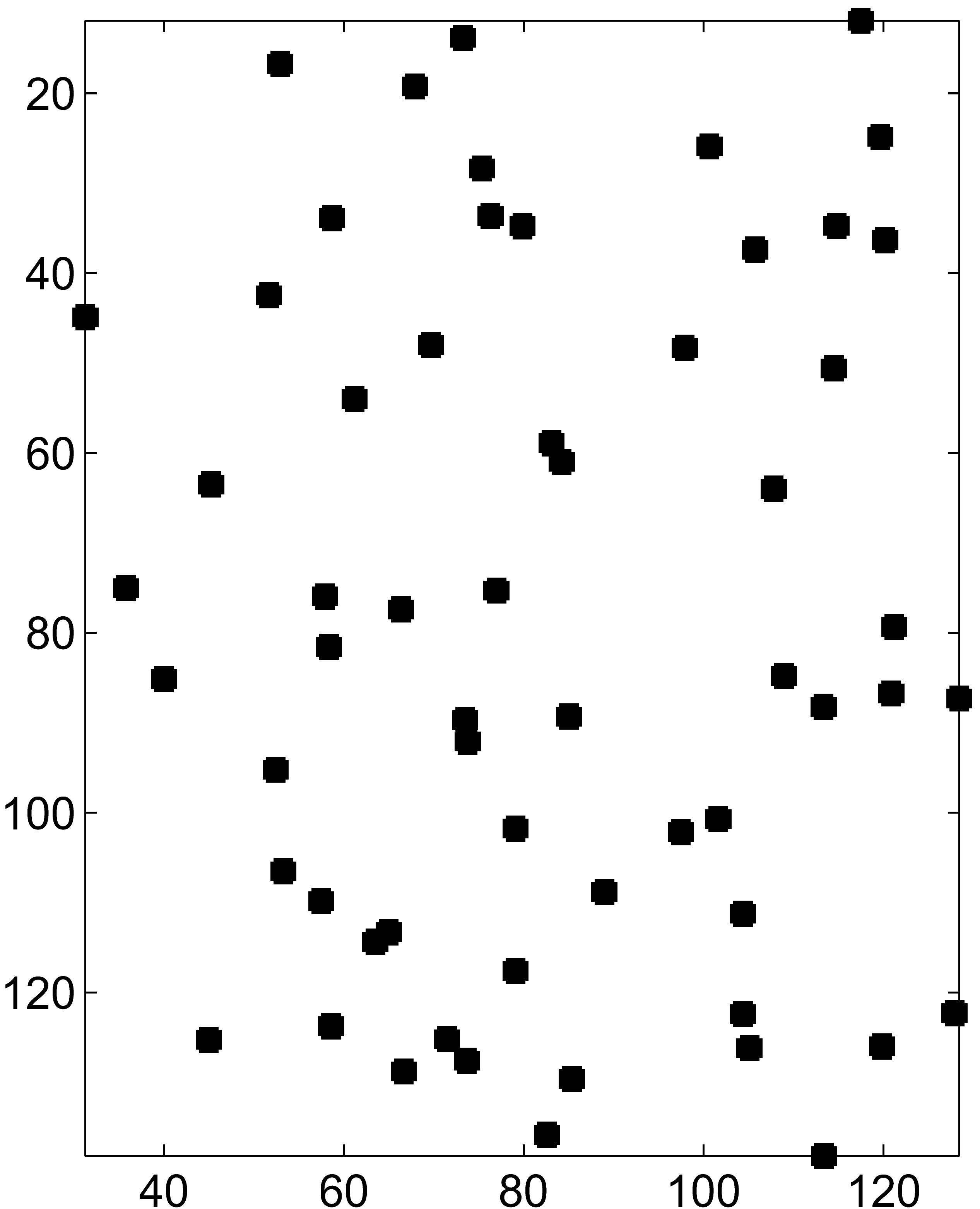
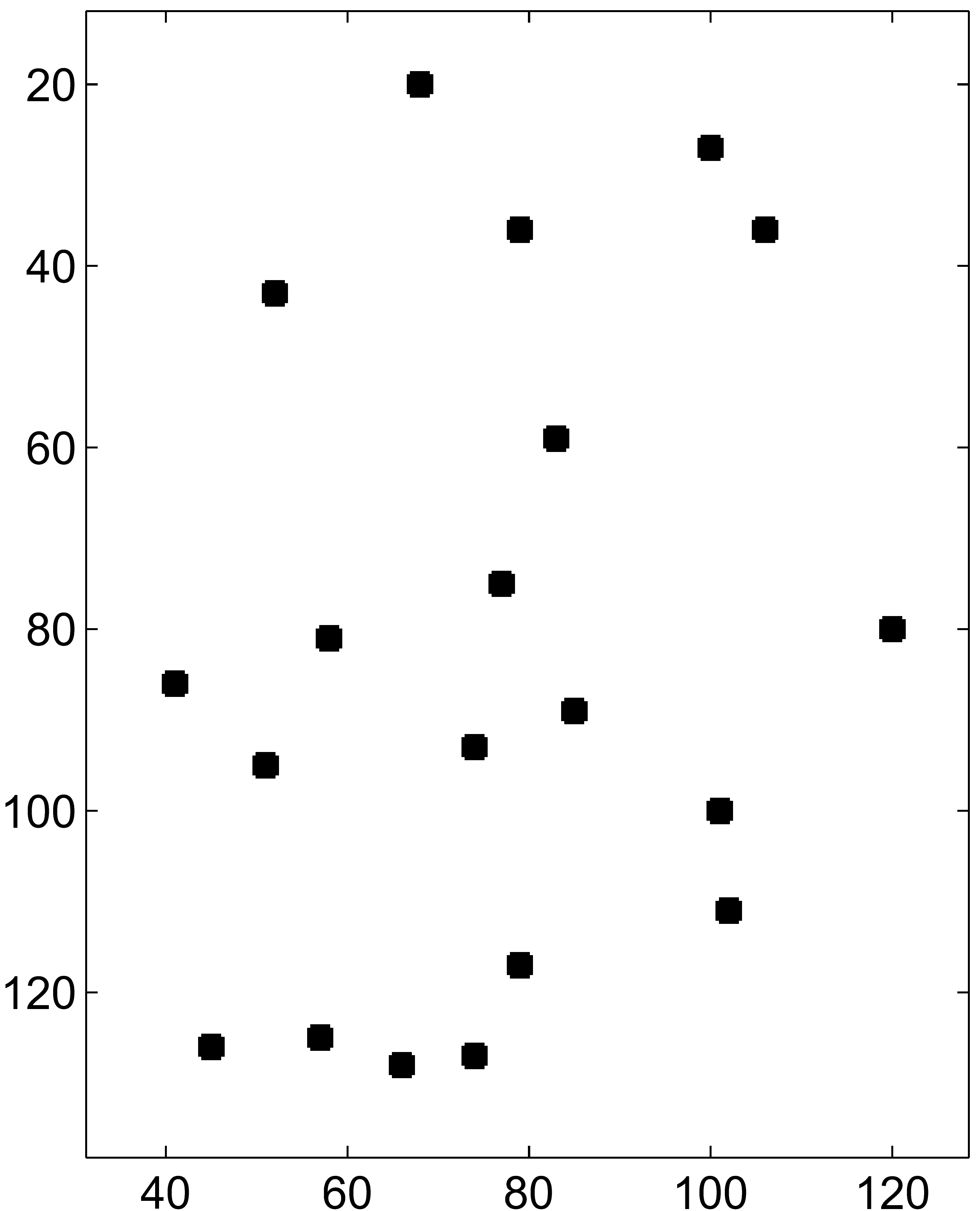
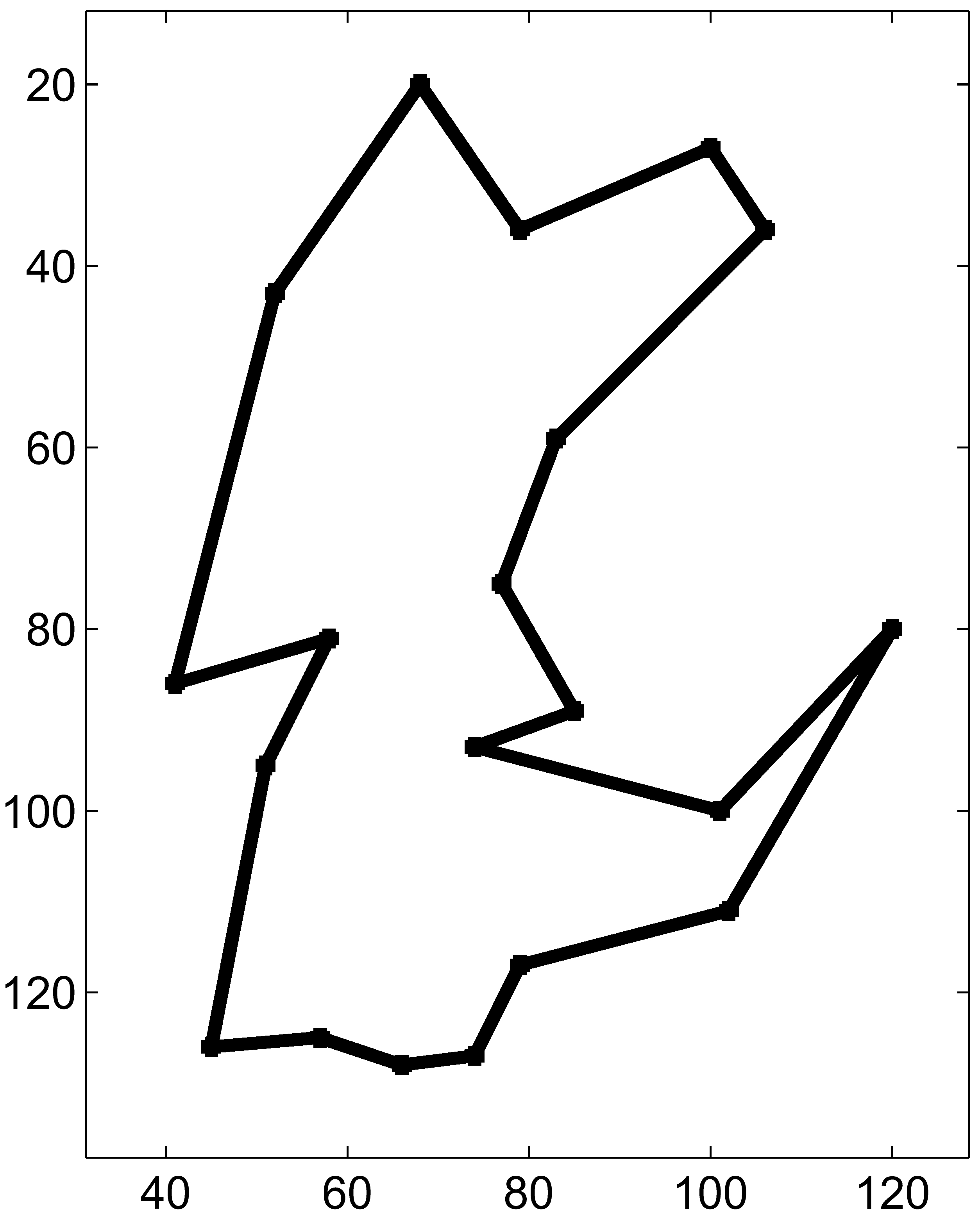
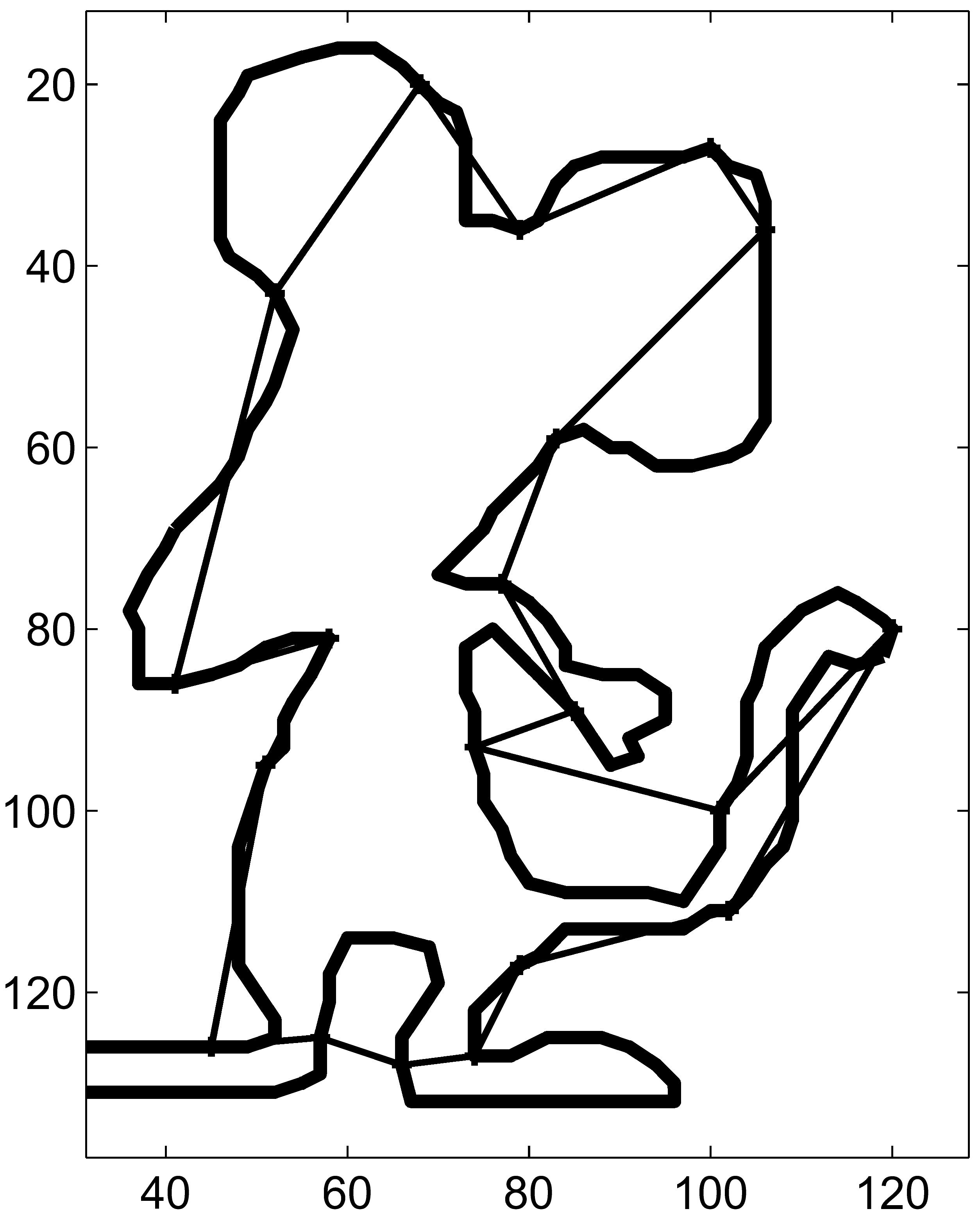
Figure 1: Problem Challenges: for the point set shown in left, the points belonging to clutter are removed. The remaining points are ordered and classified into a shape class.



Problem challenges

The biggest challenge in this problem is to select and organize a large subset of given primitives into shapes that resemble shapes of interest. The number of permutations for organizing primitives into possible shapes is huge. For example, the number of possible polygons using 40 distinct points in a plane is of the order 1047. Even if we take only 20 points, out of the given 40, to form a polygonal shape, the number of possibilities is still high ≈ 1029. To form and evaluate all shape permutations is impossible. Our solution is to analyze these configurations through synthesis, i.e. synthesize high-probability configurations from known shape classes and measure their similarities with the data. Although this approach has much less complexity compared to the bottom-up combinatoric approach, the joint variability of all the unknowns is still enormous. One has to put an additional structure into the problem by breaking down the variability into components, and probabilistically modeling the components individually. Through the examples presented in Figure 1 we will explain these components.

Bayesian Solution

We have proposed and implemented a fully Bayesian approach that follows the paradigm of analysis by synthesis. The idea is to understand a given point cloud by by synthesizing high-probability configurations of points x generated by the object from prior models on shape given class, P(q|C), and on sets of sample points on the shape given class, P(s|C). These synthesized configurations are compared with the data y using a likelihood function based on the product of a Gaussian distribution for the distances between points in x and associated points in y, and a Poisson distribution for the points in y not associated to points in x, i.e. supposed generated by the background. The likelihood is obtained by optimizing over rotations, translations, and scaling of x, and over associations between the points of x and those of y. We use the standard Euclidean registration techniques for the former and the Hungarian algorithm for the latter. We can then estimate the posterior probability for class C, P(C|y), as follows. We: (i) randomly generate a Poisson random variable n (number of sample points on the curve), (ii) generate a shape q ∼ P(q|C) from the shape model for class C, (iii) generate a sampling function (diffeomorphism of the circle creating n points on the curve starting from uniformly spaced points Un) s ∼ P(s |C), and (iv) evaluate the likelihood of the resulting point set x = q(s(Un)) by solving the association and the registration problems mentioned earlier. Averaging of the likelihood over multiple realizations of n, q and s leads to a Monte Carlo estimate of the posterior. The method works well: the posterior probabilities are typically highest for the class to which the object in the image belongs, even though the training shapes used to develop the shape models P(q|C) were distinct and sometimes quite different from the shapes present in the test images.

Publications

  1. Conference Paper: A. Srivastava and I. H. Jermyn, Bayesian Classification of Shapes Hidden in Point Clouds, Proceedings of 13th Digital Signal Processing Workshop, Marco Island, FL, January 2009.

  2. Journal Paper: A. Srivastava and I. H. Jermyn, Looking for Shapes in Two-Dimensional, Cluttered Point Cloud, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 9, pages 1616-1629, September 2009.

Tree crown classification

We have studied the improvement in object classification due to shape descriptors. The application addressed is tree species classification based on tree crown contours extracted from high resolution images. We consider a forest in Sweden where only four species occur (birch, aspen, spruce and pine). A first classification is performed using radiometric and textural features. The textural features are derived from the co-occurrence matrices. Therefore, we use first and second order statistics to describes tree crowns. We then consider the shape description proposed by Srivastava et al. [3] and the associated metric. We define some features from this shape representation by considering the geodesic distance between the considered shape and a disk. We add also some parameters characterizing the angle function of the curve describing the shape contour. We show that these shape descriptors improve tree crown classification performance.

Publications

  1. Conference paper: M. S. Kulikova, M. Mani, A. Srivastava, X. Descombes and J. Zerubia,
    Tree Species Classification Using Radiometry, Texture and Shape Based Features, Proc. European Signal Processing Conference (EUSIPCO), 2007.

Shape detection using multiple birth and death dynamics

Over the past ten years, EPI Ariana has developed a methodology based on marked point processes for the detection of a collection of objects in an image. It consist in modeling the output as a configuration of objects, each described by a small number of parameters. Numerous applications have been addressed within this framework. However, one limit of this approach lies in the simplicity of the geometric description of the objects. Disks or ellipses have been used for tree detection, rectangles for building footprint extraction or segments for road network delineation. Recently, a new optimization algorithm has been proposed that outperforms the classical RJMCMC algorithm [4]. We therefore can expect to embed more complex descriptions of objects into the marked point process. In this context, we have proposed a marked point process modeling collections of potentially arbitrary shapes. To construct the set of objects for a given image, we evolve an active contour under gradient descent starting from a disk, the radius being the mark of the point in the configuration. The energy of the active contour contains two data terms: a Gaussian term inside and outside the shape and a contrast term along the contour; and two prior terms: contour length and another based on Fourier descriptors of the shape. In this way, by varying the position and the radius of the initial circle, we generate a set of objects adapted both to the data and to the prior information contained in the energy. We then invoke the marked point process framework to address the detection of multiple objects. The associated energy includes the active contour energy and a repulsive term encouraging objects not to overlap. The final configuration is obtained by simulated annealing based on multiple birth and death dynamics. We have applied this model to tree crown extraction. In terms of object detection, the results obtained provide performance similar to marked point processes based on simple parametric objects (ellipses in this case), but with a more detailed description of individual object geometry. Therefore, simple shapes like ellipses appear to be better adapted to counting objects, whereas, for example, for classifying trees into species or to evaluate the crown size, the approach described here is more accurate.

Publications

  1. Conference paper: M. S. Kulikova, I. H. Jermyn,  X. Descombes, E. Zhizhina and J. Zerubia, Extraction of arbitrarily shaped objects using stochastic multiple birth-and-death dynamics and active contours, IS&T/SPIE Electronic Imaging, San Jose, USA, January 2010.

  2. Conference paper: M. S. Kulikova,  I. H. Jermyn,  X. Descombes,  E. Zhizhina and J. Zerubia, A marked point process model with strong prior shape information for extraction of multiple, arbitrarily-shaped objects., Proc. IEEE SITIS, Marrakesh, Morocco, December 2009.

References

[1] L. Younes, Computable elastic distance between shapes, SIAM Journal of Applied Mathematics, 58(2):565–586, 1998.

[2] L. Younes, P. W. Michor, J. Shah, D. Mumford, and R. Lincei, A metric on shape space with explicit geodesics, Matematica E Applicazioni, 19(1):25–57, 2008.

[3] A. Srivastava, S. Joshi, W. Mio and B .Liu, Statistical Shape Anlaysis: Clustering, Learning and Testing, IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(4), pages 590-602, April 2005.

[4] X. Descombes, R. Minlos and E. Zhizhina, Object Extraction Using a Stochastic Birth-and-Death Dynamics in Continuum, Journal of Mathematical Imaging and Vision, 33, pages 347-359, 2009.

Visits and Seminars

2007
2008
2009

Training

The following junior scientists visited the corresponding partner team during the lifetime of the project:

INRIA: A. El Ghoul (PhD), M. S. Kulikova (PhD), and C. Benedek (Post-doc). All of these scientists gave seminars during one or more of their visits.

FSU: S. Joshi (PhD), W. Liu (PhD), S. Kurtek (PhD), and J. Su (Master).

PhD defences

Shantanu Joshi: July, 2007. Title: Inference in Shape Spaces with Applications to Computer Vision.

Maria Kulikova: December, 2009. Title: Shape Recognition for Image Scene Analysis.



© INRIA - mise à jour le 08/07/2009