Definitions and Notations 2/3

Simulation and Optimization of marked point processes

A marked point process 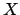$X$ is fully defined by its unnormalized density 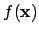$f(\mathbf{x})$ with respect to the reference measure, which is often the probability distribution of an homogeneous Poisson process. Sampling the point process is not easy, and requires using MCMC algorithm which converges to the equilibrium distribution $\mathcal{P}_{\mathit{X}}(d\mathbf{x})$ :

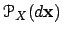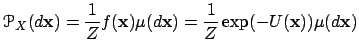$$\mathcal{P}_{\mathit{X}}(d\mathbf{x})=\frac{1}{Z}f(\mathbf{x})\mu(d\mathbf{x})=\frac{1}{Z}\exp(-U(\mathbf{x}))\mu(d\mathbf{x})$$ (4)

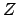where $Z$ is a normalizing constant, and 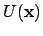$U(\mathbf{x})$ the energy of the configuration $\mathbf{x}$.

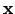In practice, our goal is to find the Maximum A Posteriori (MAP estimator) of this density, which is also the minimum of the energy. A classical Simulated Annealing scheme can be adapted to have a good estimation of this optimal configuration.