Etape 2   Mise en Correspondance de Graphes  Etape 1

Potentiels de cette première phase (modèle markovien)

L'attache aux données de ce modèle est constituée par la distance entre deux noeuds, c'est-à-dire la distance entre un pixel de l'image et un segment cartographique.

On ajoute d'un label nul $\emptyset$ à la carte pour modéliser les données cartographiques manquantes.

Ce label se trouve à une distance constante, d, de tous les noeuds .

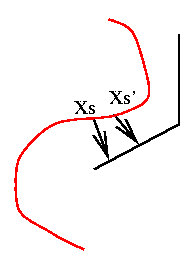
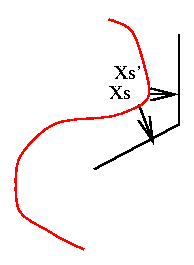
Les potentiels sur les cliques d'ordre 2  introduisent des contraintes d'homogénéïté :
 

$$V_c(x_s,x_{s'})=\left\lbrace\begin{array}{l}0 \mbox{ si......meq f(x_{s'})\\\alpha _2 \mbox{ sinon }\end{array} \right.$$  
 

	$$V_C(x_s,x_{s'})=\alpha_1$$	$$V_C(x_s,x_{s'})=\alpha_2$$

  $$0<\alpha_1<\alpha_2$$

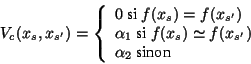
Les potentiels sur les cliques d'ordre 1 reflètent l'attache aux données :

Distance entre le pixel et le label (segment cartographique)  

L'énergie définie par la somme de tous les potentiels est minimisée par un recuit simulé avec une dynamique de Metropolis.

   
 
   
 

Octobre 1998