Next:1st
step Up:Graph
Matching Previous:Representation
of line networks
Markov Random
Fields
A family of random variables 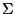 is said to be a Markov Random Field on S with respect to a neighborhood
system if and only if:
is said to be a Markov Random Field on S with respect to a neighborhood
system if and only if:
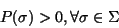
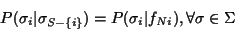
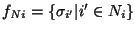 being the neighborhood system.
being the neighborhood system.
Neighborhood system for a Markov Random Field of order1
and corresponding cliques with cardinal lower or equal to 2:

Hammersley-Clifford theorem: A Markov Random Field
can be written as a Gibbs distribution,
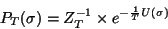
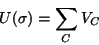
Christine Hivernat & Xavier Descombes
November 1998
![]()
![]()
![]() being the neighborhood system.
being the neighborhood system.

![]()
![]()