Previous Contents Next
Previous : Sampling the densities  Next : The MCMCML estimation algorithm 
 
The modified Geman & Yang sampler
 
We use a half-quadratic form of :
auxiliary variable b, auxiliary images Bx, By (gradients w.r.t.  x and y)

sampling triplets (X, Bx, By) in an alternated way on X and Bx, By

the pixels of Bx and By are independent
      and the law of X knowing Bx, By is Gaussian

sampling X  is made in a single pass (unlike Gibbs and Metropolis samplers),
        the processing is independent of the neighbourhood size
        which provides a fast algorithm for posterior distribution sampling.

Posterior distribution 
Posterior modified Geman & Yang algorithm
Initialization : 
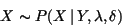
We first calculate the Fourier transform F[h4 ] and DCT[Y], and W : 
The initialization is done using the reconstructed image, obtained with the
ICM-DCT algorithm : X0 = .
Sampling Bx,By with a fixed X
The pixels b of Bx and By are independent : 
Sampling X with fixed Bx,By
The distribution of X with known B is Gaussian because 
 
$\rightarrow$ diagonalization of the covariance matrix  
          by a cosine transform  (DCT) 
          which enables to fulfill symmetric boundary conditions 
 
where R is an image whose pixels are Gaussian random variables, 
with variance 1/2.
 
Example (64x64 image) :
 
X0
 initialization 
X0 = 
XB
 
 Bx 0, By 0 
 
 
BX
 iteration 1
X1
 
XB
 
Bx 1, By 1
 
 
BX
iteration 2
X2
 
 
etc.
Ni iterations for initialization before
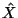reaching the equilibrum distribution
 
 

Prior distribution 

Prior modified Geman & Yang algorithm
Initialization : 
We first calculate the Fourier transform F[h4 ] and W0 : 
The initialization is done using a constant image : X0 = 0.
Sampling Bx,By with a fixed X
The pixels b of Bx and By are independent : 
Sampling X with fixed Bx, By 
The distribution of X with a known B is Gaussian because 
  
$\rightarrow$ diagonalization of the covariance matrix  
          by a cosine transform  (DCT) 
          which enables to fulfill symmetric boundary conditions
 
where R is an image whose pixels are Gaussian random variables, 
with variance 1/2.
 
 Example (64x64 sample) :
 
X0
 initialization 
X0 = 0
XB
 
 Bx 0, By 0 
 
 
BX
 iteration 1
X1
 
XB
 
Bx 1, By 1
 
 
BX
iteration 2
X2
 
 
etc.
Ni iterations for initialization before
reaching the equilibrum distribution
 
 
Previous Next
André Jalobeanu - 24 Aug 1998