R
é s u m é
 Le problème que nous abordons ici est la déconvolution
d'images satellitaires, qui sont dégradées par l'optique
et l'électronique utilisées pour leur acquisition. Les dégradations
sont connues: les images sont convoluées par un opérateur
H, et la variance du bruit N additif, blanc et gaussien,
est connue.
Le problème de déconvolution, mal posé,
doit être régularisé. Nous utilisons un modèle
de régularisation introduisant une fonction de potentiel Phi, qui
interdit l'amplification du bruit lors de la restauration tout en
préservant les discontinuités de l'image restaurée,
c'est-à-dire ses contours. Ce modèle admet deux hyperparamètres
Le problème que nous abordons ici est la déconvolution
d'images satellitaires, qui sont dégradées par l'optique
et l'électronique utilisées pour leur acquisition. Les dégradations
sont connues: les images sont convoluées par un opérateur
H, et la variance du bruit N additif, blanc et gaussien,
est connue.
Le problème de déconvolution, mal posé,
doit être régularisé. Nous utilisons un modèle
de régularisation introduisant une fonction de potentiel Phi, qui
interdit l'amplification du bruit lors de la restauration tout en
préservant les discontinuités de l'image restaurée,
c'est-à-dire ses contours. Ce modèle admet deux hyperparamètres 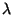 et
et 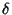 . Nous allons nous intéresser
ici à l'estimation des meilleurs hyperparamètres afin d'effectuer
au mieux la déconvolution, de manière automatique.
Nous proposons pour cela d'utiliser l'estimateur du maximum
de vraisemblance appliqué à l'image observée. Cet
estimateur constitue le critère que nous allons optimiser. Pour
évaluer ses dérivées, nous devons estimer des espérances
calculées sur des échantillons (formant une chaîne
de Markov), qui sont des images dont la probabilité tient compte
des données observées et de l'a priori imposé. Cette
probabilité faisant intervenir l'opérateur de convolution,
il est impossible d'obtenir des échantillons directement par un
échantillonneur. Nous avons développé un algorithme
de type Geman-Yang modifié, utilisant une variable auxiliaire, ainsi
qu'une transformée en cosinus. Nous présentons à cette
occasion un nouvel algorithme de déconvolution, rapide, qui est
dérivé de cette méthode d'échantillonnage.
Nous détaillons ensuite l'algorithme "MCMCML" permettant
d'effectuer simultanément l'estimation des hyperparamètres . Nous allons nous intéresser
ici à l'estimation des meilleurs hyperparamètres afin d'effectuer
au mieux la déconvolution, de manière automatique.
Nous proposons pour cela d'utiliser l'estimateur du maximum
de vraisemblance appliqué à l'image observée. Cet
estimateur constitue le critère que nous allons optimiser. Pour
évaluer ses dérivées, nous devons estimer des espérances
calculées sur des échantillons (formant une chaîne
de Markov), qui sont des images dont la probabilité tient compte
des données observées et de l'a priori imposé. Cette
probabilité faisant intervenir l'opérateur de convolution,
il est impossible d'obtenir des échantillons directement par un
échantillonneur. Nous avons développé un algorithme
de type Geman-Yang modifié, utilisant une variable auxiliaire, ainsi
qu'une transformée en cosinus. Nous présentons à cette
occasion un nouvel algorithme de déconvolution, rapide, qui est
dérivé de cette méthode d'échantillonnage.
Nous détaillons ensuite l'algorithme "MCMCML" permettant
d'effectuer simultanément l'estimation des hyperparamètres 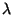 et
et 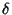 et la restauration
de l'image dégradée. et la restauration
de l'image dégradée.
|