A
b s t r a c t
 Satellite images can be corrupted by an optical blur and electronic
noise, due to the physics of the sensors. The degradation model is
supposed to be known : blurring is modeled by convolution, with a linear operator H,
and the noise is supposed to be additive, white and Gaussian, with a known
variance.
The recovery problem is ill-posed and therefore must be regularized.
We use a regularization model which introduces a Phi function, which avoids
noise amplification while preserving image discontinuities (ie. edges)
of the restored image. This model exhibits two hyperparameters (
Satellite images can be corrupted by an optical blur and electronic
noise, due to the physics of the sensors. The degradation model is
supposed to be known : blurring is modeled by convolution, with a linear operator H,
and the noise is supposed to be additive, white and Gaussian, with a known
variance.
The recovery problem is ill-posed and therefore must be regularized.
We use a regularization model which introduces a Phi function, which avoids
noise amplification while preserving image discontinuities (ie. edges)
of the restored image. This model exhibits two hyperparameters (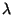 and
and 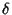 ). Our goal is to estimate
the optimal parameters in order to automatically reconstruct images.
Herein, we propose to use the Maximum Likelihood estimator,
applied to the observed image. To optimize this criterion, we must estimate
expectations by sampling (samples are extracted from a
Markov chain) to evaluate its derivatives. These samples
are images whose probability takes into account the convolution operator.
Thus, it is very difficult to obtain them directly by using a standard
sampler. We have developped a modified Geman-Yang algorithm, using an auxiliary
variable and a cosine transform. We also present a new reconstruction method
based on this sampling algorithm.
Finally, we detail the MCMCML algorithm which enables to simultaneously
estimate ). Our goal is to estimate
the optimal parameters in order to automatically reconstruct images.
Herein, we propose to use the Maximum Likelihood estimator,
applied to the observed image. To optimize this criterion, we must estimate
expectations by sampling (samples are extracted from a
Markov chain) to evaluate its derivatives. These samples
are images whose probability takes into account the convolution operator.
Thus, it is very difficult to obtain them directly by using a standard
sampler. We have developped a modified Geman-Yang algorithm, using an auxiliary
variable and a cosine transform. We also present a new reconstruction method
based on this sampling algorithm.
Finally, we detail the MCMCML algorithm which enables to simultaneously
estimate 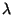 and and 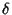 parameters, and to reconstruct the corrupted image.
parameters, and to reconstruct the corrupted image.
|