Validity of Directional Derivatives computed by Automatic Differentiation HOWTO.

Motivation: Automatic Differentiation (AD) tools assume differentiability of the function implemented by the given program. However, due to switches in the control flow, most programs are only piecewise differentiable. Thereby, sometimes the derivatives are wrong, unfortunately this fact is overlook by everyday use of AD. There exist extended models of AD that return useful generalized derivatives for some classes of piecewise differentiable functions, but there is little hope of doing so for all cases. In contrast, our goal is to evaluate, along with the derivative, the size of the differentiable neighborhood around the current input. This ``safe neighborhood" is essential to use the derivatives consistently.

Mechanism: To validate the derivatives we evaluate the interval around the input data where no non-differentiability problem arises. Practically, this requires to analyzing each conditional statement at run-time, in order to find for which data it will switch, and propagate this information as a constraint on the input data.

Requirements:

TAPENADE version 2.1
program to be verify must be Fortran77 (F77) source code.
some F77 compiler.

Procedure:

Once you have your program source code in F77 ready, compile it with the compiler of your choice and run it, all of this just for be sure we're in safe ground.
Define the variables of your interest (dependent and independent).
Call TAPENADE given all the necessary information, any doubts re-read the TAPENADE Tutorial. Instead use the command line option -d (for forward||tangent mode), in order to activate the verification you have to use the option -dV (meaning forward||tangent validity mode).
Add the following line to every subroutine inside your code that should access to the validity information:
```
	
COMMON /validity_test_common/ gmin, gmax, infmin, infmax
REAL gmin, gmax
LOGICAL infmin, infmax 
		
```
That piece of code give you access to the boundaries of the safe neighborhood, where gmin is the lower bound of the interval and gmax is the upper bound, if infmin or infmax is true, then the interval has a infinite lower or upper bound.
Link the following object file validity_test2.o (LINUX-386) to the rest of your binary objects at comiling time.
Compile your code.
Run your program and your're going to get the runtime information about differencial validity.

Example of Application:

Source Code (Simple Piecewise Newton Method).

      PROGRAM main
      REAL tol, x, xd, tmp1, tmp1d
      INTEGER r, it

      tol = 1.0e-3
      r = 0
      x = 6
      WRITE(*, '(/, A, F3.1)') '  Initial guess: ', x
      xd = 1
      WRITE(*, '(A, F3.1)') '  Initial guess direction: ', xd
      it = 20
      WRITE(*, '(A, I4)') '  Iteration times: ', it
      WRITE(*, '(/, A)') "     x       f(x)      f'(x)"
      DO
        CALL F_D( x, xd, tmp1, tmp1d )
        WRITE(*, '(3(F9.5, X))') x, tmp1, tmp1d
C
        x = x - ( tmp1 / tmp1d ) 
        IF ( ABS( tmp1d ) < tol ) EXIT
        r = r + 1
        IF ( r > it ) EXIT
      END DO
      END 

      SUBROUTINE F( x, y ) 
      REAL x, y

      IF ( x > 1 ) THEN
         y = x**2
      ELSE
         y = 2-x**2
      ENDIF
      END

Applying TAPENADE to obtain the derivatives (subroutine F_D )

 > tapenade -d -root F -vars "x" -outvars "y" newton-piecewise.f
   Tapenade - Version 2.1 - (Id: 1.33 vmp Stable - Wed Jan 12 13:35:07 MET 2005) -
     Java 1.5.0_02
   File: (TC33) External procedure f_d is not declared
   @@ Creating ./f_d.f 
   job is completed

 > cat f_d.f
 C        Generated by TAPENADE     (INRIA, Tropics team)
 C  Version 2.1 - (Id: 1.33 vmp Stable - Wed Jan 12 13:35:07 MET 2005)
 C  
 C  Differentiation of f in forward (tangent) mode:
 C   variations  of output variables: y
 C   with respect to input variables: x
 C
      SUBROUTINE F_D(x, xd, y, yd)
      IMPLICIT NONE
      REAL x, xd, y, yd
 C
      IF (x .GT. 1) THEN
        yd = 2*x*xd
        y = x**2
      ELSE
        yd = -(2*x*xd)
        y = 2 - x**2
      END IF
      END

Compiling

 > g77 -c f_d.f
 > g77 f_d.o newton-piecewise.f -o newton-piecewise

Results.

  Initial guess: 6.0
  Initial guess direction: 1.0
  Iteration times:   20

     x       f(x)      f'(x)
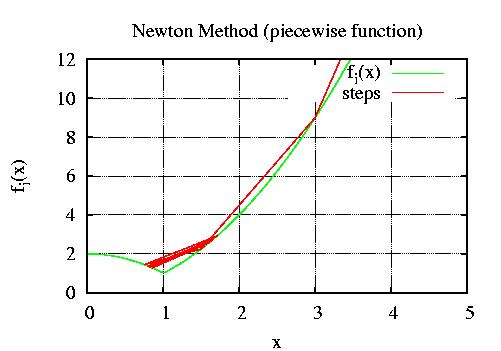
  6.00000  36.00000  12.00000
  3.00000   9.00000   6.00000
  1.50000   2.25000   3.00000
  0.75000   1.43750  -1.50000
  1.70833   2.91840   3.41667
  0.85417   1.27040  -1.70833
  1.59782   2.55301   3.19563
  0.79891   1.36175  -1.59782
  1.65116   2.72634   3.30233
  0.82558   1.31842  -1.65116
  1.62406   2.63756   3.24812
  0.81203   1.34061  -1.62406
  1.63750   2.68140   3.27500
  0.81875   1.32965  -1.63750
  1.63075   2.65935   3.26150
  0.81538   1.33516  -1.63075
  1.63412   2.67034   3.26823
  0.81706   1.33242  -1.63412
  1.63243   2.66483   3.26486
  0.81622   1.33379  -1.63243
  1.63327   2.66758   3.26655

Calling TAPENADE with the validity option (-dV).

 > tapenade -dV -root F -vars "x" -outvars "y" newton-piecewise.f
 Tapenade - Version 2.1 - (Id: 1.33 vmp Stable - Wed Jan 12 13:35:07 MET 2005) -
  Java 1.5.0_02
 File: (TC33) External procedure f_dva is not declared
 @@ Creating ./f_dva.f 
 job is completed

 > cat f_dva.f
 C        Generated by TAPENADE     (INRIA, Tropics team)
 C  Version 2.1 - (Id: 1.33 vmp Stable - Wed Jan 12 13:35:07 MET 2005)
 C  
 C  Differentiation of f in forward (tangent) validated mode:
 C   variations  of output variables: y
 C   with respect to input variables: x
 C
      SUBROUTINE F_DVA(x, xd, y, yd)
      IMPLICIT NONE
      REAL x, xd, y, yd
      yd = 0.0
 C
      CALL VALIDITY_TEST(x - 1, xd)
      IF (x .GT. 1) THEN
        yd = 2*x*xd
        y = x**2
      ELSE
        yd = -(2*x*xd)
        y = 2 - x**2
      END IF
      END

Adding the validity enabling code.

      PROGRAM main
      REAL tol, x, xd, tmp1, tmp1d
      INTEGER r, it
      INTEGER tmp2, tmp3
      COMMON /validity_test_common/ gmin, gmax, infmin, infmax
      REAL gmin, gmax
      LOGICAL infmin, infmax

      tol = 1.0e-3
      r = 0
      x = 6
      WRITE(*, '(/, A, F3.1)') '  Initial guess: ', x
      xd = 1
      WRITE(*, '(A, F3.1)') '  Initial guess direction: ', xd
      it = 20
      WRITE(*, '(A, I4)') '  Iteration times: ', it
      WRITE(*, '(/, A)') "     x       f(x)      f'(x)     gmin      gmax
     +    infmin infmax"
      DO
        gmin=.0
        gmax=.0
        infmin=.TRUE.
        infmax=.TRUE.
        CALL F_DVA(x, xd, tmp1, tmp1d)
        IF ( infmin .eqv. .TRUE. ) THEN 
          tmp2 = 1 
        ELSE 
          tmp2 = 0 
        END IF
        IF ( infmax .eqv. .TRUE. ) THEN 
          tmp3 = 1 
        ELSE 
          tmp3 = 0 
        END IF
        WRITE(*, '(5(F9.5, X), I5, X, I5)') x, tmp1, tmp1d, gmin, gmax 
     +   , tmp2, tmp3
C
        x = x - ( tmp1 / tmp1d )
        IF ( abs( tmp1d ) < tol ) EXIT
        r = r + 1
        IF ( r > it ) EXIT
      END DO
      END 

      SUBROUTINE F( x, y ) 
      REAL x, y

      IF ( x > 1 ) THEN
         y = x**2
      ELSE
         y = 2-x**2
      ENDIF
      END

Validity info.

Compiling

 > g77 -c f_dva.f
 > g77 validity_test2.o f_dva.o newton-piecewise-validity.f -o newton-piecewise-validity

Results

  Initial guess: 6.0
  Initial guess direction: 1.0
  Iteration times:   20

     x       f(x)      f'(x)     gmin      gma    infmin infmax
  6.00000  36.00000  12.00000   5.00000   0.00000     0     1
  3.00000   9.00000   6.00000   2.00000   0.00000     0     1
  1.50000   2.25000   3.00000   0.50000   0.00000     0     1
  0.75000   1.43750  -1.50000   0.00000   0.25000     1     0
  1.70833   2.91840   3.41667   0.70833   0.00000     0     1
  0.85417   1.27040  -1.70833   0.00000   0.14583     1     0
  1.59782   2.55301   3.19563   0.59782   0.00000     0     1
  0.79891   1.36175  -1.59782   0.00000   0.20109     1     0
  1.65116   2.72634   3.30233   0.65116   0.00000     0     1
  0.82558   1.31842  -1.65116   0.00000   0.17442     1     0
  1.62406   2.63756   3.24812   0.62406   0.00000     0     1
  0.81203   1.34061  -1.62406   0.00000   0.18797     1     0
  1.63750   2.68140   3.27500   0.63750   0.00000     0     1
  0.81875   1.32965  -1.63750   0.00000   0.18125     1     0
  1.63075   2.65935   3.26150   0.63075   0.00000     0     1
  0.81538   1.33516  -1.63075   0.00000   0.18462     1     0
  1.63412   2.67034   3.26823   0.63412   0.00000     0     1
  0.81706   1.33242  -1.63412   0.00000   0.18294     1     0
  1.63243   2.66483   3.26486   0.63243   0.00000     0     1
  0.81622   1.33379  -1.63243   0.00000   0.18378     1     0
  1.63327   2.66758   3.26655   0.63327   0.00000     0     1

Interpretation:

For every step we have the validity interval [gmin, gmax] which shows the "safe differential" area around your input. In the present example the problem is point (1.0, 1.0). For instance, the step (3.0, 9.0) has a validity interval [2.0, +inf], which means that on the direccion of derivation (xd=1) there is no problem (+inf), but on the opposite direction we have a problem 2.0 units far from the step.

A second and more appealing example is under development.

Conclusions:

For small an example looks trivial, but for large number of the conditionals the results may be very useful and not easy the obtain using a non-automatic way.

References:

* "Certification of Directional Derivatives Computed by Automatic Differentiation" at The 7th WSEAS International Conference on APPLIED MATHEMATICS (MATH 2005), Cancun, Mexico. May 2005.

* "Domain of Validity of Derivatives Computed by Automatic Differentiation", Rapport de Recherche, RR-5237. INRIA-SOP, France. June 2004.

last update 13/03/2006