Lesson 4: summary

• generic notations and theories
• interfaces and hierarchies
• parametrizing theories
• the BigOp library (the theories of fold)
• subtypes

Let's start with a lie and then make it true:

Generic notations and theories

Polymorphism != overloading.

Example: the == computable equality

We call eqType an interface. With some approximation eqType is defined as follows:

Module Equality.

Structure type : Type := Pack {
  sort : Type;
  op : sort -> sort -> bool;
  axiom : ∀x y, reflect (x = y) (op x y)
}.


End Equality

Interfaces and hierarchies

Mathematical Components defines a hierarchy of interfaces. They group notations and theorems.

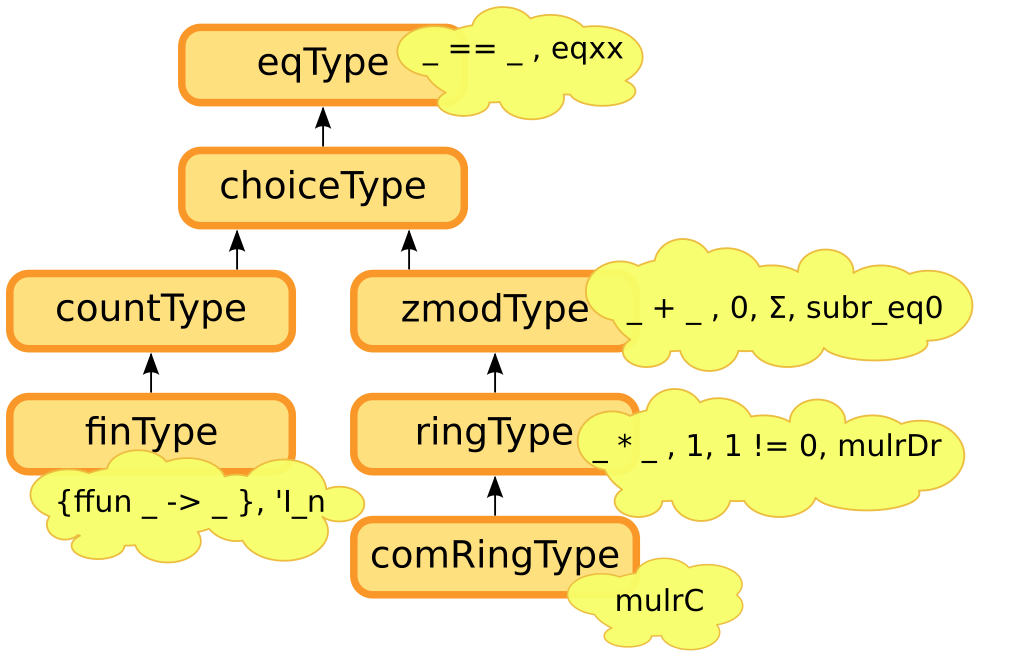
Let's use the theory of eqType

Interfaces do apply to registered, concrete examples such as bool or nat. They can also apply to variables, as long as their type is rich (eqType is richer than Type).

Theories over an interface

Interfaces can be used to parametrize an entire theory

Generic theories: the BigOp library

The BigOp library is the canonical example of a generic theory. It it about the fold iterator we studied in lesson 1, and the many uses it can have.

Most of the lemmas require the operation to be a monoid, some others to be a commutative monoid.

Sub types

A sub type extends another type by adding a property. The new type has a richer theory. The new type inherits the original theory.

Let's define the type of homogeneous tuples

We instrument Coq to automatically promote sequences to tuples.

Now we the tuple type to form an eqType, exactly as seq does.

Which is the expected comparison for tuples?

Given that propositions are expressed (whenever possible) as booleans we can systematically prove that proofs of these properties are irrelevant.

As a consequence we can form subtypes and systematically prove that the projection to the supertype is injective, that means we can craft an eqType.