From mathcomp Require Import all_ssreflect.

Set Implicit Arguments.
Unset Strict Implicit.
Unset Printing Implicit Defensive.

(** 

----------------------------------------------------------
#<div class="slide">#
** Lesson 8: summary

- OOP with mix-ins
- subtypes & automation

Let's remember the truth:

#<div style='color: red; font-size: 150%;'>#
Coq is an object oriented
programming language.
#</div>#


#</div>#
----------------------------------------------------------
#<div class="slide">#
** OOP

# <img style="width: 100%" src="demo-support-master.png"/>#

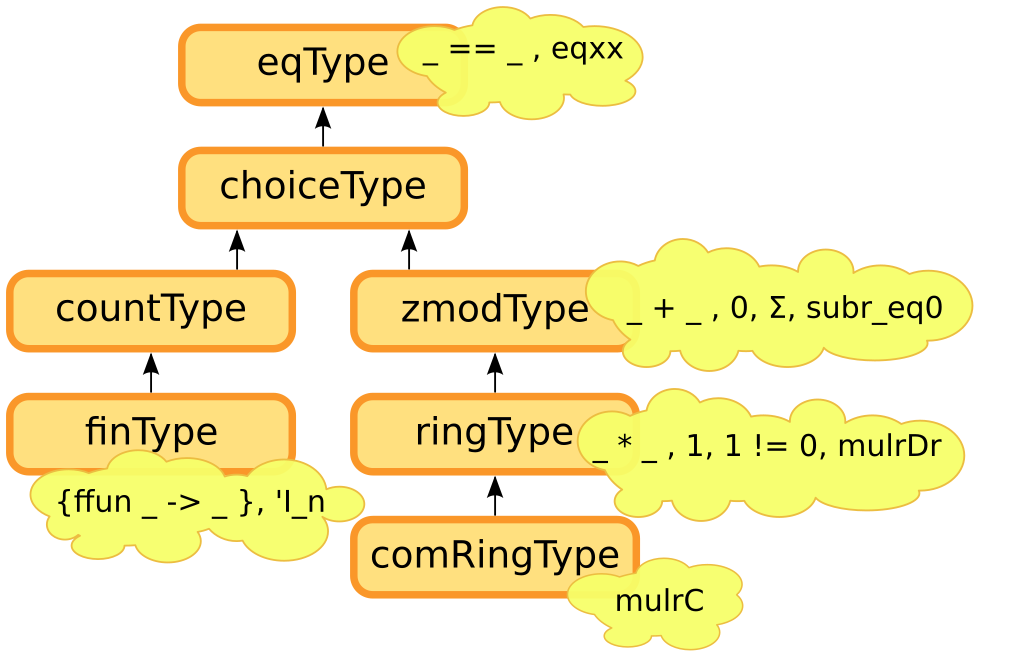
Let's see another interface, the one of finite types

#<div>#
*)

Print Finite.class_of. (* we extend choice with a mix in *)

Print Finite.mixin_of. (* we mix in countable and two specific
                          fields: an enumeration and an axiom *)

Print Finite.axiom.
Print count_mem.

Eval lazy in count_mem 3 [:: 1;2;3;4;3;2;1].

(* The property of finite types is that *)

Check fun (T : eqType) (enum : seq T) =>
        forall x : T, count_mem x enum = 1.

Section Example.

Variable T : finType.

(* Cardinality of a finite type *)
Check #| T |.

(* "bounded" quantification *)
Check [forall x : T, x == x] && false.
Fail Check (forall x : T, x == x) && false.

End Example.


(**
#</div>#


#<div class="note">(notes)<div class="note-text">#
This slide corresponds to
section 6.1 and 6.2 of
#<a href="https://math-comp.github.io/mcb/">the Mathematical Components book</a>#
#</div></div>#

#<p><br/><p>#
#</div>#




----------------------------------------------------------
#<div class="slide">#
** Sub types

A sub type extends another type by adding a property.
The new type has a richer theory.
The new type inherits the original theory.

Let's define the type of homogeneous tuples

#<div>#
*)

Module Tup.

Record tuple_of n T := Tuple {
  tval  :> seq T;
  tsize :  size tval == n
}.
Notation "n .-tuple" := (tuple_of n) : type_scope.

Lemma size_tuple T n (t : n .-tuple T) : size t = n.
Proof. by case: t => s /= /eqP. Qed.

Example seq_on_tuple (n : nat) (t : n .-tuple nat) :
  size (rev [seq 2 * x | x <- rev t]) = size t.
Proof. 
by rewrite map_rev revK size_map.
Undo.
rewrite size_tuple.
Fail rewrite size_tuple.
Abort.


(**
#</div>#

We instrument Coq to automatically promote
sequences to tuples.

#<div>#
*)

Lemma rev_tupleP n A (t : n .-tuple A) : size (rev t) == n.
Proof. by rewrite size_rev size_tuple. Qed.
Canonical rev_tuple n A (t : n .-tuple A) := Tuple (rev_tupleP t).

Lemma map_tupleP n A B (f: A -> B) (t: n .-tuple A) : size (map f t) == n.
Proof. by rewrite size_map size_tuple. Qed.
Canonical map_tuple n A B (f: A -> B) (t: n .-tuple A) := Tuple (map_tupleP f t).

Example seq_on_tuple2 n (t : n .-tuple nat) :
  size (rev [seq 2 * x | x <- rev t]) = size t.
Proof. rewrite size_tuple. rewrite size_tuple. by []. Qed.

(**
#</div>#

Reamrk how [t] is a tuple, then it becomes a list by going
trough rev and map, and is finally "promoted" back to a tuple
by this [Canonical] magic.


Now we the tuple type to form an eqType,
exactly as seq does.

Which is the expected comparison for tuples?

#<div>#
*)

Lemma p1 : size [:: 1;2] == 2. Proof. by []. Qed.
Lemma p2 : size ([:: 1] ++ [::2]) == 2. Proof. by rewrite cat_cons cat0s. Qed.

Definition t1 := {| tval := [::1;2];        tsize := p1 |}.
Definition t2 := {| tval := [::1] ++ [::2]; tsize := p2 |}.

Lemma tuple_uip : t1 = t2.
Proof.
rewrite /t1 /t2. rewrite /=.
Fail by [].
congr (Tuple _).
Fail by [].
(*About bool_irrelevance.*)
apply: bool_irrelevance.
Qed.

(**
#</div>#

Given that propositions are expressed (whenever possible)
as booleans we can systematically prove that proofs
of these properties are irrelevant.

As a consequence we can form subtypes and systematically
prove that the projection to the supertype is injective,
that means we can craft an eqType.

#<div>#
*)


Canonical tuple_subType n T := Eval hnf in [subType for (@tval n T)].
Definition tuple_eqMixin n (T : eqType) := Eval hnf in [eqMixin of n .-tuple T by <:].
Canonical tuple_eqType n (T : eqType) := Eval hnf in EqType (n .-tuple T) (tuple_eqMixin n T).

Check [eqType of 3.-tuple nat].

Example test_eqtype (x y : 3.-tuple nat) : x == y -> True.
Proof.
move=> /eqP H.
Abort.

End Tup.

(**
#<div/>#

Tuples is are part of the library, that also contains
many other "promotions"

#<div>#
*)

Check [finType of 3.-tuple bool].
Fail Check [finType of 3.-tuple nat].

(**
#<div/>#

Tuples is not the only subtype part of the library.
Another one is ['I_n], the finite type of natural
numbers smaller than n.

#<div>#
*)

Print ordinal.
Check [eqType of 'I_3].
Check [finType of 'I_3].

About tnth. (* like the safe nth function for vectors *)

(**
#<div/>#

It is easy to combine these bricks by subtyping (and "specialization")

#<div>#
*)

Check {set 'I_4} : Type.
Check forall a : {set 'I_4}, (a == set0) || (1 < #| a | < 4).
Print set_type.
Check {ffun 'I_4 -> bool} : Type.
Print finfun_type.
Check [eqType of #| 'I_4 | .-tuple bool].
Check [finType of #| 'I_4 | .-tuple bool].

Check {ffun 'I_4 * 'I_6 -> nat} : Type.
Check [eqType of {ffun 'I_4 * 'I_6 -> nat}] : Type.

From mathcomp Require Import all_algebra.
Open Scope ring_scope.

Print matrix.

Section Rings.

Variable R : ringType.

Check forall x : R, x * 1 == x.

Check forall m : 'M[R]_(4,4), m == m * m.

End Rings.

(**
#</div>#

#<div class="note">(notes)<div class="note-text">#
This slide corresponds to
section 6.1 and 6.2 of
#<a href="https://math-comp.github.io/mcb/">the Mathematical Components book</a>#
#</div></div>#

#<p><br/><p>#
#</div>#

----------------------------------------------------------
#<div class="slide">#
** Sum up

- subtypes add properties and inherit the theory of the supertype
  thanks to boolean predicates (UIP).
  In some cases the property can be inferred by Coq, letting one apply
  a lemma about the subtype on terms of the supertype.


#</div>#

*)