From mathcomp Require Import all_ssreflect.

Set Implicit Arguments.
Unset Strict Implicit.
Unset Printing Implicit Defensive.

(** 

----------------------------------------------------------
#<div class="slide">#
** Lesson 7: summary

- generic notations and theories
- interfaces
- parametrizing theories
- the BigOp library (the theories of fold)

Let's start with a lie and then make it true:

#<div style='color: red; font-size: 150%;'>#
Coq is an object oriented
programming language.
#</div>#


#</div>#


----------------------------------------------------------
#<div class="slide">#
** Generic notations and theories

Polymorphism != overloading.

Example: the [==] computable equality

#<div>#
*)


(**
#</div>#

Polymorphism 

#<div>#

*)

Check (_ = _).

Check true = false.

Check (eq true false).

Check @eq.

Check (@eq _ true false).

Check (@eq nat true false).


(**
#</div>#

Overloading : looking inside types 

#<div>#

*)

Check (_ == _).

Check true == false.

Check (@eq_op _ true false).

Check (@eq_op bool_eqType true false).

Check 3 == 4.

Check [::] == [:: 2; 3; 4].

Section T.

Variable T : eqType.
Variable x : T.

Eval lazy in x == x.

End T.

(**
#</div>#

Object oriented flavor

#<div>#

*)

Eval lazy in true == false.

Eval lazy in 3 == 4.

Eval lazy in [::] == [:: 2; 3; 4].

Check (3, true) == (4, false).

Eval lazy in (3, true) == (4, false).

(**
#</div>#

Overloading may fail, polymorphism never

#<div>#

*)

Fail Check (fun x => x) == (fun y => y).

Check (fun x => x) = (fun y => y).

(**
#</div>#

Type inference

#<div>#

*)

Check [eqType of bool].

Fail Check [eqType of bool -> bool].

Check [eqType of {ffun bool -> bool}].

Check [eqType of nat].

Fail Check [eqType of nat -> nat].

Check [eqType of {ffun 'I_256 -> nat}].

Check [eqType of seq nat].

Fail Check [eqType of seq (nat -> nat)].

Check [eqType of seq {ffun 'I_256 -> nat}].

(**
#</div>#

We call [eqType] an interface. With some "approximation"
[eqType] is defined as follows:

<<

Module Equality.

Structure type : Type := Pack {
  sort : Type;
  op : sort -> sort -> bool;
  axiom : ∀x y, reflect (x = y) (op x y)
}.


End Equality
>>

#<div class="note">(notes)<div class="note-text">#
This slide corresponds to
section 5.4 of
#<a href="https://math-comp.github.io/mcb/">the Mathematical Components book</a>#
#</div></div>#
#<p><br/><p>#
#</div>#


----------------------------------------------------------
#<div class="slide">#
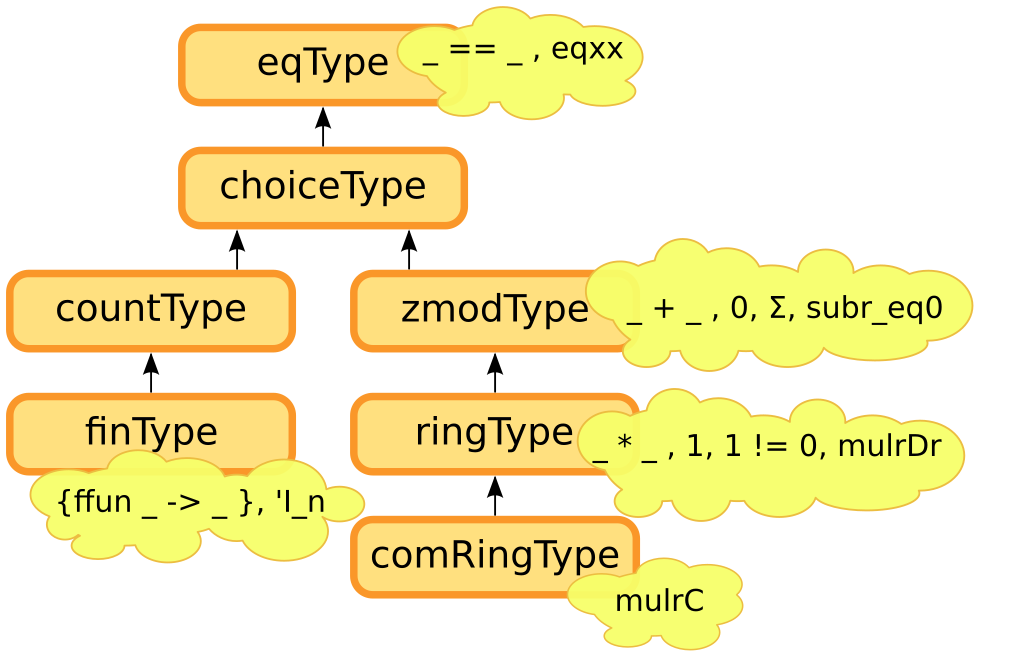
** Interfaces

Mathematical Components defines a hierarchy
of interfaces. They group notations and
theorems.

# <img style="width: 100%" src="demo-support-master.png"/>#

Let's use the theory of [eqType]

#<div>#
*)

About eqxx.

About eq_refl.

Lemma test_eq (*(T : eqType) (x : T)*) :
  (3 == 3) && (true == true) (*&& (x == x)*).
Proof.
rewrite eqxx.
rewrite eqxx.
(* rewrite eqxx. *)
by [].
Qed.

(**
#</div>#

Interfaces do apply to registered, concrete examples
such as [bool] or [nat]. They can also apply to variables,
as long as their type is "rich" ([eqType] is richer than [Type]).

#<div class="note">(notes)<div class="note-text">#
This slide corresponds to
section 5.5 and 7 of
#<a href="https://math-comp.github.io/mcb/">the Mathematical Components book</a>#
#</div></div>#

#<p><br/><p>#
#</div>#


----------------------------------------------------------
#<div class="slide">#
** Theories over an interface

Interfaces can be used to parametrize an
entire theory

#<div>#
*)
Module Seq. Section Theory.

Variable T : eqType.

Implicit Type s : seq T.

Fixpoint mem_seq s x :=
  if s is y :: s1
  then (y == x) || mem_seq s1 x
  else false.

(* the infix \in and \notin are generic, not
   just for sequences. *)

Fixpoint uniq s :=
  if s is x :: s1
  then (x \notin s1) && uniq s1
  else true.

Fixpoint undup s :=
  if s is x :: s1 then
    if x \in s1 then undup s1 else x :: undup s1
  else [::].

End Theory. End Seq.

About undup_uniq.

Eval lazy in (undup [::1;3;1;4]).

Lemma test : uniq (undup [::1;3;1;4]).
Proof.
by rewrite undup_uniq.
Qed.

(**
#</div>#

Others interfaces

**)

Section Interfaces.

Variable chT : choiceType.

Check (@sigW chT).

Check [eqType of chT].

Variable coT : countType.

Check [countType of nat].
Check [choiceType of coT].
Check [choiceType of nat * nat].
Check [choiceType of seq coT].

Variable fT : finType.

Check [finType of bool].
Check [finType of 'I_10].
Check [finType of {ffun 'I_10 -> fT}].
Check [finType of bool * bool].

End Interfaces.


(**
#</div>#

#<div class="note">(notes)<div class="note-text">#
This slide corresponds to
section 5.6 of
#<a href="https://math-comp.github.io/mcb/">the Mathematical Components book</a>#
#</div></div>#

#<p><br/><p>#
#</div>#

----------------------------------------------------------
#<div class="slide">#
** Generic theories: the BigOp library

The BigOp library is the canonical example
of a generic theory. It it about the
[fold] iterator we studied in lesson 1,
and the many uses it can have.

#<div>#
*)

Lemma sum_odd_3 :
  \sum_(0 <= i < 6 | odd i) i = 3^2.
Proof.
rewrite unlock /=.
by [].
Qed.

About big_mkcond.
About big_nat_recr.

Lemma sum_odd_3_bis :
  \sum_(0 <= i < 6 | odd i) i = 3^2.
Proof.
rewrite big_mkcond big_nat_recr //= -big_mkcond /=.
Abort.

Lemma prod_odd_3_bis : (* try [maxn/0] and also [maxn/1] *)
  \big[muln/1]_(0 <= i < 6 | odd i) i = 3^2.
Proof.
rewrite big_mkcond big_nat_recr //= -big_mkcond /=.
Abort.

(**
#</div>#

Most of the lemmas require the operation to be a monoid,
some others to be a commutative monoid.

#<div>#
*)

About bigD1.

(**
#</div>#

Searching for bigop 

#<div>#
*)

Lemma sum_odd_even_all n :
  \sum_(0 <= i < n) i = 
  \sum_(0 <= i < n | odd i) i + \sum_(0 <= i < n | ~~ odd i) i.
Proof.
Search _ (~~ _) in bigop.
by rewrite (bigID odd).
Qed.

(**
#</div>#

Primer for bigop 

#<div>#
*)

Section Primer.

Variable n: nat.
Variable f : 'I_n -> nat.
Variable g : nat -> nat.

Check \big[addn/0]_(i <- [::1; 4; 5] | odd i) g i.

Check \big[addn/0]_(i : 'I_n | odd i) f i.

Definition oddIn := [pred i | odd (i : 'I_n)].

Check \big[addn/0]_(i in oddIn) f i.

Goal \sum_(i in oddIn) i = \sum_(i < n | odd i) i.
Proof.
by [].
Qed.

Check \big[addn/0]_(0 <= i < n | odd i) g i.

Goal \sum_(0 <= i < n | odd i) g i = \sum_(i < n | odd i) g i.
Proof.
Check big_mkord.
rewrite big_mkord.
by [].
Qed.

Goal \sum_(0 <= i < n |odd i) i.*2 = \sum_(0 <= i < n|odd i) (i + i).
Proof.
Fail rewrite addnn.
About eq_bigr.
apply: eq_bigr.
move=> i Hi.
by rewrite addnn.
Qed.

Goal \sum_(0 <= i < n |odd i) i.*2 = \sum_(0 <= i < n | odd i) (i + i).
Proof.
About eq_bigr.
rewrite (eq_bigr (fun i => i + i)) //.
move=> i Hi.
by rewrite addnn.
Qed.

Goal (\sum_(i < n|odd i) i).*2 = \sum_(i < n |odd i) i.*2.
Proof.
About  big_morph.
Fail rewrite big_morph.
rewrite (big_morph _ (_ : {morph double : x y / x + y}) (_ : 0.*2 = 0)).
- by [].
- move=> x y; exact: doubleD.
by [].
Qed.

End Primer.


(**
#</div>#

#<div class="note">(notes)<div class="note-text">#
This slide corresponds to
section 5.7 of
#<a href="https://math-comp.github.io/mcb/">the Mathematical Components book</a>#
#</div></div>#


#<p><br/><p>#
#</div>#

----------------------------------------------------------
#<div class="slide">#
** Sum up

- Coq is an object oriented language ;-)

- in the Mathematical Components library [xxType] is an
  interface (eg [eqType] for types with an equality test).
  Notations and theorems are linked to interfaces.
  Interfaces are organized in hierarchies (we just saw a picture,
  how it works can be found in the book).

#</div>#

*)