

|
Semi-Definite Programming for polynomial constaints
|
Let  and
and 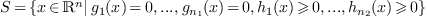 . To solve the
optimization problem
. To solve the
optimization problem
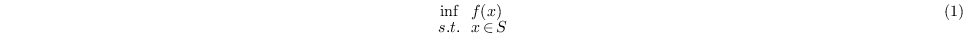
we consider the following (equivalent) problem
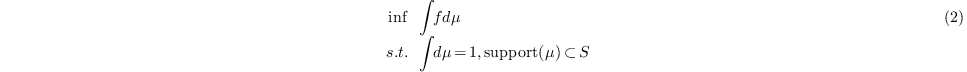
where 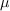 is a positive measure. As any measure
is a positive measure. As any measure
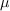 is uniquely determined by its moments:
is uniquely determined by its moments:
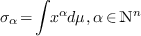
the optimization problem (?) can be replaced by
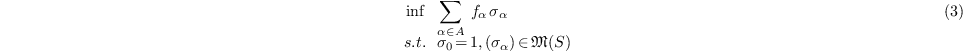
where 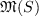 is the cone of moment sequences of
positive measures with a support in
is the cone of moment sequences of
positive measures with a support in  .
.
To have a practical and efficient method to solve this problem, we
truncate the sequence of moments in a given degree and relax the
problem into the optimization of the linear form 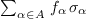 on the cone of matrices of the form
on the cone of matrices of the form
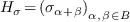
which are semi-definite positive. The condition that the support of
 is in the set
is in the set 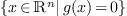 translates as linear conditions on the moments
translates as linear conditions on the moments 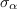 .
The condition that the support of
.
The condition that the support of 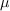 is in the
set
is in the
set 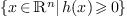 translates into conditions of positivity
on matrices, which entries are linear combinations of the moments
translates into conditions of positivity
on matrices, which entries are linear combinations of the moments 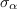 . The truncated relaxation of (?)
leads to the optimization of a linear form on the cone of
semi-definite positive matrices intersected with a linear space. Such
problems can be solved efficiently by interior points method [?].
. The truncated relaxation of (?)
leads to the optimization of a linear form on the cone of
semi-definite positive matrices intersected with a linear space. Such
problems can be solved efficiently by interior points method [?].
The general approach proposed by J.B. Lasserre [?] to solve the polynomial optimization problem (?) consists in solving the Semi-Definite Programming problem truncated moment matrices, degree by degree, until the truncated sequence of moments uniquely characterizes the measure, which is solution of the problem (?).
The method that we use consists in combining the border basis computation, with the Semi-Definite Programming on truncated moment matrices, in order to obtain smaller moment problems and equations defining the minimizer points of (?). More precisely, in each step of the border basis computation, a SDP is solved and a basis of the kernel of the Moment matrix is computed to generate new polynomial equations defining the optimizers until a border basis of the minimizer ideal is computed. A flat extension test [?] is used to check if the moments characterizes a positive measure supported on points. See [?, ?] for more details.
[1] Marta Abril Bucero and Bernard Mourrain. Border Basis relaxation for polynomial optimization. http://hal.inria.fr/hal-00981546, June 2014.
[2] Jean-Bernard Lasserre. Moments, positive polynomials and their applications. Imperial College Press, 2009.
[3] Jean-Bernard Lasserre, Monique Laurent, Bernard Mourrain, Philipp Rostalski, and Philippe Trébuchet. Moment matrices, border bases and real radical computation. Journal of Symbolic Computation, 51:63–85, April 2013.
[4] Monique Laurent and Bernard Mourrain. A Sparse Flat Extension Theorem for Moment Matrices. Archiv der Mathematik, 93:87–98, 2009.
[5] Y. Nesterov and A. Nemirovski. Interior-point polynomial algorithms in convex programming. SIAM, Philaldelphia, 1994.