A case of the direct kinematics of a parallel robot

Given the geometry of a robot and the lengths of its legs, find the different positions  possible (given by a relative position T=[x y z] and an orientation matrix R(q), q=(a,b,c,d), represented with quaternions) .

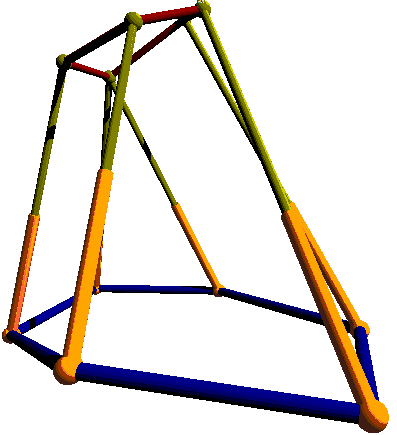
In our case, we consider that two points of attachment of the moving platform are identical, for instance Y1=Y6..

Here is an example of such a robot :

• with 

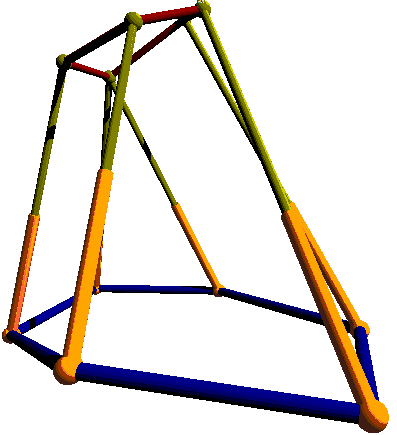
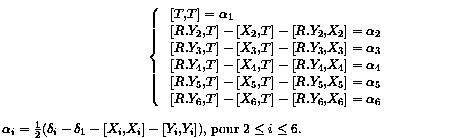
As Y1=Y6, Z1=R.Y1+T is on a circle, so the translation can be written with only one variable, say t for instance. This gives a system of 4 equations which are 4 quadratic forms in (a,b,c,d) .

Then, a system composed by 4 equations, second up fourth, is solved. For this, we construct a resultant matrix for the variables (a,b,c,d) by a generalization of Dixon's method. Its entries are polynomials in one variable t, its determinant is, up to a scalar,  the resultant of these 4 quadratic forms. By computing the eigenvalues and eigenvectors of this matrix we can find the values for t and  q=(a,b,c,d) in the roots of the system. We know  ( you can see...this) we can find at least 40 different solutions.

To know more about all this, see  here  and here

For an example of such a resolution, you can see  one  specialization  and the   moving result .