My name is Viet-Dung Doan - PhD Student , INRIA Sophia Antipolis
Project OASIS - Project TOSCA

2004 Route des Lucioles, BP93, 06902, France
00 33 (0)4 92 38 71 62
Viet_Dung.Doan@sophia.inria.fr

It's me Somewhere in Cote d'Azur
 

My interests :

* Computational Science, Financial Computing Model and Monte Carlo methods.
* Grid Computing, Parallel Algorithmics, Performance Measurement.
* Software Engineering, Distributed - Parallel Applications.

My short bio :

* 10/2006 - 03/2010 (expected) : PhD in Computer Science: Adequation of grid computing to computation intensive calculations in the financial domain.
* 10/2005 - 09/2006 : M.Sc in Computer Science and Applied Mathematic for Finance and Insurance, Ecole Polytech de Nice Sophia Antipolis, France.
* 2004 - 2005 : Software Ingenieur.
* 1999 - 2004 : Bachelor of Science in Computer Science, Hanoi University of Technology, Vietnam.

My current project :

* 01/2006 - 06/2009 ACI-CIGC GCPMF and GRID'5000 research projects.
Computational finance is central to modern financial markets, and an area in which there is a significant amount of commercial and academic interest. To date, grid computing techniques have been applied to this domain.
Subject : Adequation of grid computing to computation intensive calculations in the financial domain
Context
Financial applications require to solve large size computations, that are so huge that they can not be tackled by conventional PCs. A typical example addresses risk analysis evaluation as periodically run by financial institutions (like VaR -- Value at Risk --, and also market risks: greeks, duration, beta, ...). Such risks apply to large sets of financial products (all that are owned or managed by the financial institution), which are very heterogeneous (auctions, contracts, loans, options, etc), and highly parameterized (such as the maturity for options and loans for instance). Moreover, risks depend on external economical factors (as interest rate shocks, currency exchange rates, auctions in specific industrial areas, etc). The use of parallelism is of now and already applied in this financial context, but its usage in Grids is far from being mastered.
PhD Subject
The aim of this PhD research work is to highlight the potential of parallel techniques applied to mathematical finance computing on Grid infrastructures. This should lead to drastic improvements of the risk evaluations at an industrial scale. In order to prove this, the research will specifically focus on computations of volatility and quantiles using Monte Carlo simulation standard techniques, and related more recent techniques for variance calculation or adaptative Monte Carlo simulations (that require much more communications on the Grid than standard Monte Carlo ones). Computing grids are foreseen as a relevant technical solution for computation intensive risk evaluations. But, this requires a mixed approach, adding to classical parallel implementations adequate fault-resilience solutions. The parallelisation of risk evaluation yields a -- possibly quite large -- decomposition into tasks, that subsequently need performant access means to financial databases and dataflows used in those financial calculations. Moreover, those tasks, deployed and running on the Grid, may be demanding regarding synchronization and communication. So, designing a grid-based software platform, able to run financial risk evaluations is really a challenge, that this Doctoral research work's objective is intended to address.
The results of this research will be able to be immediatly given industrial value. Indeed, this research work is lean against a research contract funded by the French Research Agency (ANR), in the Computing Intensive and Grid Computing areas, named GCPMF (Grilles de Calcul appliquées aux Mathématiques Financières). The consortium that conducts this project includes financial institutions and software providers for such institutions. They should be the first to experiment and eventually adopt and apply those research results.
Profile of the candidate
The candidate should be skilled both in mathematical finance, and in computer science (algorithmics, object-oriented programming, distributed software, databases, parallelism and distribution).

My teamwork :

OASIS: Object Actives, Semantic, Internet et Security
TOSCA: TO Simulate and CAlibrate stochastic models.
ProActive : A powerful professional open source middleware for parallel, distributed, multi-threaded programming -> Let's try it !
Francoise Baude: My superviser
Mireille Bossy: My superviser too
Ian Stokes-Rees: An expert in Grid Computing
Stephan Vialle: Professor at Superlec !
Benchmarks of Ian : Grid'5000 benchs 1 Grid'5000 benchs 2

Some simulations :

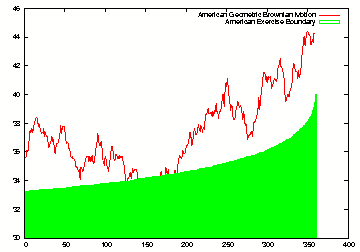Geometric Brownian Motion with exercise boundary 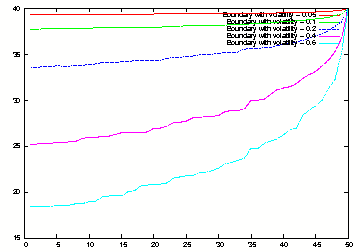Frontier exericise with stochastic volatilities Exercise region above 0 and continuation region below 0 at a random date 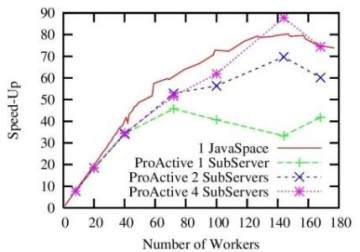Performance
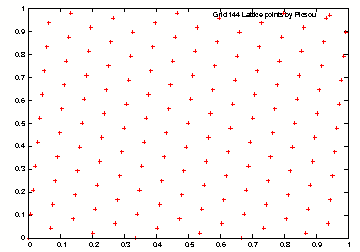Grid 144 lattice points generated in Java in Fortrant by L'ecuyer in Scilab
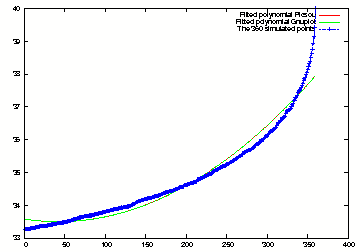Least Square Regression 2th order polynomial 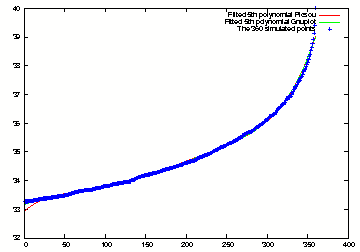Least Square Regression 5th order polynomial Weighted and normal least square regression 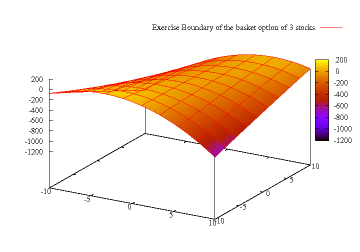Exercise boundary of American Basket Option (3 stocks)

My favor links :

Wilmott - Serving The Quantitative Finance Community - Forums

My papers :

  1. V.D.Doan.Grille de Calcul: Prototypage d'une valorisation d'option européenne et américainne par la méthode de Monte Carlo. Rapport de recherche de Master IMAFA, Ecole Polytechnique de Nice - Sophia Antipolis, September 13, 2006.
  2. S. Bezinne, V. Galtier, S. Vialle, F. Baude, M. Bossy, V. Dung Doan, and L. Henrio. A Fault Tolerant and Multi-Paradigm Grid Architecture for Time Constrained Problems. Application to Option Pricing in Finance. In 2nd IEEE International Conference on e-Science and Grid Computing, December 2006. IEEE Digital Libray -> The slides
  3. V.D. Doan, M. Bossy, F. Baude, and I. Stokes-Rees. Comparison of parallel distributed american option pricing: Though continuation values classification versus optimal exercise boundary computation. In Sixth IMACS Seminar on Monte Carlo Methods (MCM 2007), July. Extented Abstract. Full version accepted to Mathematics and Computers in Simulation Journal, Elsevier, 2010
  4. Viet Dung Doan, Mireille Bossy, Francoise Baude, Abhijeet Gaikwad, and Ian Stokes-Rees. Parallel Pricing Algorithms for Multi–Dimensional Bermudan/American Options using Monte Carlo methods. Research Report 6530, INRIA, 05 2008.http://hal.archives-ouvertes.fr/index.php?halsid=t94knatjn70814eglnlfhnfs73&view_this_doc=inria-00278514&version=2
  5. I. Stokes-Rees, F. Baude, V.D. Doan, and M. Bossy. Managing parallel and distributed monte carlo simulations for computational finance in a grid environment. In Simon Lin, editor, Proceedings of the International Symposium on Grid Computing 2007. Springer Verlag, 2008.
  6. V.D. Doan, A. Gaikwad, M. Bossy, and F. Baude. “Gridifying” classification-monte carlo algorithm for pricing high-dimensional american options. In Workshop on High Performance Computational Finance, IEEE/ACM Supercomputing 2008, November 2008, IEEE Xplore http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=4745402&isnumber=4745391
  7. A. Gaikwad, V.D. Doan,M. Bossy, F. Abergel, F. Baude SuperQuant Financial-Benchmark Suite for Performance Analysis of Grid Middlewares In 4th International Conference on High Performance Scientific Computing, Modeling, Simulation and Optimization of Complex Processes, Extended Abstract , March 2009. Full paper under review for inclusion in the final proceedings. Also available as Tech. Report INRIA 2009 http://hal.archives-ouvertes.fr/index.php?halsid=t94knatjn70814eglnlfhnfs73&view_this_doc=inria-00387324&version=2
  8. -> Picazo