


Next: L'analyse complexe et l'équation
Up: Approximation rationnelle et méromorphe
Previous: Approximation rationnelle et méromorphe
Posons quelques notations préliminaires.
Soient
-
-
 le disque unité.
le disque unité.
-
-
 le cercle unité.
le cercle unité.
Pour tout polynôme
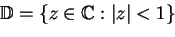 |
(5.1) |
à coefficients complexes, on notera son polynôme réciproque
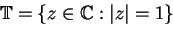 |
(5.2) |
On designera par
 l'espace des fonctions continues sur
l'espace des fonctions continues sur
 à valeurs complexes.
à valeurs complexes.
Dans la mesure où nous allons principalement travailler dans le
disque unité, on notera dans la suite
 ,
l'espace de Hilbert usuel des fonctions f(z) Lebesgue mesurables
à valeurs complexes sur
,
l'espace de Hilbert usuel des fonctions f(z) Lebesgue mesurables
à valeurs complexes sur
 telles que
telles que
 |
(5.3) |
muni du produit scalaire usuel
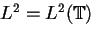 |
(5.4) |
De même, on désignera par
 l'espace de Banach
l'espace de Banach
 des fonctions f(z) à valeurs complexes
essentiellement bornées sur
des fonctions f(z) à valeurs complexes
essentiellement bornées sur
 muni de la norme
muni de la norme
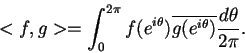 |
(5.5) |
En notant la décomposition de Fourier de la fonction f comme
 |
(5.6) |
on posera
 la fonction
la fonction
 |
(5.7) |
On définira aussi Hp (p=2 ou  )
comme le sous-espace fermé
de Lp suivant :
)
comme le sous-espace fermé
de Lp suivant :
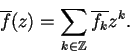 |
(5.8) |
Il est un résultat bien connu [50, ch. 13] que toute
fonction f de H2 s'étend de manière analytique à
 ,
ce
qui est aussi valable pour
,
ce
qui est aussi valable pour  puisque
puisque
 ;
Notons la caractérisation équivalente suivante :
;
Notons la caractérisation équivalente suivante :
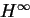 |
(5.9) |
et la trace de f sur le cercle unité
 est alors obtenue comme
limite non tangentielle presque partout.
Il est également classique que toute fonction f non nulle de l'espace
de Hardy H2 se décompose de manière unique en f=jw où
est alors obtenue comme
limite non tangentielle presque partout.
Il est également classique que toute fonction f non nulle de l'espace
de Hardy H2 se décompose de manière unique en f=jw où
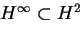 |
(5.10) |
appartient à H2 et est appelé le facteur extérieur de fcependant que
 est de module 1 presque partout sur
est de module 1 presque partout sur
 et s'appelle le facteur intérieur de f. Ce dernier peut lui-même
se décomposer en j=bS où
et s'appelle le facteur intérieur de f. Ce dernier peut lui-même
se décomposer en j=bS où
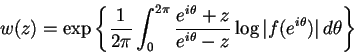 |
(5.11) |
est le produit de Blaschke avec un zéro d'ordre k à l'origine
associé à la suite de points
 et à la
constante
et à la
constante
 ,
cependant que
,
cependant que
 |
(5.12) |
est le facteur singulier associé à la mesure positive  qui est
singulière par rapport à la mesure de Lebesgue.
Les zl sont bien sûr les zéros de
qui est
singulière par rapport à la mesure de Lebesgue.
Les zl sont bien sûr les zéros de  comptés avec leur
multiplicité. S'il y en a une infinité, la convergence de bdans
comptés avec leur
multiplicité. S'il y en a une infinité, la convergence de bdans
 est assurée par la condition
est assurée par la condition
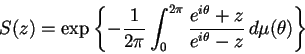 |
(5.13) |
qui résulte automatiquement du fait que
 .
Lorsque
f est analytique à travers le disque
.
Lorsque
f est analytique à travers le disque
 ,
,
 est nulle et S vaut
identiquement 1 (cf. [46,30]).
est nulle et S vaut
identiquement 1 (cf. [46,30]).
On notera par ailleurs
 le complémentaire orthogonal
de H2 dans L2 et l'on notera
le complémentaire orthogonal
de H2 dans L2 et l'on notera
 l'opérateur de
projection sur
l'opérateur de
projection sur
 ,
ainsi que
,
ainsi que
 la projection sur H2.
la projection sur H2.
Enfin, pour p=2 ou  ,
on désignera par HpN l'espace
Hp + RN, où RN est l'espaces des fractions rationnelles de
degré au plus N et ayant tous leurs pôles dans
,
on désignera par HpN l'espace
Hp + RN, où RN est l'espaces des fractions rationnelles de
degré au plus N et ayant tous leurs pôles dans
 et s'annulant
à l'infini (donc
et s'annulant
à l'infini (donc
 ).
).



Next: L'analyse complexe et l'équation
Up: Approximation rationnelle et méromorphe
Previous: Approximation rationnelle et méromorphe
Frederic Mandrea
2001-01-21
 l'espace des fonctions continues sur
l'espace des fonctions continues sur
 à valeurs complexes.
à valeurs complexes.
 telles que
telles que
 des fonctions f(z) à valeurs complexes
essentiellement bornées sur
des fonctions f(z) à valeurs complexes
essentiellement bornées sur
 muni de la norme
muni de la norme
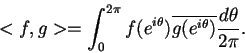
 la fonction
la fonction

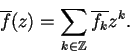
 est alors obtenue comme
limite non tangentielle presque partout.
Il est également classique que toute fonction f non nulle de l'espace
de Hardy H2 se décompose de manière unique en f=jw où
est alors obtenue comme
limite non tangentielle presque partout.
Il est également classique que toute fonction f non nulle de l'espace
de Hardy H2 se décompose de manière unique en f=jw où
 est de module 1 presque partout sur
est de module 1 presque partout sur
 et s'appelle le facteur intérieur de f. Ce dernier peut lui-même
se décomposer en j=bS où
et s'appelle le facteur intérieur de f. Ce dernier peut lui-même
se décomposer en j=bS où
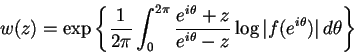
 ,
cependant que
,
cependant que
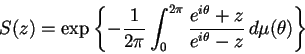
 ,
,
 le complémentaire orthogonal
de H2 dans L2 et l'on notera
le complémentaire orthogonal
de H2 dans L2 et l'on notera
 ,
ainsi que
,
ainsi que