La page "Présentation" de l'INRIA

Mécanismes spatiaux

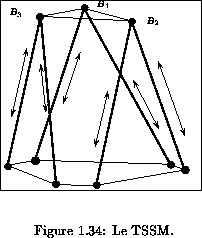
Nous considérons maintenant le cas des mécanismes spatiaux. Nous adoptons une démarche similaire à celle utilisée pour le cas des mécanismes planaires. On va limiter notre étude à un cas particulier d'un robot que nous appellons TSSM, représenté en figure 1.34.

Pour un TSSM dont les longueurs de segment sont fixées considérons les triangles formés par un point d'articulation du mobile et les deux points d'articulation correspondants sur la base. Pour ces faces triangulaires le seul mouvement possible est une rotation autour de la droite passant par les points d'articulation de la base. En conséquence les points d'articulation du mobile se trouveront sur des cercles dont le centre se trouve sur la droite.

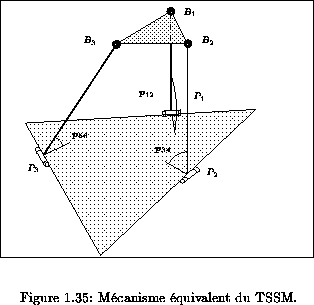
Les coordonnées des centres des cercles et leurs rayons peuvent s'exprimer facilement en fonction des longueurs des segments. On peut donc construire un mécanisme équivalent du TSSM constitué de trois segments dont une extrémité tourne autour d'une articulation rotode et dont l'autre extrémité est articulée sur le plateau mobile (figure 1.35).

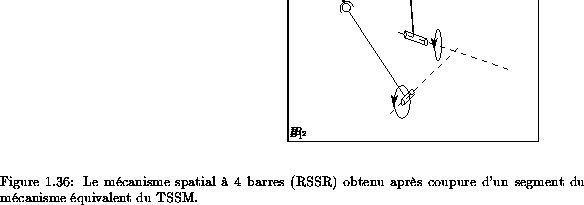
On détache un des segments du plateau mobile mécanisme équivalent du TSSM et l'on considère le reste du mécanisme. On obtient un mécanisme spatial à 4 barres (figure 1.36), constitué de 4 segments reliés par deux articulations rotodes à axe concourant et de deux rotules. Ce mécanisme est désigné sous le nom générique de RSSR, quelle que soit la position des axes des articulations rotodes.

Il est connu que le point , de coordonnées (), de ce mécanisme se trouve sur une surface d'ordre 16. Si l'on considère maintenant le nombre de points d'intersection de cette surface avec le cercle décrit par l'extrémité du segment équivalent que nous avons détaché, on obtient le nombre de modes d'assemblage possible pour le mécanisme étudié. Une surface d'ordre 16 coupe un cercle en un maximum de 32 points. Mais parmi ces points, certains vont se trouver sur la sphère imaginaire: ils doivent donc être décomptés du nombre 32. Il est possible d'établir que la circularité du RSSR est de 8 ce qui impose qu'au moins 16 points d'intersection sont imaginaires. Un majorant du nombre de mode d'assemblage est donc 16. Il est même possible de montrer que le nombre de solution réelle sera paire et qu'il y aura au plus 2 solutions convexes.

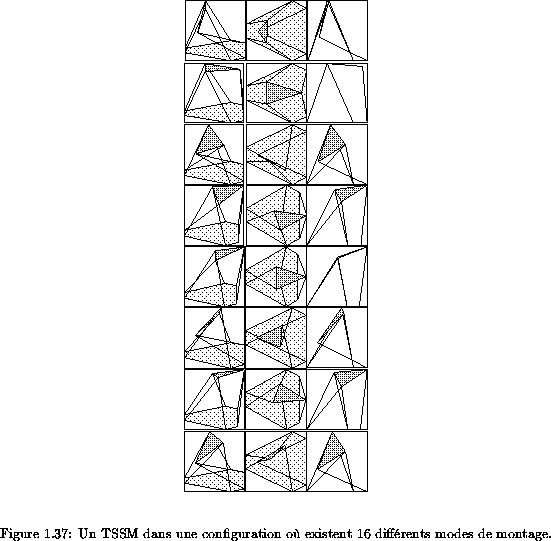
A partir des équations du mécanisme équivalent il est possible de ramener le problème à la résolution d'un polynôme mono-variable de degré 16 et, par une procédure numérique, de trouver effectivement 16 solutions réelles.

Un exemple à 16 configurations est représenté sur la figure 1.37.