La page "Présentation" de l'INRIA

Mécanisme plan

Dans ce cas le système des équations de la cinématique inverse fournit 3 équations non-linéaires qu'il s'agit de résoudre pour trouver la solution de la cinématique directe: on perçoit alors que ce problème sera difficile.

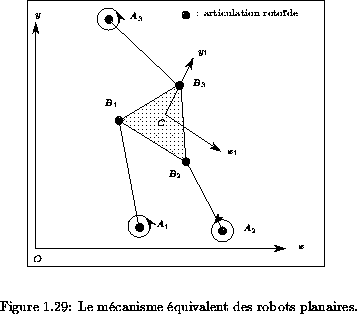
La démarche que nous adoptons consiste tout d'abord à montrer que la solution du problème n'est pas unique, c'est-à-dire qu'il existe plusieurs modes d'assemblage de ce manipulateur, en se basant uniquement sur des considérations géométriques. Pour les deux architectures de robots planaires on fixe donc les variables articulaires et l'on obtient le mécanisme décrit dans la figure 1.29, que l'on va appeler le mécanisme équivalent des robots planaires.

Pour tenter d'estimer a priori le nombre de modes d'assemblage, nous examinons un sous-mécanisme obtenu à partir du mécanisme équivalent en désolidarisant un des points d'articulation du plateau mobile de son segment.

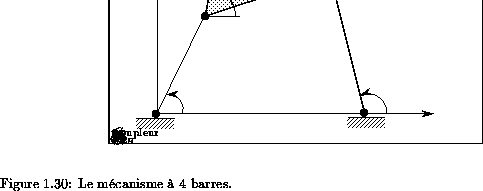
Le mécanisme obtenu, connu sous le nom de mécanisme à 4 barres est décrit en figure 1.30: il n'est composé que d'articulations rotodes, les longueurs de ses segments sont fixées et il possède un degré de liberté.

Ce mécanisme est constitué de 4 barres articulées 1, 2, 3, 4; à la barre 3 est rigidement lié un corps que nous appellerons le coupleur, dont la géométrie est définie par les longueurs et l'angle . Le reste du mécanisme est défini par les longueurs des barres 1, 2, 4, soit , et par deux angles : l'angle entre les barres 1 et 2 et l'angle entre les barres 1 et 4. Si l'on fait varier l'un de ces angles chaque point du coupleur ( par exemple) décrit une courbe que nous appellerons courbe de coupleur. Pour ce type de mécanisme on sait que cette courbe est forcément algébrique. Pour le robot parallèle le point se trouve aussi sur le cercle décrit par l'extrémité du segment que nous avons désolidarisé. Les positions possibles de ce point se trouvent donc à l'intersection des deux courbes, ce qui implique que leur nombre sera fini, en général.

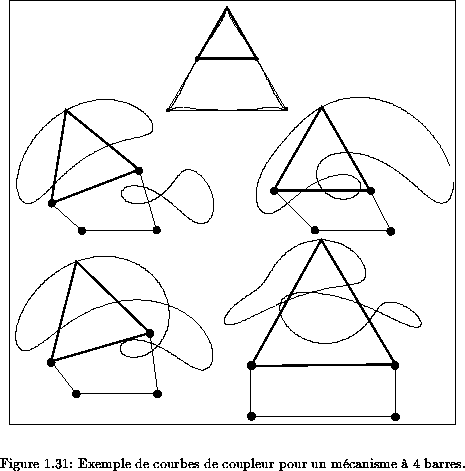
Nous supposons qu'un moteur entra^ne en rotation le segment 2, modifiant ainsi l'angle du mécanisme et nous nous intéressons aux déplacements du point , de coordonnées (), du coupleur. Il est bien connu que ce point décrit une sextique (la figure 1.31 illustre quelques exemples de courbes de coupleur).

Cette sextique a une propriété particulièrement intéressante pour notre étude : elle est tricirculaire, c'est-à-dire qu'elle a trois points doubles sur le cercle imaginaire.

Faisons un rappel de certaines notions sur les intersections des courbes algébriques, qui nous seront très utiles par la suite. Une courbe algébrique de degré coupe une courbe algébrique de degré en général en points. Ce résultat, bien connu, peut sembler paradoxal si on l'applique aux cercles : il conduirait à l'existence de 4 points d'intersection. Ce paradoxe s'explique d'une manière simple que nous rappelons pour mémoire.

Considérons l'équation d'un cercle, dont les coordonnées du centre sont (), de rayon : que l'on réécrit, en introduisant un nouveau terme, sous la forme : Le terme est simplement un facteur d'échelle. L'équation précédente est dite homogène puisque on peut l'écrire sous la forme: où tous les termes sont maintenant de degré 2 dans les variables . Le système est alors appelé un système de coordonnées planes homogènes. La ligne définie par doit couper le cercle en deux points, dont les coordonnées satisfont l'équation:

c'est-à-dire aux points , définis par : Ces deux points imaginaires sont appelés les points circulaires imaginaires et l'équation (1.8) définit le cercle imaginaire. Puisque les termes n'interviennent pas dans les coordonnées des points circulaires imaginaires tous les cercles du plan les contiennent. Donc l'intersection de deux cercles quelconques contiendra toujours les deux points circulaires imaginaires et, par conséquent, deux cercles ne peuvent se couper en plus de deux points réels.

Si une courbe du plan contient les points comme point double, triple.... on dira alors que cette courbe a une circularité de 2, 3...

Revenant à notre sextique , le terme tricirculaire signifie simplement que sa circularité est de 3. En effet (voir [8]) l'équation de la sextique exprimée en coordonnées homogènes s'écrit pour :

ce qui, en dehors du cas où le quadrilatère est un triangle, se ramène à :

La sextique contient donc les points comme points triples. Remarquons aussi que la circularité de cette courbe est maximale, puisqu'une sextique ne peut avoir une circularité supérieure à 3.

Si l'on considère le mécanisme défini en figure 1.29 et que l'on désaccouple le segment le reste du mécanisme devient un mécanisme à 4 barres articulées. Le nombre de points d'intersection de la courbe du coupleur avec le cercle de centre et de rayon donne alors le nombre de montage possible. Or la courbe décrite par est une sextique que l'on coupe par un cercle : le nombre de points d'intersection est donc de 12 au maximum. Toutefois les points , vu la tricircularité de la sextique, vont compter pour 6 points d'intersection. On peut donc affirmer qu'il existe au plus 6 montages possibles pour ce type de robot parallèle.

A partir de l'équation de la sextique on peut obtenir une équation polynomiale mono-variable qui permet effectivement de trouver des configurations à six solutions.

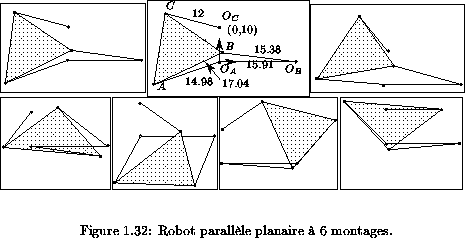
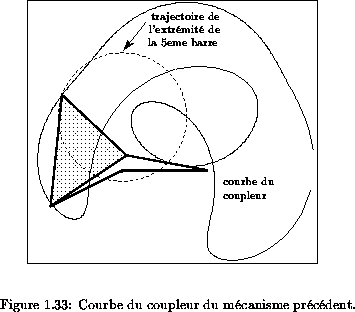
La figure 1.32 montre un robot parallèle présentant le nombre maximum de montages possibles et la figure 1.33 le tracé de la courbe du coupleur du mécanisme à 4 barres associé, ce qui permet de constater visuellement la présence de 6 points d'intersection entre la courbe du coupleur et le cercle décrit par l'extrémité du segment dissocié.