Les poignets
Nous avons vu que l'organe terminal d'un manipulateur aura en général 3
degrés de liberté en rotation. Du point de vue de l'espace atteignable
on désirera une étendue comparable à celle du poignet humain (ce qui
permet par exemple d'utiliser quasiment les mêmes outils). Se référant
à l'architecture du poignet humain on peut se rendre compte qu'il se
comporte grossièrement comme une rotule. Les axes de rotation sont donc
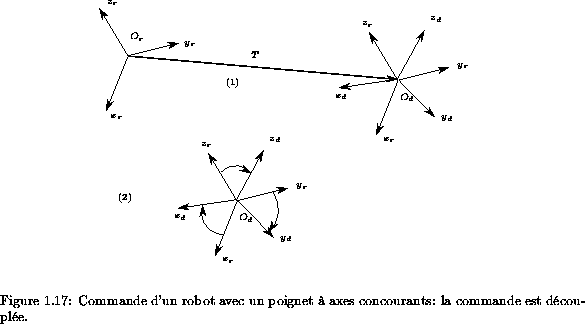
concourants. Ceci présente l'avantage majeur de découpler la commande du
manipulateur. En effet le problème de commande se ramène à faire
concider deux repères , le repère du robot dans sa position
courante et
le repère de consigne. En utilisant les 3 premiers
degrés de liberté du porteur on peut faire concider facilement
avec
, puis procéder aux rotations autour de
pour faire
concider les axes des repères (figure 1.17).
Dans le problème classique de
cinématique inverse
où l'on désire déterminer les
coordonnées articulaires à partir des coordonnées généralisées
on découpe ainsi un système global de 6 équations à 6 inconnues
non-linéaire en deux systèmes de dimension 3 beaucoup plus facile à
résoudre. Dans le cas où les axes de rotation du poignet ne sont pas
concourants mais en position quelconque il est possible alors de montrer que
le problème de la cinématique inverse peut se ramener à la
résolution d'un polynôme mono-variable de degré 16.
Ces considérations expliquent pourquoi, dans la très grosse majorité
des cas, les poignets des robots industriels sont à axes concourants.
On va diviser ces poignets en deux catégories: la plus courante est celle
des poignets avec roulis, tanguage et lacet (axes des rotations tous
perpendiculaires entre eux)
et la deuxième est du type
roulis, tanguage, roulis (axes des rotations non perpendiculaires)
(figure 1.18).
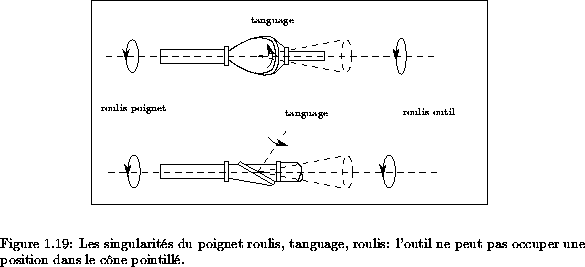
La deuxième solution présente l'intérêt d'avoir un espace
atteignable en général plus important mais l'inconvénient de
présenter une singularité lorsque les deux axes de roulis sont
alignés: dans ce cas l'outil ne peut pas évoluer dans un cône
(figure 1.19).
Next: Robots en cha^ne Up: Robot en cha^ne Previous: Les robots à